Способы представления двоичных чисел

В современных цифровых системах числа обычно представляются в двоичной системе счисления, основанием которой является число 2. При этом целое k - разрядное десятичное число записывается виде n- разрядного двоичного числа, где

=0, 1, … , 9 – цифра в i-том разряде десятичного числа;

= 0 или 1 – цифра в j–ом разряде 2-го числа.

Введением отрицательных степеней числа 2 представляются дробные числа.

Т.о. в двоичной системе счисления любое число можно представить двумя цифрами : 0 и 1. Для представления этих чисел используются схемы, которые могут принимать 2 состояние, четко различающиеся знанием какой-либо электрической величины – напряжения или тока. Одному из значений соответствуют “0”, другому - “1”.

Целые и действительные числа могут иметь 2 формы представления

• С правеющей запятой;

• С фиксированной запятой.

При использовании плавающей запятой число состоит из 2 частей: мантиссы (m), которая содержит значащие цифры числа, и порядка (p), который показывает степень, в которую надо возвести основание системы счисления (q), чтобы полученное при этом число умноженное на мантиссу, давало истинное значение представленного числа:

=m·q^p

Обычно число дается в нормализованном виде, когда его мантисса является правильной дробью, причем первое значащая цифра (“1”) следует сразу после запятой.

При использовании фиксированной запятой число представляется в виде единого целого, причем положение запятой в используемой разрядной сетке жестко фиксировано.

Цифровые системы, использующие числа с плавающей запятой сложнее, чем использующие числа с фиксированной запятой, так как при этом, требуется выполнение операций как над мантиссами так и над порядками. Однако диапазон представляемых чисел при одинаковом числе разрядов в системах с плавающей запятой значительно больше.

Для представления знака числа используется дополнительный знаковый разряд Z, который обычно располагается перед числовыми разрядами. Для дополнительных чисел значение знакового разряда Z=0, для отрицательных чисел Z=1. Для чисел с плавающей запятой вводятся отрицательные знаковые разряды для мантиссы и для порядка чисел.

Основы алгебры-логики и выполнение логических операций

Теоретической основой проектирования цифровых систем является алгебра-логика или булевая алгебра . В алгебре-логике различные логические выражения могут иметь только 2 значения – “истинно” (обозначатся “1”) или “ложно” (обозначатся “0”). Это условие называется законом “исключенного третьего”.

В общем случае логические выражения является функциями логических переменных X₁, X₂,…. Х_k, каждая из которых может иметь значения 0 или 1. Если есть k-логических переменных, то они образуют 2^k возможных логических наборов из 0 и 1. Для каждого набора переменных логическая функция F может принимать значения 0 или 1. Поэтому для k-переменных можно образовать различных логических функций.

Все возможные логические функции k-переменных можно образовать с помощью трех основных операций:

• Логическое отрицание (инверсия, операция НЕ) обозначается ^— над переменными;

• Логическое сложение (дизъюнкция, операция ИЛИ) обозначается + , V;

• Логическое умножение (конъюнкция , операция И ) обозначается • , Λ, &;

Таблица истинности операции инверсии

A	F = Ā
0	1
1	0

Таблица истинности операций дизъюнкции и конъюнкции

A	B	F = A + B	F = A • B
0	0	0	0
0	1	1	0
1	0	1	0
1	1	1	1

Для рассмотренных логических операций справедливый ряд аксиом (тождеств) и законов:

Аксиомы	1 + А = 1 0 • А = 0
	0 + А = А 1 • А = А
	А + А = А А • А = А
	А + Ā = 1 А • Ā = 0
	= А
Законы коммутативности (переместительный)	А + В = В + А А • В = В • А
Законы ассоциативности (сочетательный)	А + В + С = А + (В + С) А • В • С = А • (В • С)
Законы дистрибутивности	А • (В + С) = (А • В) + (А • С) А + (В • С) = (А + В)• (А + С)
Законы дуальности (теоремы де-Моргана)	= Ā • = Ā +
Законы поглощения	А + А • В = А А• (А + В) = А

Применение данных тождеств и законов позволяет производить упрощение логических функций, таким образом сводя к минимальному количеству конечных элементов, необходимых для реализации магических функций.

Используя законы ассоциативности, любую логическую функцию многих переменных (k>2) можно предоставить в виде комбинаций функций двух переменных. Для 2 переменных существует полный набор из 16 логических функций 2 переменных. Каждая функция обозначает одну из 16 возможных логических операций, имеет собственное название и обозначение.

Логические функции могут иметь различные формы предоставления:

• словесное;

• табличное;

• алгебраическое;

• графическое.

1. Пример словесного описания для F₉= f(A,B).

F₉=1, когда значения переменных A=B и F₉=0, когда A≠B

2. Эту функцию можно предоставить в виде следующей таблицы истинности, которая содержит все 2^k возможных наборов значений логических переменных и значении функции, соответствующие каждому из наборов.

   А	В	F9
   0	0	1
   0	1	0
   1	0	0
   1	1	1

3. Чтобы осуществить переход от табличного представления к алгебраическому, каждому набору переменных ставиться в соответствие минтерм (конституанта единицы) – конъюнкция всех переменных, которые входят в прямом виде, если значения данной переменной в наборе равно 1, либо в инверсном виде, если значение переменной равно 0.

Для k переменных составляется q=2^k минтермов: m₀, m₁,…,m_q-1 .

Значения функции F, соответствующие согласно таблице истинности данному i-му набору переменных, обозначим ƒ_i

A	B	Минтермы	Макстермы	Значение функции F9
0	0	m0 = Ā •	М0 = Ā +	ƒ0 = 1
0	1	m1 = Ā •B	М1 = Ā + В	ƒ1 = 0
1	0	m2 = A•	М2 = А +	ƒ2 = 0
1	1	m3 = A•B	М3 = А + В	ƒ3 =1

В общем случае алгебраическое выражение любой логической функции можно представить в следующем виде:

ƒ_i – значение функции (0 или 1)

m_i – минтерм, соответствующие i-му набору переменных. Такое представление функции называется ее совершенной дизъюнктивной нормальной формой (СДНФ).

Для функции =f₀m₀ + f₁m₁+ f₂m₂+ f₃m₃ = 1• (Ā • ) + 0• (Ā •B) + 0• (A• ) +1• (A•B)= Ā +AB

Другая алгебраическая форма представления функции получается при изменении макстермов (конституанта 0) – это дизъюнкция всех переменных, которые входят в прямом виде, если значения е данной переменной равно 1, либо в инверсном виде, если значение переменной равно 0. Число макстермов для функции k переменных равно q=2^k. Алгебраическое выражение функции получается в виде произведения: 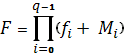, где ƒ_i и М_i - значение функции и минтерм, соответствующие i-му набору переменных.

Такое представлении функции называется ее совершенной конъюнктивной нормальной формой(СКНФ).

Для функции =(f₀ + M₀) • (f₁ + M₁) • (f₂ + M₂) • (f₃ + M₃) = (1+ Ā + ) • (0 + Ā + B) • (0 + A + ) • (1 + A+ B)= (Ā + ) • (A + )

Таким образом любая логическая функция может быть представлена в в идее СДНФ или СКНФ. Используя логические тождества и законы, можно получить их них более простые формы представления функции, которые называются минимизированными .

4. При относительно небольшом числе переменных (k≤6) удобным и наглядным является графическое представление логических функций в виде карт минтермов. Наиболее распространенной их формой является карты Карно.

Карта Карно содержит q=2^k клеток, причем каждой клетке соответствует один из q элементов.

Для F₉= Ā +AB

A B	0	1
0	Ā	A
1	Ā B	AB

A B	0	1
0	1
1		1

Для F= Ā + Ā C + A + ABC

AB C	00	01	11	10
0	1			1
1	1		1

AB C	00	01	11	10
0	Ā	Ā C	AB	A
1	Ā C	Ā BC	ABC	A C

Чтобы представить на карте Карно логическую функцию, заданную в виде СДНФ, то в клетках, соответствующих минтермам, входящим в СДНФ, ставиться 1. Остальные клетки остаются незаполненными или заполняются 0.

Рассмотренные функции имеют определенное значение ƒ_i =0 или ƒ_i =1, при всех возможных наборах логических переменны. Такие логические функции называются полностью определенными.

Кроме них есть функции, значение которых определено только для части логических наборов переменны. Эти функции называются частично определенными.

Наборы переменных, для которых функция определенна, называются рабочими, а для которых не определена называются безразличными. Значение функции соответствующие безразличным наборам, обозначается в таблицах истинности и на картах Карно “Х”.

Частично определенную функцию можно сделать полностью определенной (доопределить), приписав безразличными наборам какие-либо значения функции ƒ_i =0 или ƒ_i =1. Доопределенные функции производится так, чтобы упростить ее алгебраическое выражение и практическую реализацию.

Логическую функцию большого числа переменных можно представить в виде композиции функции меньшого числа переменных.

F(x₁, x₂, … , x_n) = F₀(0, x₂, … , x_n)+ x₁F₁(0, x₂, … , x_n)

Процесс выделения более простых составляющих функций называется декомпозицией. Полученные функции F₀ и F_1, могут подвергаться дополнительной декомпозиции.

Итак, любую логическую функцию можно представить в виде СДНФ или СКНФ, то есть с помощью соответствующей комбинации простейших логических функций И, ИЛИ, НЕ. Набор простейших функций с помощью которого можно выразить любые другие, сколь угодно сложных логические функции, называются функционально-полными или логическим базисом.

То есть набор функций И, ИЛИ, НЕ являются одним из логических базисов.

Логический базис называется минимальным, если удаленная, хотя бы одной из входящих в него функции, превращают этот набор в функциональный неполный. С помощью знаков дуальности из логического базиса И, ИЛИ, НЕ можно исключить функцию И либо ИЛИ.

В результате получаем минимальные логические базисы, содержащие только одну функцию и штрих Шеффера (И-ИЛИ); стрелка Пирса (ИЛИ-НЕ).

Электронные схемы, выполняющие простейшие логические операции называются логическими элементами. Для реализации в цифровых схемах разнообразных логических функций достаточно иметь логические элементы, реализующие операции того или иного минимального базиса. Этот набор логических элементов называется минимальным элементным базисом (или базой). В современной микроэлектронике таким образом чаще всего служат элементы И-НЕ либо ИЛИ-НЕ.