Питання для самостійного вивчення.

_{1.Частотні характеристики рядів розподілу.}

_{2.Характеристики центру розподілу.}

_{3.Характеристики розміру та ступеня варіації.}

_{4.Характеристики форми розподілу.}

_{Література:  2 - 11}

Методичні рекомендації

_{Ряд розподілу характеризує склад, структуру сукупності за певною ознакою. Елементами ряду розподілу є варіанти - значення ознаки та частоти . Залежно від статистичної природи варіантів ряди поділяються на атрибутивні та варіаційні. У співвідношенні варіантів та частот проявляється закономірність розподілу. Вона описується низкою статистичних характеристик, зокрема:}

_{а) частотні характеристики;}

_{б) характеристики центру розподілу;}

_{в) характеристики варіації;}

_{г) характеристики нерівномірності розподілу, концентрації, асиметрії.}

_{Частотними характеристиками будь-якого ряду є абсолютна чисельність j-ї групи – частота та відносна частота - частка .}

_{Очевидно, що , а або 100%.}

_{Додатковою характеристикою варіаційних рядів є кумулятивна частота (частка ), яка характеризує обсяг сукупності із значеннями варіант, які не перевищують ,. Кумулятивні частотні характеристики утворюються послідовним підсумовуванням абсолютних частот. Так, , , і т.д. якщо інтервали варіаційного ряду нерівні, то використовують щільність (густину) частоти (частки) на одиницю інтервалу або де - ширина j-го інтервалу.}

_{В інтервальних рядах, припускаючи рівномірний розподіл у межах j-го інтервалу, як варіант використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою ж, як і сусіднього закритого інтервалу.}

_{До характеристик центру розподілу відносять середню, моду та медіану.}

_{Мода - це найпоширеніше значення ознаки, тобто варіанта, яка в ряду розподілу має найбільшу частоту (частку).}

_{У дискретному ряду визначається візуально за максимальною частотою, або часткою. В інтервальному ряду за найбільшою частотою визначається модальний інтервал. Конкретне значення моди в інтервалі}

_{обчислюється за формою:}

_,

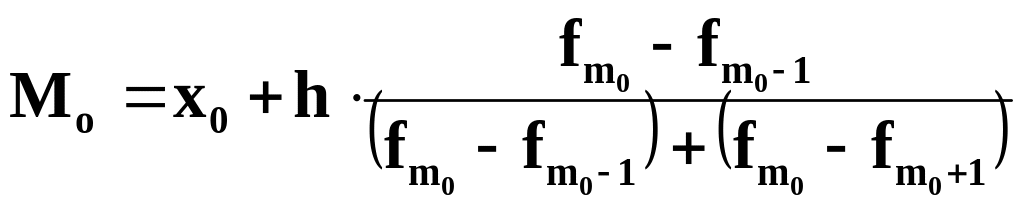_{де та – відповідно нижня межа та ширина модального інтервалу,}

_{, , - частоти (частки) модального, передмодального та післямодального інтервалу.}

_{Медіана – це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини. Медіана, як і мода, не залежить від крайніх варіант, тому застосовується для характеристика центру в ряду розподілу з невизначеними межами. Для визначення , у ряду використовують кумулятивні частоти або частки . У дискретному ряду медіаною буде значення ознаки, для якої кумулятивна частота перевищує половину обсягу сукупності 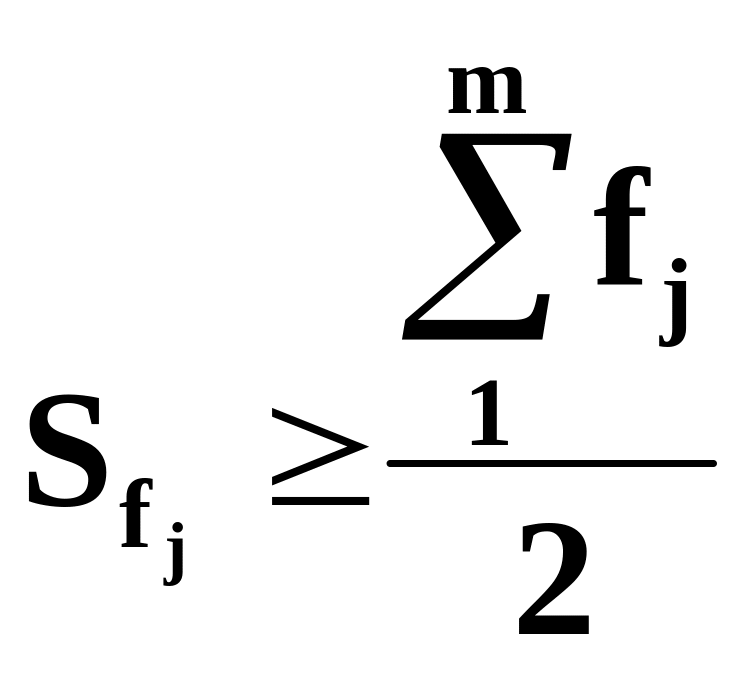, або кумулятивна частка . В інтервальному ряду у такий спосіб визначається медіанний інтервал. Конкретне значення медіани в інтервалі обчислюється за формулою:}

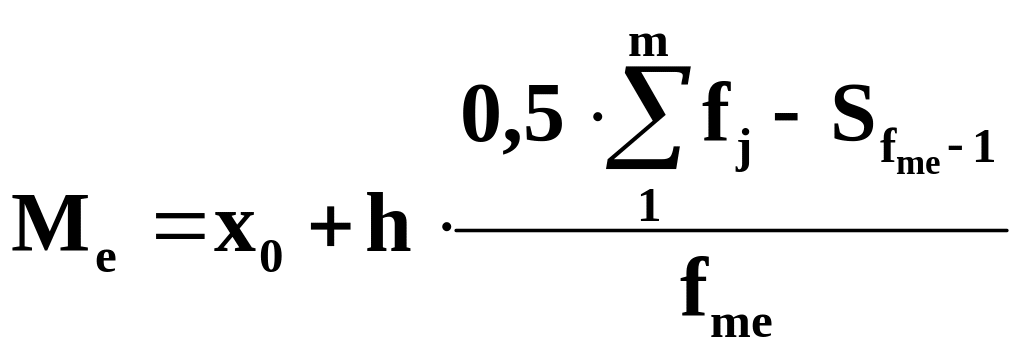
_{де та - відповідно нижня межа та ширина медіанного інтервалу;}

_{- частота медіанного інтервалу;}

_{- кумулятивна частота передмедіанного інтервалу.}

_{У симетричних рядах розподілу значення моди та медіани збігаються з середньою величиною , а в помірно асиметричних вони співвідносяться таким чином: .}

_{Для вимірювання та оцінки варіації використовують абсолютні та відносні характеристики. До абсолютних відноситься: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії; відносні характеристики представлені низкою коефіцієнтів варіації, нерівномірності, локалізації концентрації.}

_{Варіаційний розмах характеризує діапазон варіації, це різниця між максимальним і мінімальним значенням ознаки:}

_.

_{Якщо крайні значення ознаки не типові для сукупності, то використовують квартильні або децільні розмахи. Квартальний розмах охоплює 50% обсягу сукупності, та визначається по формулі:}

_.

_{Децильний розмах можна визначати так:}

_{, .}

_{Узагальнюючою мірою варіації є середнє відхилення індивідуальних значень ознаки від центру розподілу. Оскільки алгебраїчна сума відхилень , то в розрахунках використовують або модулі , або квадрати відхилень.}

_{Середній з модулів відхилень називають середнім лінійним відхиленням ; середній квадрат відхилень - дисперсією а, корінь квадратний з дисперсії - середнім квадратичним відхиленням :}

_{; .}

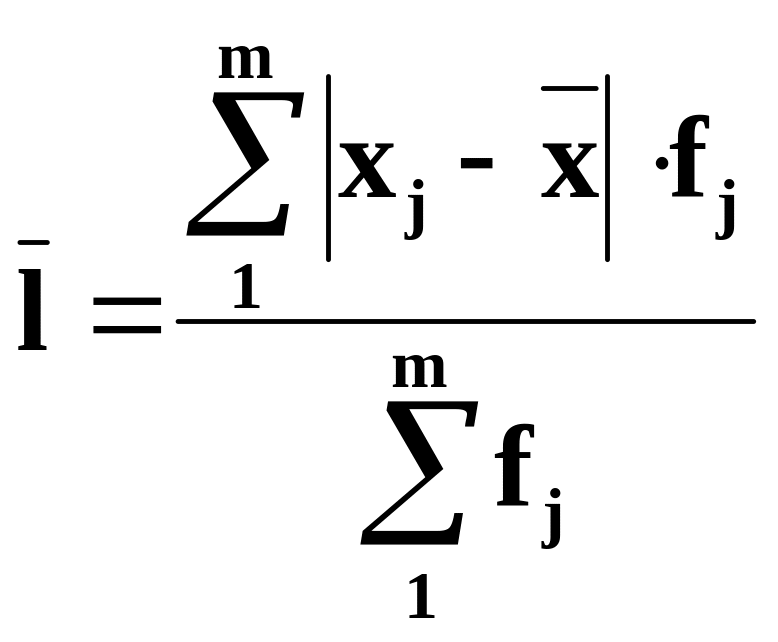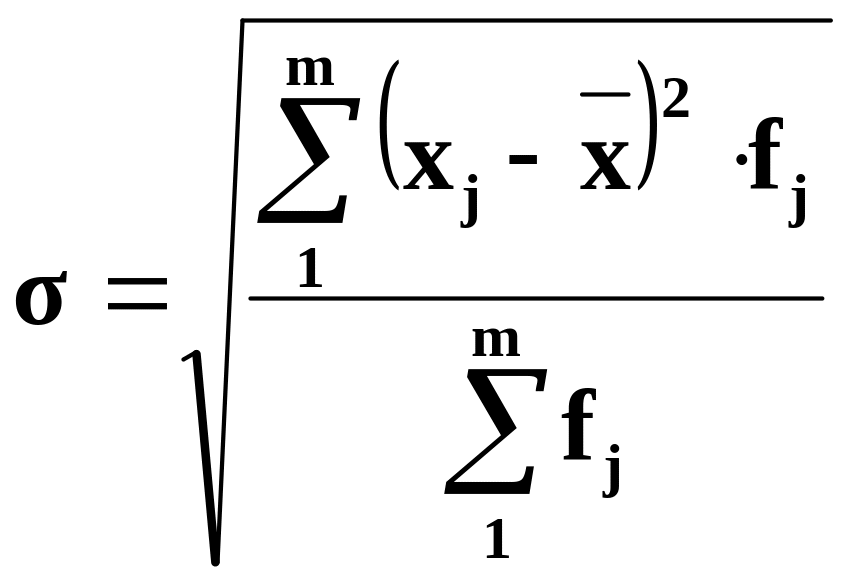_{За первинними, не згрупованими даними наведені характеристики варіації розраховуються за принципом незваженої середньої, тобто:}

_{; .}

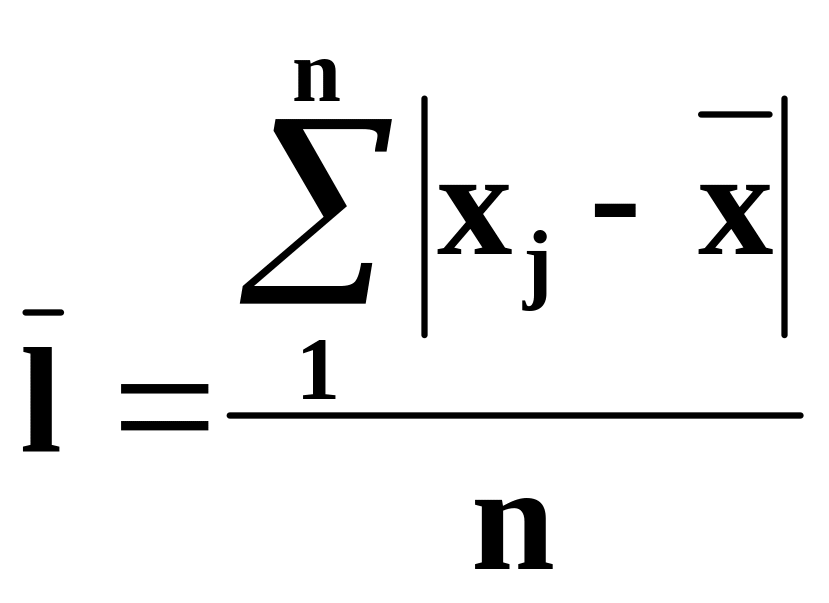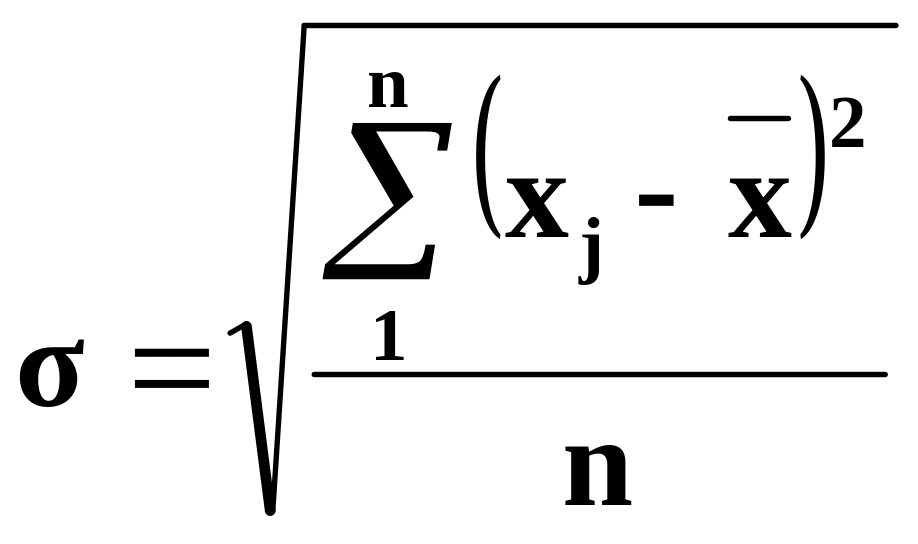_{Середнє лінійне та середнє квадратичне відхилення:}

_{- іменовані числа (в одиницях вимірювання ознаки);}

_{- за змістом ідентичні, проте через математичні властивості . У симетричному, близькому до нормального, розподілі , .}

_{Дисперсію використовують не лише для оцінки варіації, а й при вимірюванні взаємозв'язків, для перевірки статистичних гіпотез тощо. Для ознак метричної шкали розрахунок дисперсії ведеться за формулами}

_.

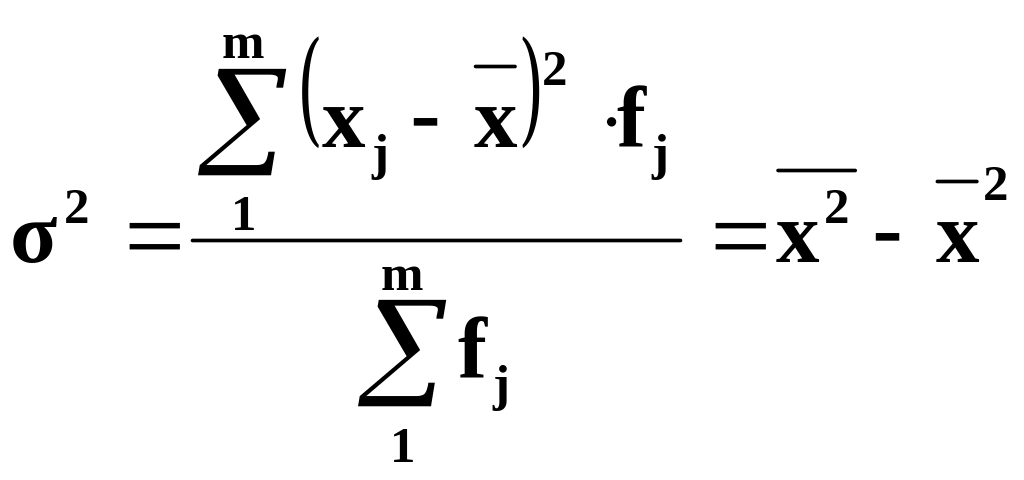_{Як і будь-яка середня, дисперсія має певні математичні власності:}

_{а) якщо всі значення ознаки зменшити (збільшити) на певну величину, дисперсія не зміниться;}

_{б) якщо всі значення ознаки змінити в К разів, то дисперсія зміниться в К2 разів;}

_{в) у разі заміни частот частками дисперсія не зміниться.}

_{Для альтернативної ознаки, варіація якої має два взаємовиключні значення - "1" та "0", а розподіл характеризується відповідно двома частками – та , дисперсія розраховується як добуток часток .}

_{Порівнюючи варіації різних ознак або однієї ознаки у різних сукупностях, використовують відносні характеристики варіації. Коефіцієнти варіації розраховуються як відношення абсолютних, іменованих характеристик варіації ( , , ) до центру розподілу і часто виражаються процентами, отже:}

_{1) лінійний коефіцієнт варіації ;}

_{2) квадратичний коефіцієнт варіації ;}

_{3) коефіцієнт осциляції .}

_{Квадратичний коефіцієнт варіації використовують – як критерій однорідності сукупності. У симетричному, близькому до нормального, розподілі . Розрізняють такі значення відносних коливань:}

_{- – незначне коливання;}

_{- – середнє коливання;}

_{- – велике коливання.}