Вимоги до оформлення роботи

Звіт по лабораторній роботі повинен містити:

1. Титульний аркуш.

2. Аркуш із завданням.

3. Використовувані розрахункові формули з коментарями.

4. Проміжні й фінальні результати розрахунків.

5. Аналіз результатів.

6. Висновки по роботі.

Контрольні питання до захисту лабораторної роботи

1. Причини виникнення надмірності й методи боротьби з нею.

2. Теорема Шеннона для дискретного каналу без перешкод і її фізичний зміст.

3. Теоретичні основи й методики побудови статистичних кодів Шеннона-Фано й Хаффмена.

4. Алгоритми стиску даних (арифметичне кодування, словникові методи кодування, кодування довжин повторень, диференціальне кодування).

Лабораторна робота №3 розрахунок інформаційних характеристик безперервних повідомлень. Дискретизація сигналів

Мета роботи: навчиться робити оцінку інформаційних характеристик безперервних повідомлень і каналів зв'язку, а також коректно підбирати параметри АЦП при перекладі безперервного сигналу в цифровий.

Задачі роботи:

1. Вивчити властивості й метод оцінки диференціальної ентропії безперервних повідомлень.

2. Вивчити властивості й методи оцінки (-ентропії безперервних повідомлень.

3. Вивчити способи оцінки інформаційних параметрів аналогових каналів зв'язку.

4. Вивчити умови узгодження інформаційних характеристик джерел безперервних повідомлень і аналогових каналів зв'язку.

5. Вивчити способи розрахунку параметрів АЦП.

Загальні положення

У даній лабораторній роботі будуть розглядатися джерела безперервних сообщений, які в кожний момент часу можуть випадковим образом прийняти одне з нескінченної множини можливих станів. Під безперервним повідомленням будемо розуміти деяку безперервну випадкову величину, що однозначно відповідає стану джерела. Імовірнісний опис такого повідомлення X задається його щільністю розподілу w(x).

Для опису інформаційних властивостей безперервних величин уведені наступні величини: диференціальна ентропія й  (эпсилон) ентропія.

Диференціальна ентропія не є мірою власної інформації, що втримується в ансамблі значень випадкової величини Х. Вона залежить від масштабу Х и може приймати негативні значення. Інформаційний зміст має не сама диференціальна ентропія, а різниця двох диференціальних энтропій, чим і пояснюється її назва.

-ентропія визначає мінімальну кількість інформації, що втримується в одному відліку безперервного повідомлення для відтворення його із заданою вірністю.

Вихідні дані для лабораторної роботи наведені в таблиці 3.1:

• щільність імовірності миттєвих значень первинного сигналу ;

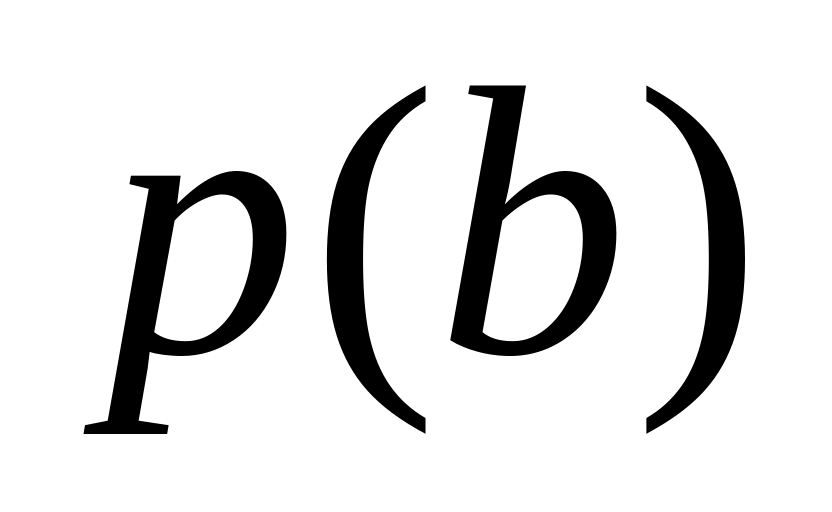• середня потужність сигналу 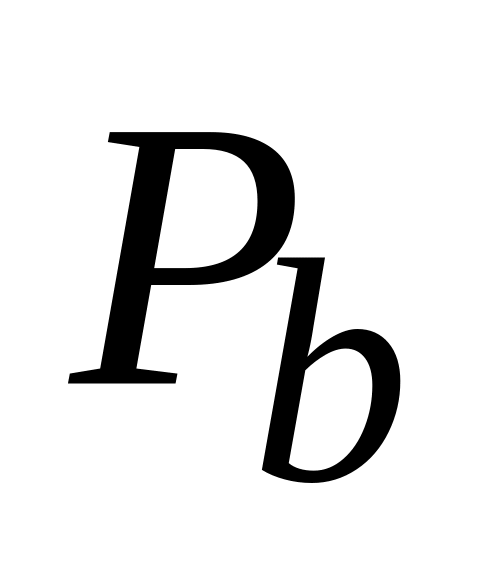,Вт;

• коефіцієнт амплітуди 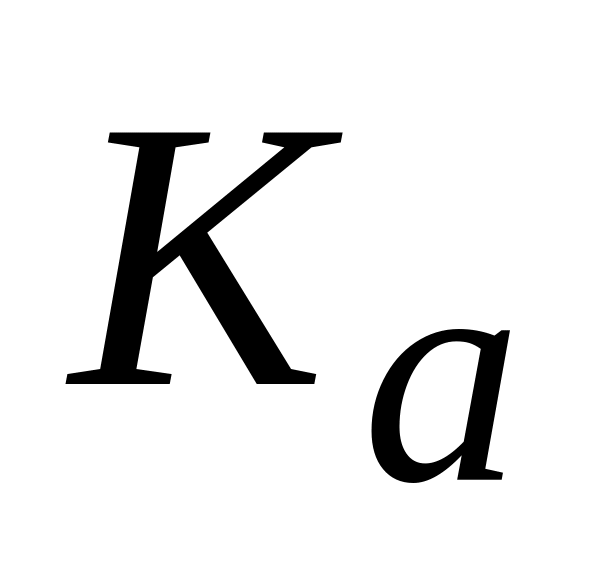первинного сигналу;

• максимальна частота спектра первинного сигналу ;

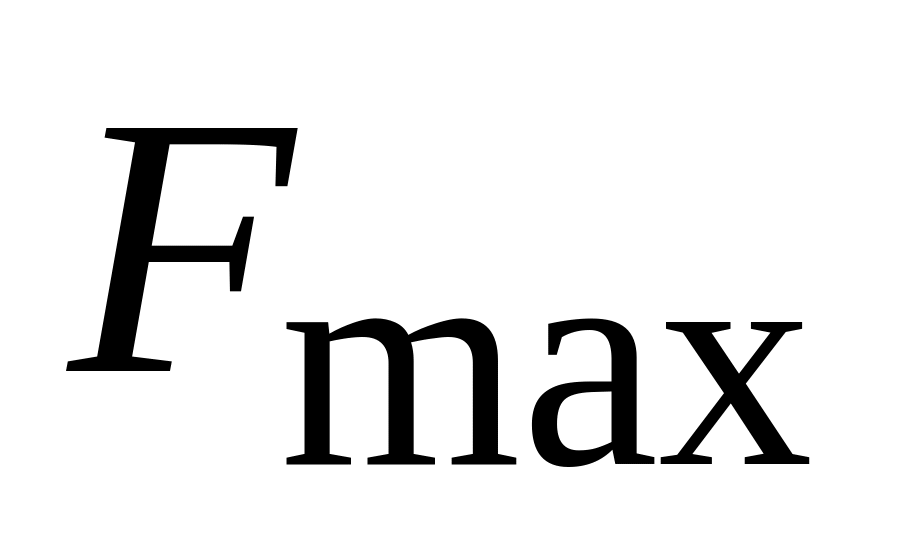• відношення середньої потужності первинного сигналу до середньої потужності помилки відтворення на виході системи передачі ;

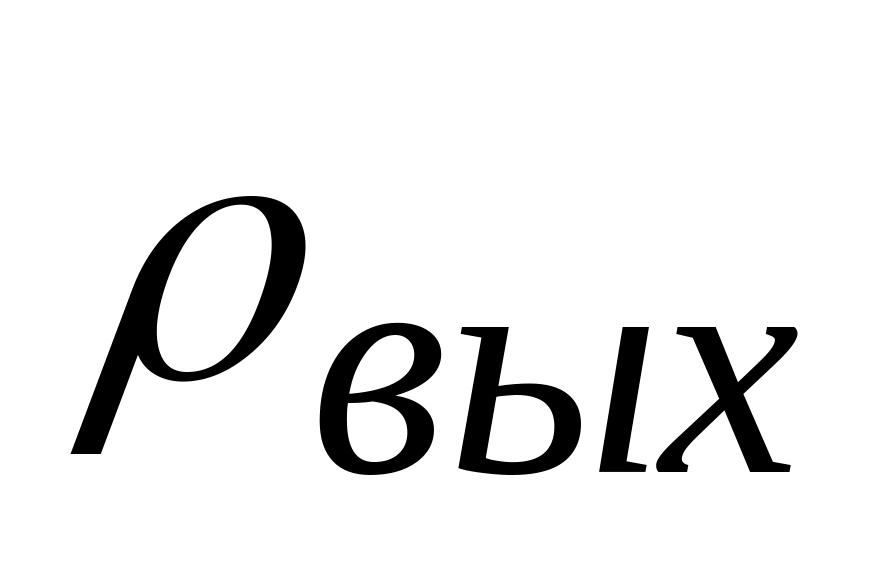• відношення сигнал/шум квантування .

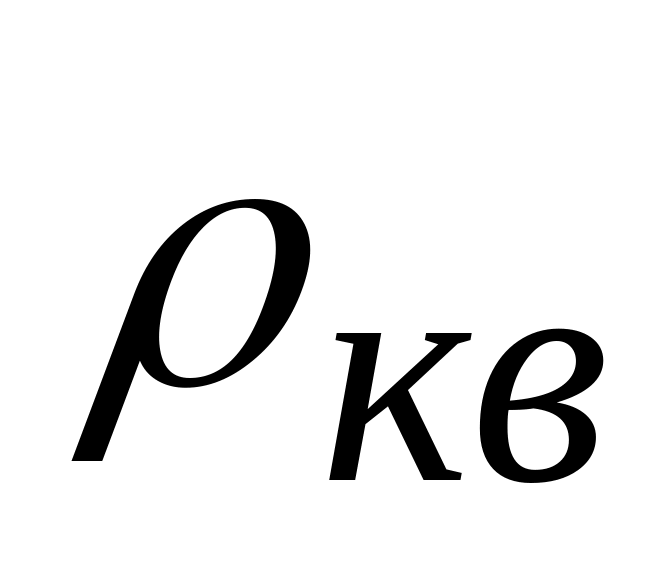Частина 1. Розрахунок інформаційних характеристик джерела безперервних повідомлень

Повідомлення безперервного джерела перетвориться в первинний аналоговий сигнал звичайно без втрати інформації, тому розрахунки інформаційних характеристик джерела проводяться для первинного сигналу.

Підлягають розрахунку:

• диференціальна ентропія джерела ;

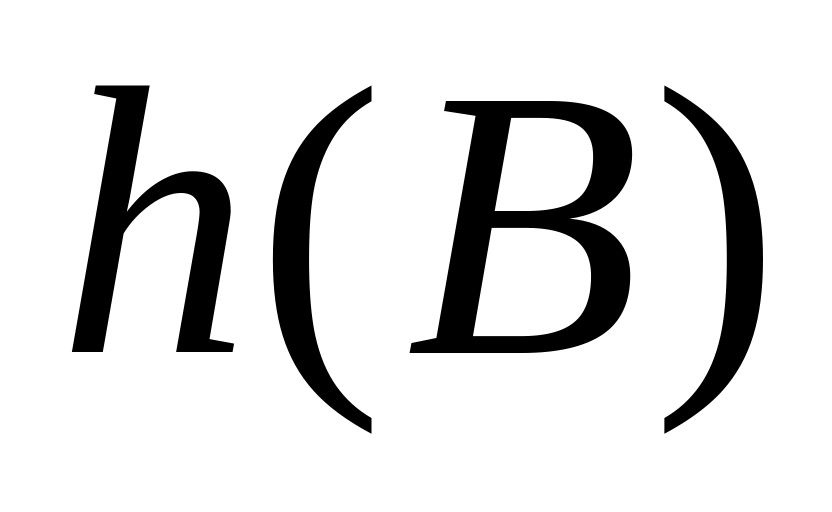• умовна диференціальна ентропія ;

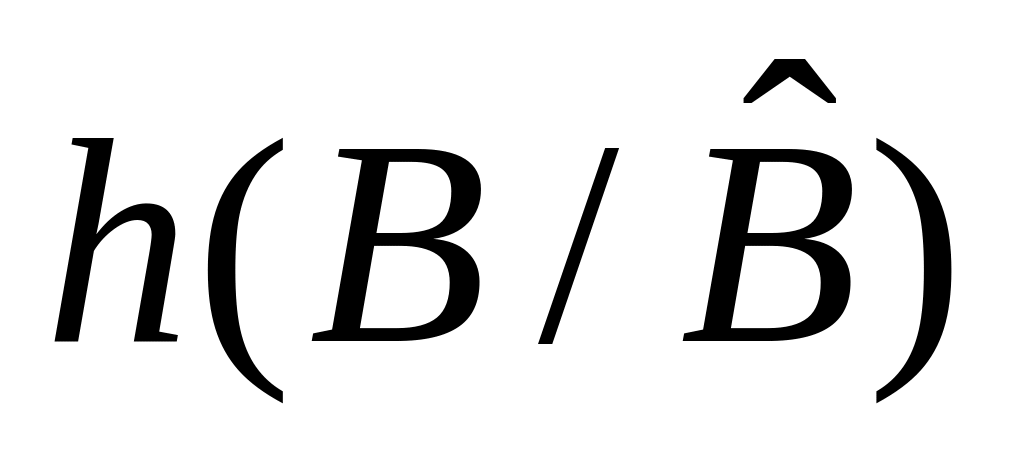• эпсилон-энтропия джерела ;

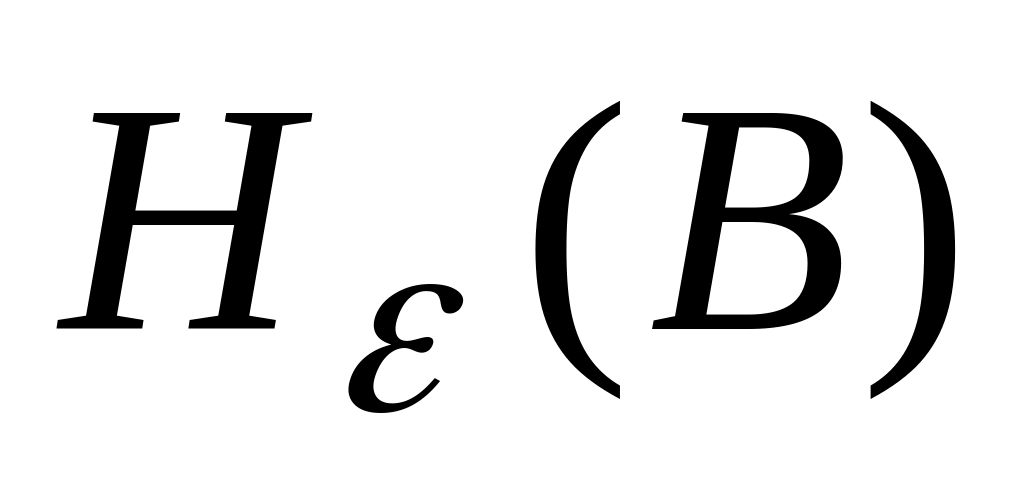• коефіцієнт надмірності джерела ;

• продуктивність джерела ;

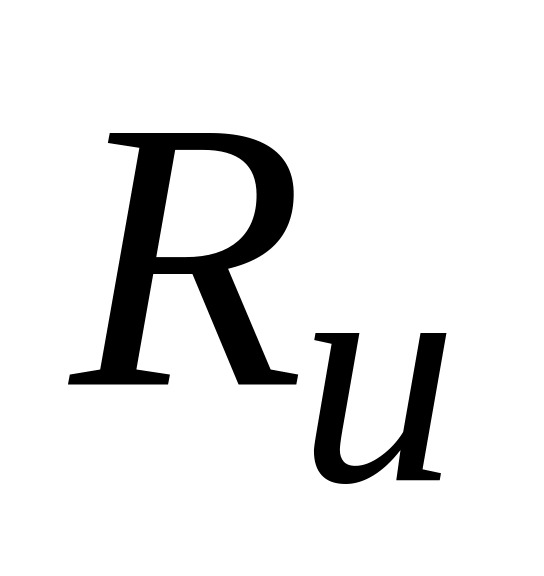• пропускна здатність каналу зв'язку С.

Диференціальна ентропія й умовна ентропія обчислюються виходячи з відомих функцій розподілу щільності ймовірності. Диференціальна ентропія сигналу залежить від виду розподіл імовірностей і дисперсії сигналу , і відповідні розрахункові формули для її обчислень наведені в табл. 1. У сигналів із середнім значенням рівним нулю .

При розрахунках думають, що помилка відтворення на виході системи передачі є гаусовською. При обчисленні умовної ентропії використається значення дисперсії помилки відтворення (потужності перешкоди на виході системи передачі) . Значення визначається по заданому відношенню сигнал/перешкода й середньої потужності сигналу виходячи з формули:

де - середня потужність первинного сигналу;

- середня потужність перешкоди на виході системи передачі.

До обчислень задане в децибелах відношення необхідно представити в разах:

.

Коефіцієнт надмірності джерела обчислюється на основі значення епсілон-энтропіі й максимально можливого значення .

Продуктивність джерела , що називають епсілон-продуктивністю, обчислюють у припущенні, що відліки випливають через інтервал Котельникова.

Вимоги до пропускної здатності безперервного каналу зв'язки формулюються на основі теореми кодування для каналу з перешкодами.

Таблиця 3.1 - Диференціальна ентропія для деяких законів розподілу випадкових величин

Розподіл імовірності	Диференціальна ентропія , біт/відлік
Нормальний розподіл (рис. 3.1а)
Двосторонній експонентний розподіл (рис. 3.1б)
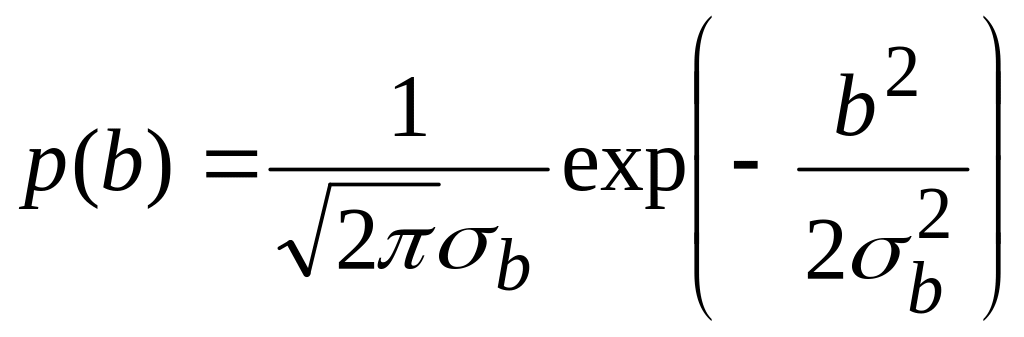
Р івномірний розподіл (рис. 3.1в)