Лекція 4. Нормативний і розрахунковий опір матеріалу. Коефіцієнт надійності за матеріалом

4.1. Криві розподілу випадкових величин

Оскільки механічні характеристики матеріалів і навантаження на конструкції мають випадковий розкид, їх дослідження потребує залучення імовірнісних методів. Тому розгляд поставленого в цьому розділі питання почнемо із викладу деяких положень теорії імовірності і математичної статистики, що стосуються випадкових величин.

4.1.1. Основні визначення. Випадковою величиною (ВВ) називається змінна величина, що у результаті випробування (реалізації) може прийняти те чи інше значення, причому невідомо наперед, яке саме.

Приклади випадкових величин, пов’язаних із будівельними конструкціями:

· геометричні розміри елементів;

· фактичні значення навантажень;

· механічні властивості матеріалів;

· умови експлуатації конструкцій.

Позначення: - випадкова величина; х – її можливе значення.

Імовірністю події А або ВВ називається чисельна міра ступеня об’єктивної можливості цієї події або ВВ, позначення Р(А), Р(х).

Поняття ймовірності тісно пов’язано з поняттям частоти. Якщо у серії з n випробувань подія А трапляється у m випадках, частота визначається як

.

(4.1)

Якщо кількість випробувань необмежено росте, частота асимптотично прямує до ймовірності, згідно з теоремою Бернуллі

, .

(4.2)

Наприклад: кидання монети, коли Р(А) = Р(В) = 0,5, якщо , де А - випадіння “орла”, В - випадіння “решки”.

4.1.2. Криві розподілу ВВ. Для характеристики ймовірності ВВ уводиться функція

.

(4.3)

Ця функція дорівнює ймовірності того, що випадкова величина виявиться меншою від деякого її значення х; ця функція називається інтегральною функцією розподілу випадкової величини, або просто функцією розподілу. У випадку позитивної неперервної ВВ функція розподілу має характер, що ілюструється рис. 4.1.

Рис. 4.1. Інтегральна функція розподілу випадкової величини

Похідна функції F(x)

(4.4)

називається диференційною функцією розподілу або густиною (щільністю) розподілу випадкової величини . Графік функції називається кривою розподілу (рис. 4.2).

Рис. 4.2. Крива розподілу випадкової величини

Важливими є наступні співвідношення:

·	;	(4.5)
·	;	(4.6)

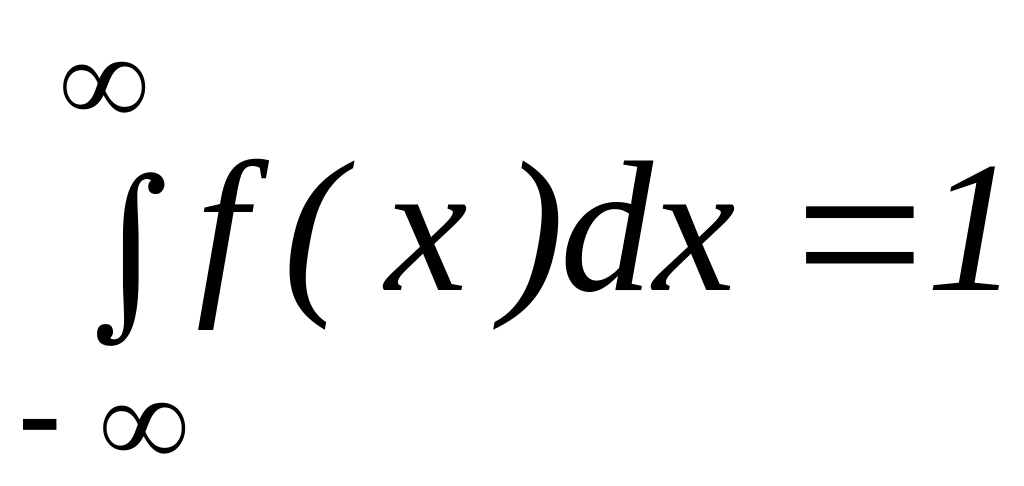· – умова нормування, згідно з якою площа під

кривою розподілу дорівнює одиниці.

4.1.3. Числові характеристики розподілу випадкових величин

Математичне сподівання (очікування):

.

(4.7)

Математичне сподівання визначає положення розподілу, геометрично воно інтерпретується як центр ваги площі, обмеженої кривою розподілу і віссю абсцис (рис. 4.3).

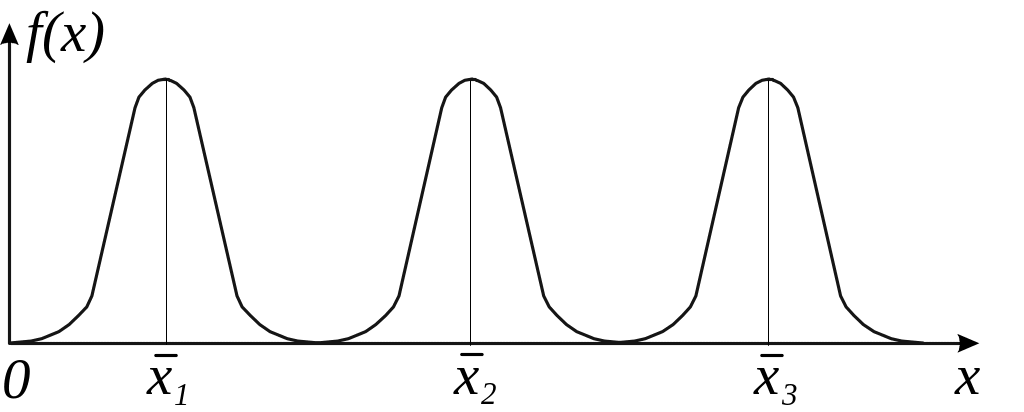
Рис. 4.3. Криві розподілу із різними математичними сподіваннями (EMBED Equation.3 ).

Дисперсія, стандарт, коефіцієнт варіації.

Дисперсія - це математичне сподівання квадрата відхилення ВВ від її центра

.

(4.8)

Геометрично дисперсія може розглядатися як центральний момент інерції площі, обмеженої кривою розподілу.

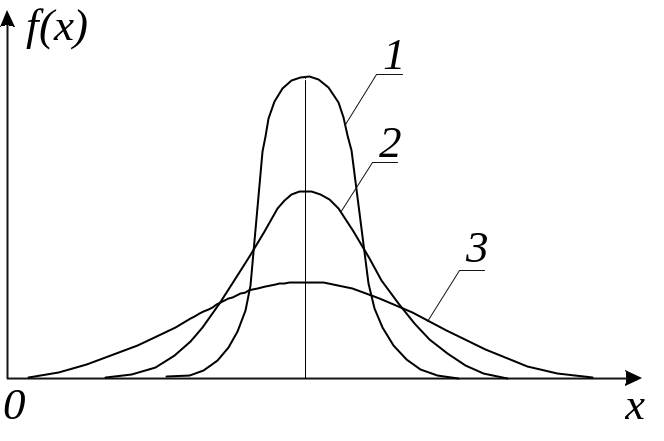
Рис. 4.4. Криві розподілу із різними стандартами ( ).

Середнє квадратичне відхилення (стандарт) і коефіцієнт варіації V характеризують розкид значень випадкової величини (рис. 4.4)

.

(4.9)

Коефіцієнт асиметрії А_х визначає скошеність розподілу випадкової величини (рис. 4.5-а)

,

(4.10)

де - центральний момент третього порядку, він дорівнює

.

Ексцес Е_х оцінює шпилястість (приплюснутість) розподілу випадкової величини (рис. 4.5-б):

.

( 4.11 )

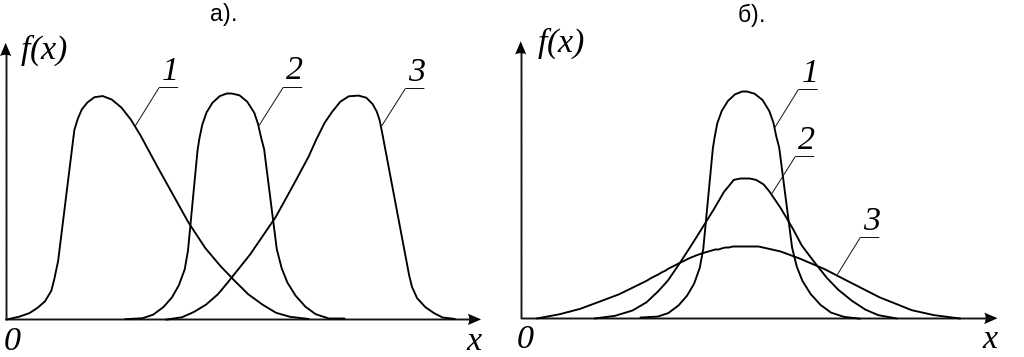Рис. 4.5. Криві розподілу: а) з різною асиметрією ( , , );
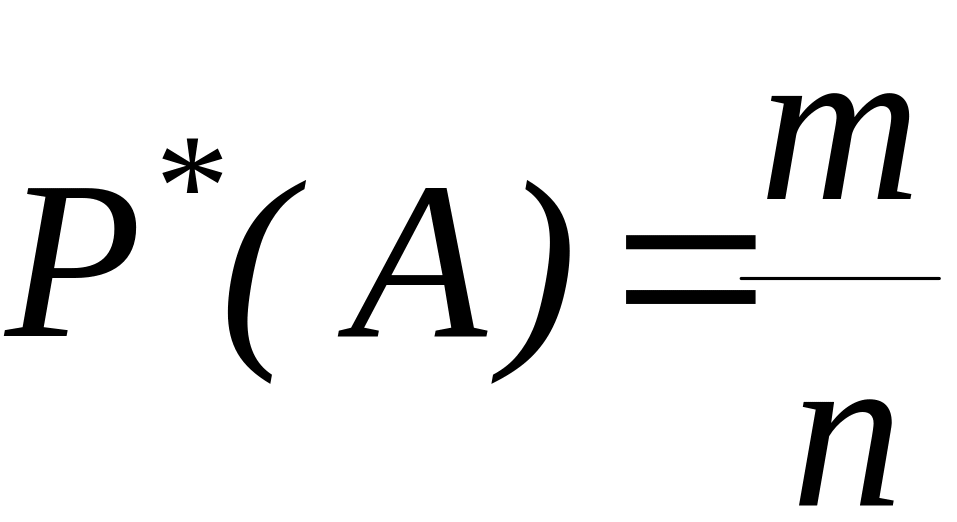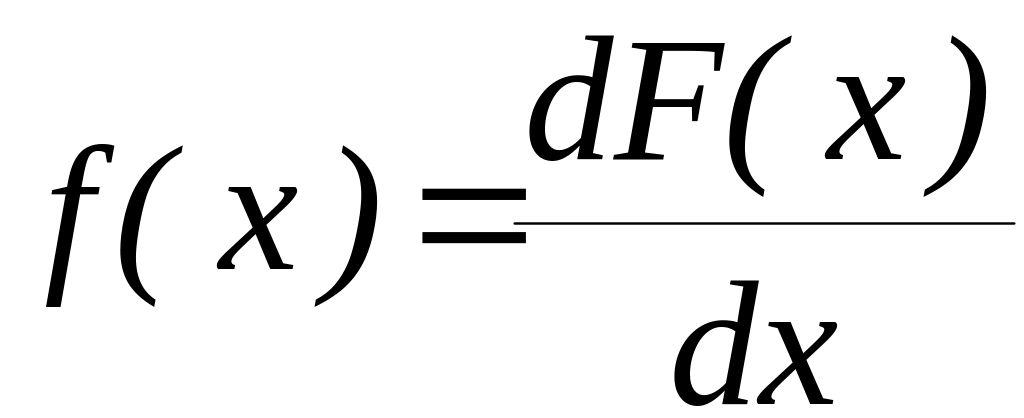
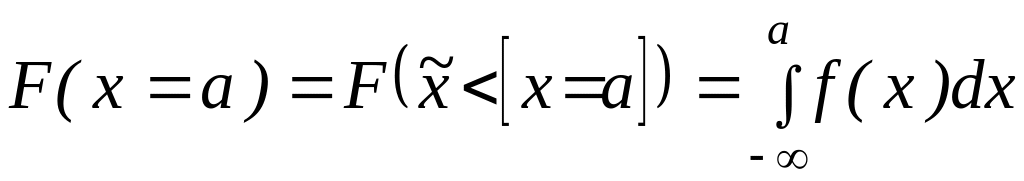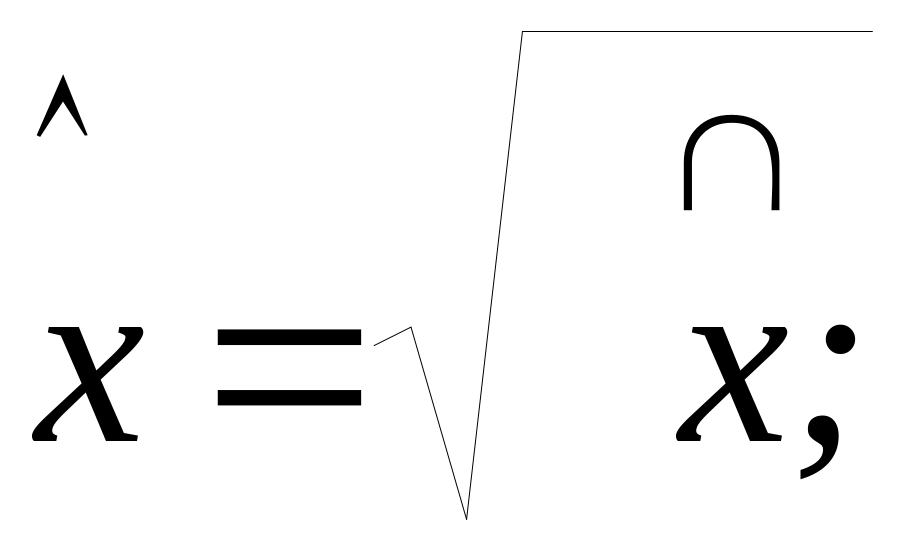
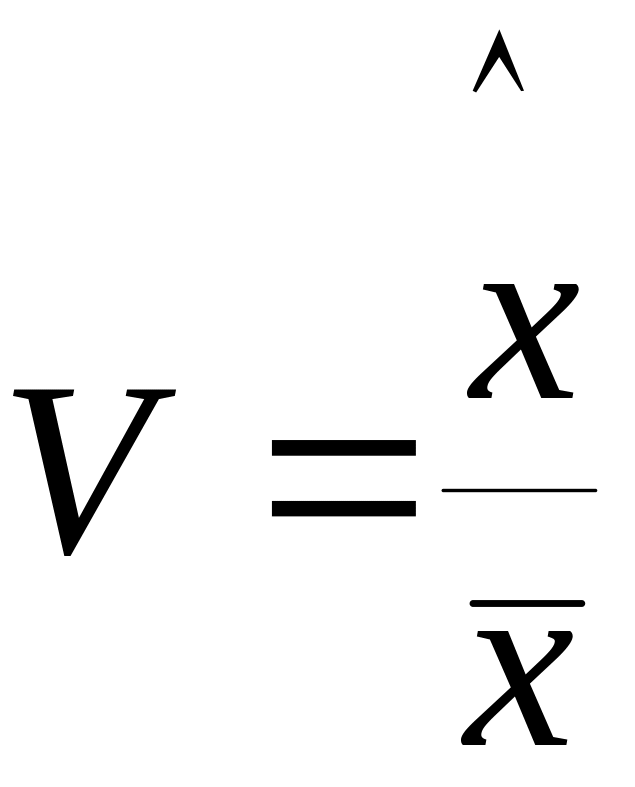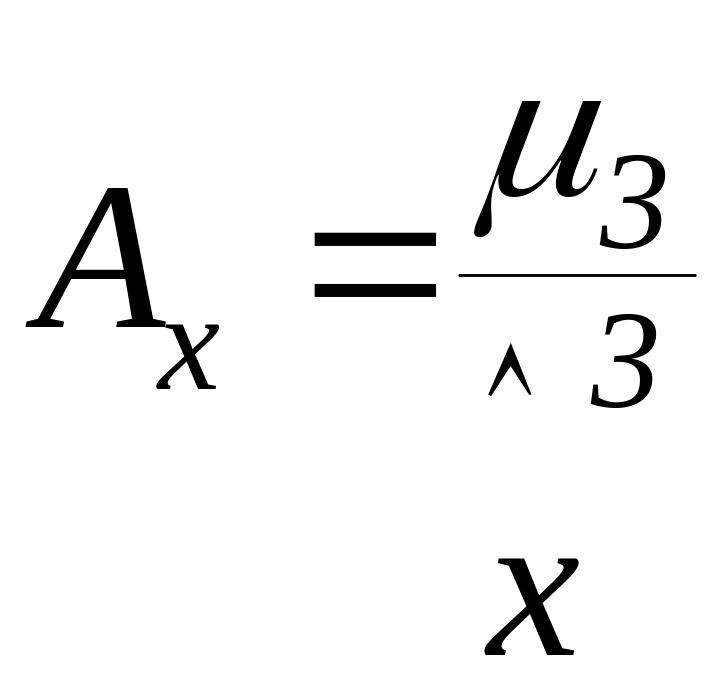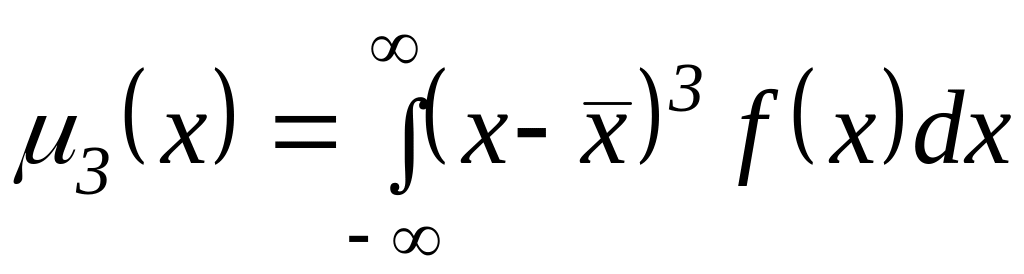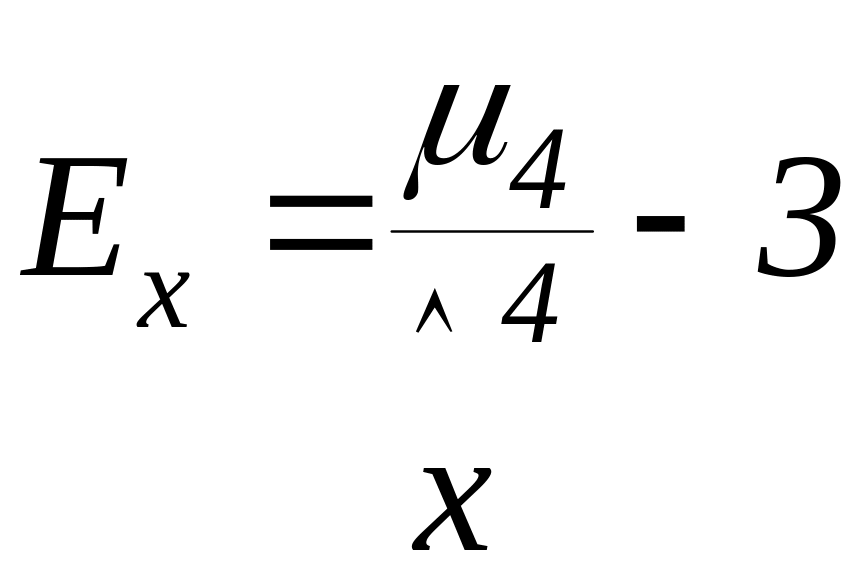