Типичные объекты и их характеристики
Типичными объектами в системах управления являются:
-
Безинерционное звено
-
Звено с чистым запаздыванием
-
Апериодическое звено 1-го порядка
-
“Черный ящик”.
Для каждого из этих объектов весовая функция имеет следующий вид:
|
|
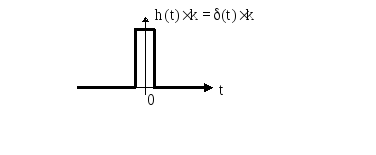
Безинерционное звено с коэффициентом усиления k h(t)=(t) |
|
|
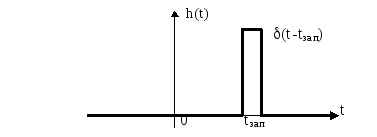
Звено с чистым запаздыванием h(t)=(t-tзап) |
|
|
Апериодическое звено 1-го порядка 1 et/T1 при t0 h(t)= Т1 0 при t<0 |
|
|
“Черный ящик” - задается только своей весовой функцией |
При моделировании объектов требуется задать соответствующие параметры, запрограммировать реакцию объекта (в соответствии с его типом), подать на вход пробное входное воздействие в виде ангалога -функции и увидеть дискретные аналоги приведенных выше весовых функций (как реакцию объекта на такой входной сигнал).
Способы описания случайных сигналов
На практике случайные сигналы представляются своими реализациями. В реализацию входит некоторый набор случайных чисел. Развитие конкретной реализации случайного процесса нельзя заранее предсказать в точности, поэтому приходится иметь дело с вероятностными характеристиками сигнала. Привлечение вероятностных оценок предполагает:
-
наличие некоторого гипотетического множества реализаций и вычисление требуемых характеристик с рассечением всего этого множества в некоторый(ые) момент(ы) времени;
-
определение момента времени, для которого рассчитывается та или иная характеристика с использованием данных, выбираемых из каждой реализации для этого момента времени.
Для стационарных процессов статистические характеристики остаются неизменными (и следовательно, равными между собой) для любого момента времени.
На практике исследователь часто имеет доступ к единственной реализации сигнала, и вынужден производить расчеты статистических оценок, используя усреднение по времени. При этом вводят допущение об эргодичности процесса, когда с увеличением интервала наблюдения (строго говоря, до ) оценки, вычисляемые усреднением по времени для единственной реализации, сходятся к соответствующим статистическим характеристикам множества. Последнее делает правомерным распространение полученных результатов на любые другие отрезки той же реализации и на другие реализации множества.
Для описания свойств случайных сигналов используют плотность распределения вероятности для мгновенных значений сигналов, а также ее моменты:
-
первый начальный момент, или математическое ожидание;
-
второй центральный момент, или дисперсию.
Указанных характеристик достаточно для описания свойств последовательности независимых случайных чисел.
В более общем случае для описания статистических взаимосвязей внутри процесса, развивающегося во времени, используют ковариационную функцию. Ее определяют следующим образом: сначала сигнал центрируют, т.е. вычитают из него среднее значение (математическое ожидание сигнала). Затем, используя множество реализаций, дважды рассекают его: сначала в некоторый момент времени t, и затем - сдвинувшись от этого момента на интервал , т.е. в момент t + . При этом в каждой реализации появляется пара отсчетов, сдвинутых по времени на интервал . Затем вычисляют произведение этих пар в каждой реализации и усредняют их значения по всему множеству. Формально ковариационная функция определяется как среднее (по множеству) произведение двух центрированных значений сигнала, сдвинутых по времени на интервал, равный аргументу ковариационной функции:
Kxx()=M{x(t) x(t+)},
где M{...}- знак математического ожидания, обозначающий процесс интегрирования выражения в фигурных скобках с плотностью вероятности появления случайной величины.
При нулевом значении аргумента ковариационная функция автоматически определяет дисперсию процесса, а вот характер ее убывания по мере роста аргумента характеризует процесс исчезновения устойчивых статистических временных связей между разнесенными во времени парами отсчетов в сигнале.
Для предельного случая, когда отсутствует какая-либо статистическая взаимосвязь между парами отсчетов сигнала, сдвинутых на любой значимый интервал времени, процесс подвержен резким флуктуациям (подобно процессу 1 на рис.1). Автоковариационная функция для такого процесса вырождается в -функцию, а спектральная плотность равномерна во всем диапазоне частот, что дало основание называть такой процесс “белым шумом” - по аналогии с белым цветом, являющимся равномерной смесью всех других цветов.
Если же имеется статистическая взаимосвязь внутри процесса (между сдвинутыми во времени парами отсчетов), процесс становится более плавным (подобно процессу 2 на рис.1), а его автоковариационная функция принимает вид плавно затухающей кривой. Такой сигнал часто называют, в отличие от “белого шума”, “окрашенным” сигналом. Обычно такой сигнал при моделировании получают, пропуская “белый шум” через формирующий фильтр.
Введение ковариационной функции и многомерного закона распределения вероятностей позволяет более полно описать свойства случайного сигнала. Вместе с этим для каждого конкретного момента времени наиболее полной характеристикой амплитудных свойств сигнала является одномерная плотность вероятности, а ее второй центральный момент совпадает со значением ковариационной функции при нулевом аргументе.
Более того, широко распространенный на практике, нормальный или гауссовский закон распределения полностью определяется через свое математическое ожидание и дисперсию. В этом случае ковариационная функция, значение которой при нулевом аргументе совпадает с дисперсией, а характер убывания определяет статистические временные взаимосвязи внутри процесса, начинает играть (вместе с математическим ожиданием) важную роль для полного описания свойств процесса.
Различные динамические преобразования сигнала с любым законом распределения его мгновенных значений, в силу центральной предельной теоремы, ведут к получению результирующего сигнала с гауссовским распределением.
Для оценки амплитудных свойств сигнала вместо плотности вероятности на практике используют гистограммы. Их вид позволяет определить близость к гауссовскому или иному распределению.
Для оценки временных свойств сигнала вместо ковариационной функции используют корреляционную, при расчете которой усреднение ведется не по множеству, а по времени.
![]()
где Т - интервал наблюдения, - аргумент корреляционной функции, изменяющейся от 0 до max. Величину max обычно берут так, чтобы max Т / 10.
При расчетах на ЭВМ используют дискретные аналоги приведенных выше соотношений:
![]()
![]() ,
q=0,1,2, ... , Q
,
q=0,1,2, ... , Q