
Нейронные сети (ИПОВС) / 4 курс - Рычагов М.Н. / Лекции / Lektsiya_1_Neyronnyie_seti_i_mashinnoe_obuchenie
.pdf
Исторический обзор
© 2019 МИЭТ, Нейронные сети |
21 |
|
21 |

Нейрон как структурная единица мозга
Идея нейрона как структурной единицы головного мозга
(Ramon y Cajal, 1911)
Структура биологического моторного нейрона (а) и электронная микрограмма тела нейрона и дендритов (б)
© 2019 МИЭТ, Нейронные сети |
22 |
|
22 |
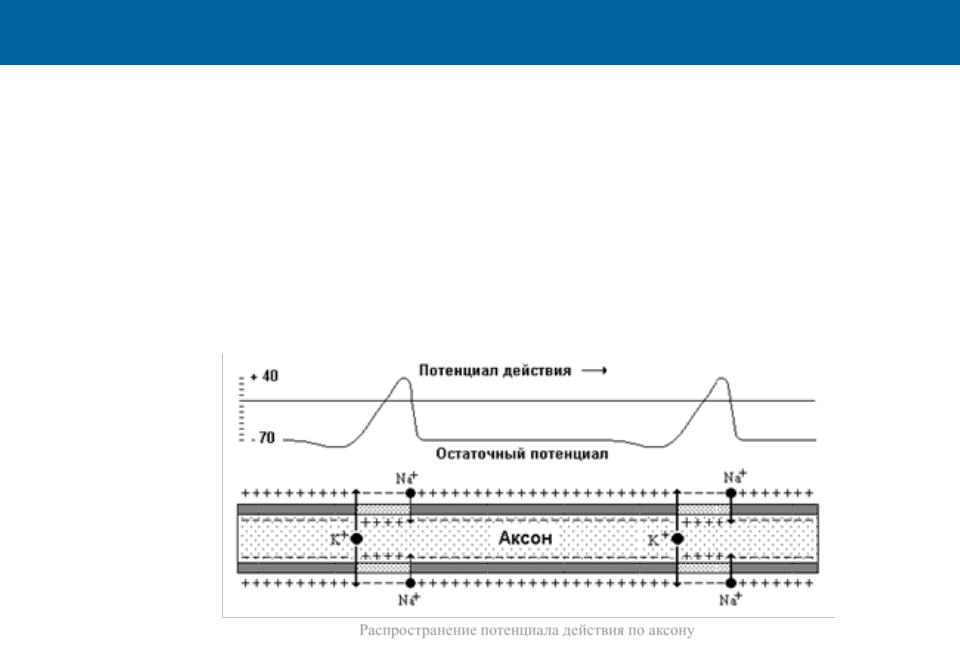
Передачи сигнала в нейроне
Нейрон
▪Имеет тело и отростки - аксоны и дендриты
▪Аксон – длина (~ от сантиметров до 1 м)
▪Длина дендритов обычно не больше 1 мм. Активность в дендритах меняется плавно.
▪Мембранный потенциал клетки от -70 до + (20 - 40) мВ
Распространение потенциала действия по аксону
© 2019 МИЭТ, Нейронные сети |
23 |
|
23 |

Исторический экскурс. 1
1942 Теорема |
Колмогоров , А.Н. 1942 |
аппроксимации |
Mathematical Developments |
многомерной функции 1D |
Arising from Hilbert Problem , |
нелинейных функций |
AMS (1976). |
Каждая непрерывная функция n переменных |
f (x1, x2 ,...., xn ), |
|||
заданная на единичном кубе n-мерного пространства, |
||||
представима в виде |
|
|
|
|
2n+1 |
|
n |
|
|
f (x1, x2 ,...., xn ) = hq |
qp (x p ) |
, |
||
q=1 |
p=1 |
|
||
|
|
|
|
|
где hq ( ) - непрерывна, а qp (x p ) → зависят от выбора функции f.
© 2019 МИЭТ, Нейронные сети |
24 |
|
24 |
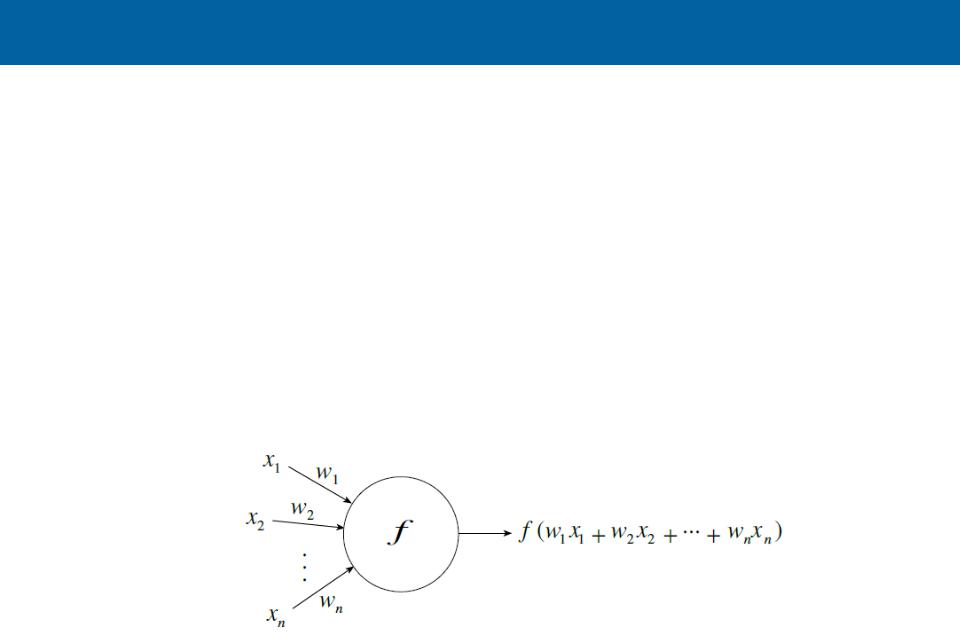
Исторический экскурс. 2
1943 Модель нейрона как |
W.S. McCulloch & W. Pitts |
бинарного элемента с |
Bulletin of Mathematical |
выходным сигналом 0 или 1 |
Biology, 5(4):115–133, 1943. |
(МакКэллок и Питтс ) |
|
1947 Определено |
W.S. McCulloch & W. Pitts |
практическое поле |
Bulletin of Mathematical |
применения – |
Biology, 9(3):127–147, 1947. |
распознавание образов |
|
Абстрактный нейрон
© 2019 МИЭТ, Нейронные сети |
25 |
|
25 |

Распознавание образов
Распознавание рукописных символов/букв/цифр
Биометрия: голос, радужная оболочка, отпечаток пальца, лицо, походка
Распознавание речи
Распознавание запаха (e-нос)
Определение дефектов в производстве интегральных микросхем
Распознавание еды и определение калорий
Медицинская диагностика
Определение террористической опасности (эмоции)
Определение подделки (банковская подпись)
Запрос на кредит
© 2019 МИЭТ, Нейронные сети |
26 |
|
26 |
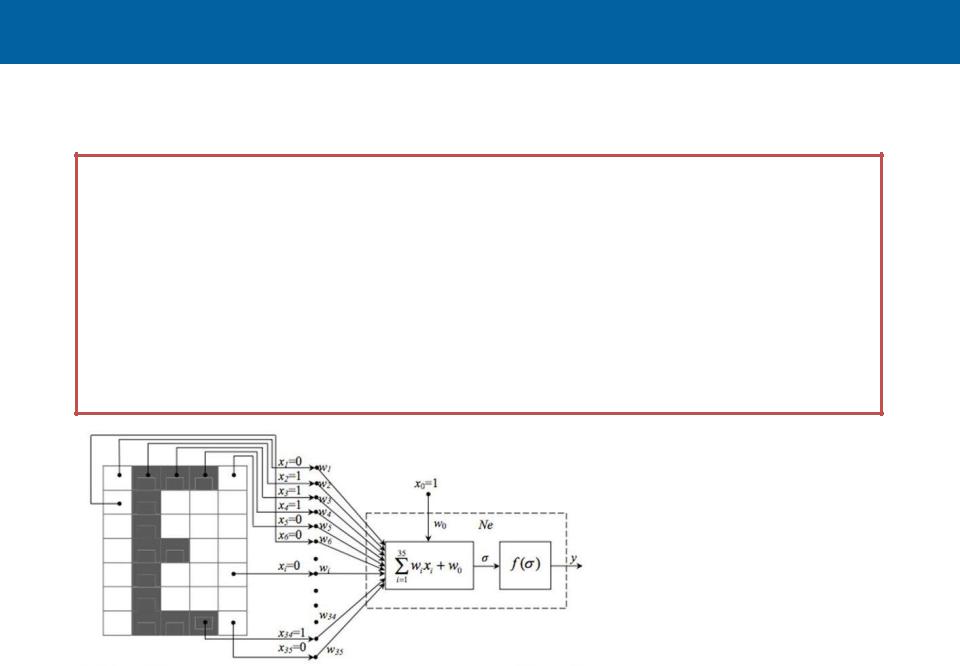
Исторический экскурс. 3
1949 Правила обучения Хэбба (англ. Hebbian rule)
Первое правило Хэбба → Если сигнал перцептрона неверен и равен нулю, то необходимо увеличить веса тех входов, на которые была подана единица.
Второе правило Хебба → Если сигнал перцептрона неверен и равен единице, то необходимо уменьшить веса тех входов, на которые была подана единица.
y = 1, если на входе гласная буква
y=0, если буква - согласная
© 2019 МИЭТ, Нейронные сети |
27 |
|
27 |

Алгоритм обучения Хэбба
© 2019 МИЭТ, Нейронные сети |
28 |
|
28 |

Исторический экскурс. 4
1958-1960 Модель нейрона, доказательство сходимости процесса обучения перцептрона
Первый нейрокомпьютер
Mark I perceptron
Распознавание цифр
Матрица: 20 20 пикселей
512 управляемых моторами потенциометров → изменяющиеся веса
Rosenblatt, F., 1958
Psychological Review, 65, 386408.
Розенблатт (слева) в Cornell Aeronautical Laboratory (1958)
© 2019 МИЭТ, Нейронные сети |
29 |
|
29 |

Исторический экскурс. 5
1969 Математический анализ |
|
Минский М., Пейперт С. |
функциональных |
|
Персептроны.- М.: Мир, |
возможностей простейших |
|
1971. – 261 с. |
нейронных сетей |
|
|
1982 Кохонен Т. Нейронные |
|
|
сети с саморганизацией на |
|
|
основе конкуренции |
|
|
1985 Д. Хопфилд |
Раскраска карты Кохонена |
|
Ассоциативная память |
|
|
1989 Д. Румельхарт, Р. |
|
|
Виллиамс Алгоритм |
|
|
обратного распространения |
|
|
2007 Я. Лекун Сверточные НС |
Обработка данных в СНС |
|
© 2019 МИЭТ, Нейронные сети |
30 |
|
30 |
