
Нейронные сети (ИПОВС) / 4 курс - Рычагов М.Н. / Лекции / Lektsiya_5_Assotsiativnaya_pamyat._Neyronnaya_set_Hopfilda
.pdf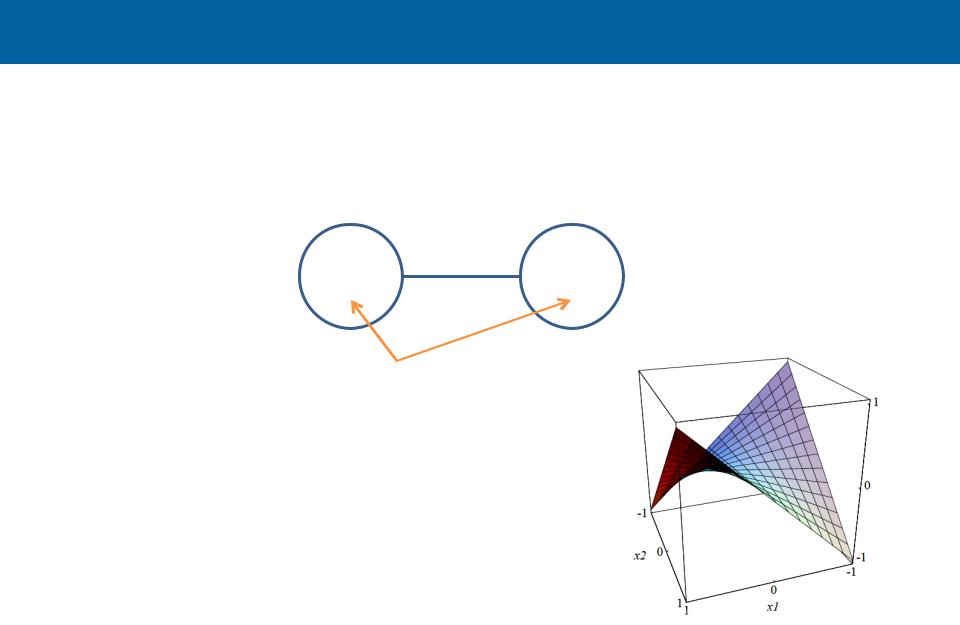
Примеры модели. II
Функция энергии НС Хопфилда –квадратичная форма локальный минимум.
Триггерная ячейка
-1 0 0
Пороговые значения = 0
Единственные устойчивые состояния
(1, -1) и (-1, 1).
Т.к. w12 =w21, будем иметь
E(x1, x2 ) = x1x2
Функция энергии триггерного элемента
© 2019 МИЭТ, |
сети |
21 |
© 2019 МИЭТ, Нейронныесети |
21 |
|

Примеры модели. III-1
Триггер с любым числом устойчивых состояний
Все компоненты вектора = 0, за искл. единственного = 1
Сеть Хопфилда, решающая задачу для n=4
Функционирование:
▪Если сеть запущена со всеми элементами → 0
▪возбуждение каждого элемента тоже будет нулевым, что больше чем порог
▪первый асинхронно выбранный элемент изменит свое состояние до 1.
▪ни один другой элемент не может изменить свое состояние.
© 2019 МИЭТ, |
сети |
22 |
© 2019 МИЭТ, Нейронныесети |
22 |
|

Примеры модели. III-2
Пусть x1, x2, …, xn - двоичные состояния отдельных элементов
Задача: нахождение минимума
|
|
n |
2 . |
|
E(x1, x2 ,..., xn ) = ( xi −1) |
(5.3) |
|||
|
|
i=1 |
|
|
Можно записать в виде |
|
|
|
|
n |
2 |
n |
n |
|
|
+ xi x j − 2 xi +1 |
|
||
E(x1, x2 ,..., xn ) = xi |
(5.4) |
|||
|
|
|
|
|
i=1 |
|
i j |
i=1 |
|
© 2019 МИЭТ, |
сети |
23 |
© 2019 МИЭТ, Нейронныесети |
23 |
|

Примеры модели. III-3
Для бинарных состояний |
x |
= x2 |
, поэтому |
|
|
i |
i |
|
|
|
n |
|
n |
|
E(x1, x2 ,..., xn ) = xi x j |
− xi +1 |
(5.5) |
||
|
i j |
|
i=1 |
|
Что может быть переписано, как
E(x1, x2 ,..., xn ) = − |
1 |
n |
n |
(−1)xi +1 |
|
|
(−2)xi x j + |
(5.6) |
|||
|
2 i j |
i=1 |
|
||
|
|
|
|||
Сравнивая с (5.2) автоматическое решение задачи
|
1 |
n n |
n |
E(x) = − |
|
wij xi x j + i xi . |
|
|
|||
|
2 j=1 i=1 |
i=1 |
|
© 2019 МИЭТ, |
сети |
24 |
© 2019 МИЭТ, Нейронныесети |
24 |
|

Фундаментальная память
•Запоминание образов в памяти → фундаментальная память
•Элементы фундаментальной памяти извлекаются по автоассоциации → по совпадающим или близким последовательностям во входном векторе
|
Реставрация образа |
Дополнение (завершение) образа |
|
|
Источник: Hertz et al., 1991 |
|
|
|
© 2019 МИЭТ, |
сети |
25 |
© 2019 МИЭТ, Нейронныесети |
25 |
|

Близость образов
•Искаженный образ
•Сдвиг, зеркальное отражение, поворот
•Черно-белый, полутоновый ↔ цветной
•Эйджелы (англ. Edgels) ↔ пиксели (англ. Pixels)
•Распознавание в видеопотоке
Выделение краев |
Распознавание в видеопотоке |
© 2019 МИЭТ, |
сети |
26 |
© 2019 МИЭТ, Нейронныесети |
26 |
|

Модель ассоциативной памяти.1
• Рассматривается модель всех нейронных «состояний» - V1 и V2
• В этом пространстве,i - фундаментальная
память
•«Ландшафт» энергии (потенциала E) определен
•Фундаментальная память → в минимумах энергии
•Любой i → «намёк»
© 2019 МИЭТ, |
сети |
27 |
© 2019 МИЭТ, Нейронныесети |
27 |
|
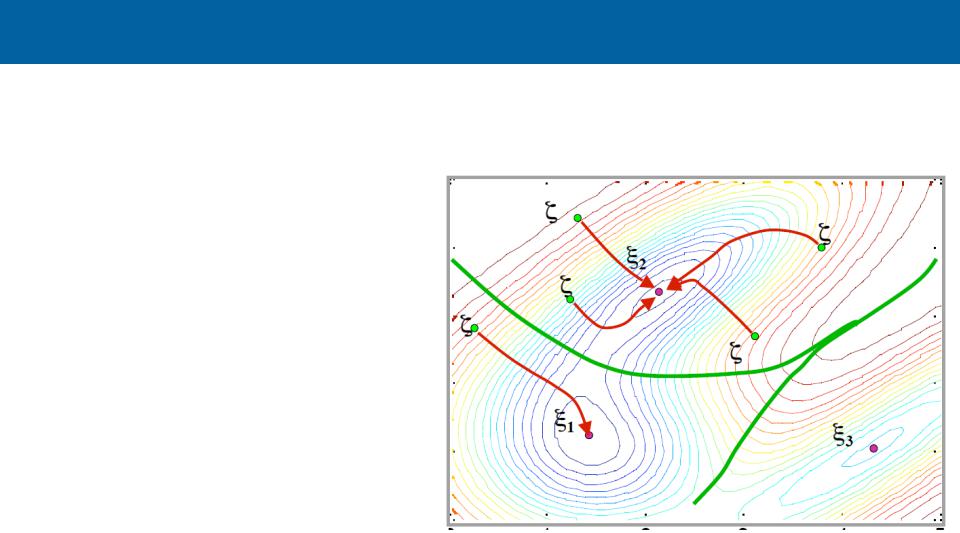
Модель ассоциативной памяти.2
•Аналогично, в контурном представлении
•Пространство образцов образует «бассейны» притяжения
•Фиксированные точки в пространстве сложной структуры аттракторов
© 2019 МИЭТ, |
сети |
28 |
© 2019 МИЭТ, Нейронныесети |
28 |
|

Реальные образцы
© 2019 МИЭТ, |
сети |
29 |
© 2019 МИЭТ, Нейронныесети |
29 |
|
