
Нейронные сети (ИПОВС) / 4 курс - Рычагов М.Н. / Лекции / Lektsiya_5_Assotsiativnaya_pamyat._Neyronnaya_set_Hopfilda
.pdf
Ассоциативная память. Нейронная сеть Хопфилда.
Лекция 5-6
Рычагов М.Н., профессор, д.ф.-м.н.

Однонаправленные и рекурсивные архитектуры
Однонаправленная архитектура – композиция функции
Рекурсивная архитектура – обработка производится в несколько шагов
© 2019 МИЭТ, |
сети |
2 |
© 2019 МИЭТ, Нейронныесети |
2 |
|

Рекуррентные НС
Сложение бинарных чисел – варьируемая размерность входного вектора
Рекурсивная архитектура – перенос (и состояние сети)
сохраняется в процессе арифметического суммирования
1410 +510 = 1910
+ |
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
© 2019 МИЭТ, |
сети |
3 |
© 2019 МИЭТ, Нейронныесети |
3 |
|

Исторический экскурс
1986 Алгоритм обучения однонаправленных нейронных сетей
1982 - 1989 Разработка динамических рекуррентных нейронных сетей
Фото с сайта Принстонского университета
Rumelhart, D.E. et al. 1986 Nature, 323, 533-536.
Hopfield, J.J., 1982 Proceedings of American NAS, 79, 2554-2558.
2009 - IEEE Computational Intelligence Society → Frank Rosenblatt Award за вклад в понимание обработки информации в биологических системах (нейродинамика)
Почетный профессор в Принстонском университете
Член Национальной академии наук США Член Американского физического общества
Медаль Дирака Международного центра теоретической физики
© 2019 МИЭТ, |
сети |
4 |
© 2019 МИЭТ, Нейронныесети |
4 |
|

Ассоциативная память (предпосылки)
Моделью мозга является нейронная сеть
Отдельные нейроны и их функционирование вполне хорошо изучены
Распространенное мнение и понимание: информацияв синаптических связях
Открытый вопрос: каким образом осуществляется запоминание информации (образов)?
А также: извлечение информации (образов)
© 2019 МИЭТ, |
сети |
5 |
© 2019 МИЭТ, Нейронныесети |
5 |
|

Примеры модели. I
Предположение – отдельные узлы нейронной сети
сохраняют свое состояние до следующего выбора в качестве |
|
|
|
|||||||
активного элемента |
Связи – преставление в виде n n |
|||||||||
|
|
|||||||||
|
|
|
матрицы с весовыми коэффициентами |
|||||||
Элемент 1 |
|
|
W = |
wij |
|
|
|
|
|
|
|
|
Диагональные элементы нулевые |
|
|
||||||
|
|
|
Случай недиагональных элементов |
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
Осцилляции |
|
|
|
|
|
|||
|
|
|
−1 0 |
0 |
1 |
|
−1 |
|||
|
|
|
|
0 |
−1 |
|
|
|
|
|
Элемент 2 |
Элемент 3 |
W = |
0 |
1 |
|
−1 |
||||
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
−1 |
1 |
|
−1 |
|||
© 2019 МИЭТ, |
сети |
6 |
© 2019 МИЭТ, Нейронныесети |
6 |
|
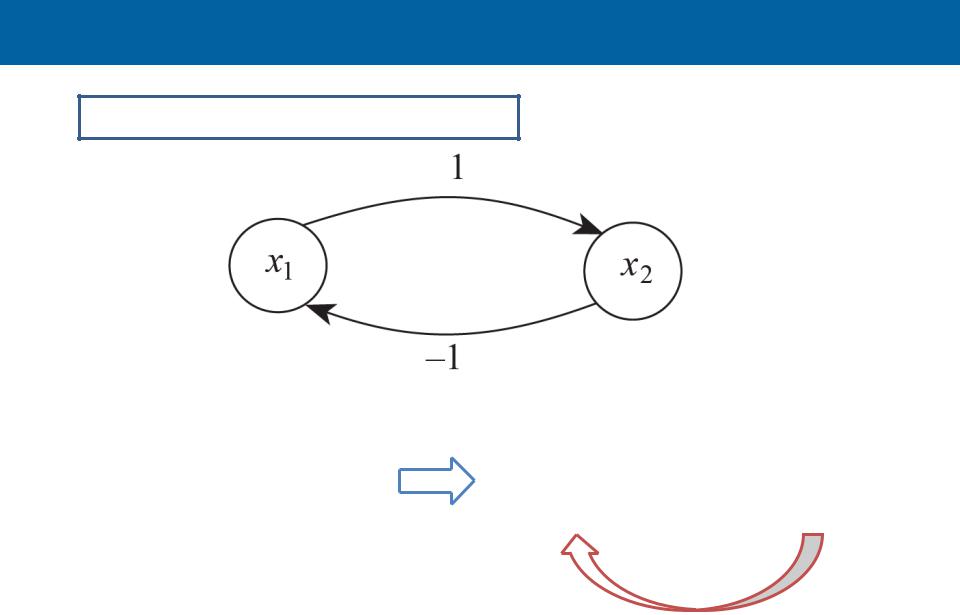
Примеры модели. II
Cлучай асимметричного соединения
0 |
−1 |
|
|
|
|
W = |
|
|
1 |
0 |
|
|
1 |
|
1 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
−1 |
|
−1 |
|
−1 |
Отсутствие сходимости к стабильному состоянию
© 2019 МИЭТ, |
сети |
7 |
© 2019 МИЭТ, Нейронныесети |
7 |
|

Синхронный режим работы НС Хопфилда
Сихронный режим работы –
▪последовательно просматриваются нейроны;
▪их состояния запоминаются отдельно и не меняются до тех пор, пока не будут пройдены все нейроны сети;
▪когда все нейроны просмотрены, их состояния одновременно (то есть синхронно, отсюда и
название) меняются на новыетаким образом, достигается моделирование
параллельной работы последовательным алгоритмом
Замечание: возможно бесконечное чередование двух состояний с разной энергией – т.н. динамический аттрактор
© 2019 МИЭТ, |
сети |
8 |
© 2019 МИЭТ, Нейронныесети |
8 |
|

Динамический аттрактор
Поведение нелинейной системы
x |
= ( y − x) |
|
= x(r − z) − y |
y |
|
|
= xy − bz |
z |
Значения параметров
|
|
|
=10; r = 28; b = 8 / 3; |
|
|
|
=1; y(0) = 0; z(0) = 0 |
|
x(0) |
Аттрактор Лоренца |
|
|
|
|
© 2019 МИЭТ, |
сети |
9 |
© 2019 МИЭТ, Нейронныесети |
9 |
|

Динамический аттрактор
Решение в Мatlab для временного интервала [0, 100] и начальными условиями [1, 1, 1]
clear all clc sigma=10; beta=8/3; rho=28; f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3);
-beta*a(3) + a(1)*a(2)];
%'f' is the set of differential equations
%and 'a' is an array containing values of
%x,y, and z variables
%'t' is the time variable
[t,a] = ode45(f,[0 100],[1 1 1]); %'ode45' uses adaptive Runge-Kutta method
% of 4th and 5th order to solve differential equations
plot3(a(:,1),a(:,2),a(:,3))
%'plot3' is the command to make 3D plot
Аттрактор Лоренца (моделирование в Matlab)
© 2019 МИЭТ, |
сети |
10 |
© 2019 МИЭТ, Нейронныесети |
10 |
|
