25. Критерий максимума апостериорной (после-опытной) вероятности.

x – набор выборок сигнала(результат наблюдений);

s – состояние сигнала;

P – вероятность наступления события;

П – плата за ошибку;

W(x|s_j) – Условный закон распределения (закон распределения вероятности того, что приняли выборку х при состоянии s_j);

В условиях, когда известно априорное (до-опытное) распределение состояний s_j, но нет каких-либо обоснованных соображений относительно величин потерь П_jk может быть использован несколько иной подход к выработке правил выбора решений. Найдем, используя формулу Байеса

апостериорную вероятность состояния s_j, когда наблюдается выборка х = (x₁, ..., х_n):

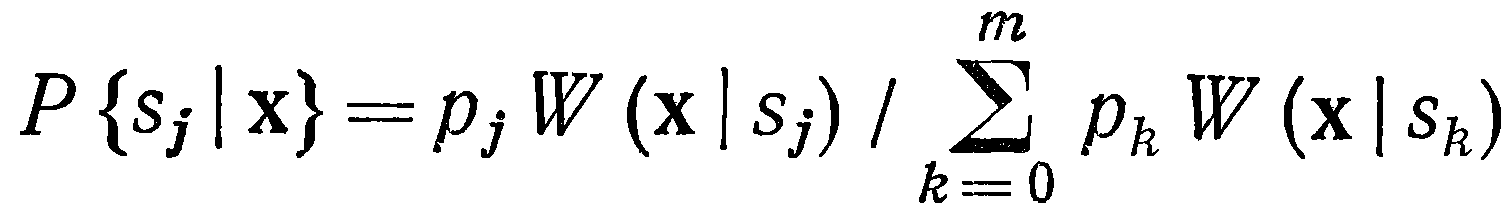(1)

P(s_j | х) — вероятность гипотезы о состоянии s_j при принятии выборки х (апостериорная вероятность);

P_j — априорная вероятность гипотезы о состоянии s_j;

W(х | s_j) — закон распределения вероятности принятия выборки х при истинности гипотезы о состоянии s_j;

—полная вероятность принятия выборки х.

Апостериорные вероятности P{s_j|x}, j= 0, ..., m, представляют наиболее полную характеристику состояний s_j при располагаемых априорных данных. Поэтому естественно принять следующее правило: истинным является то состояние s_j, для которого апостериорная вероятность (1) при наблюдаемом х максимальна. Критерием качества рассматриваемого правила является максимум апостериорной вероятности.

Из этого критерия следует правило разбиения пространства выборок. К области x_j относят те выборки х, для которых при всех

В случае всего двух состояний s₁ и s₀ получаем:

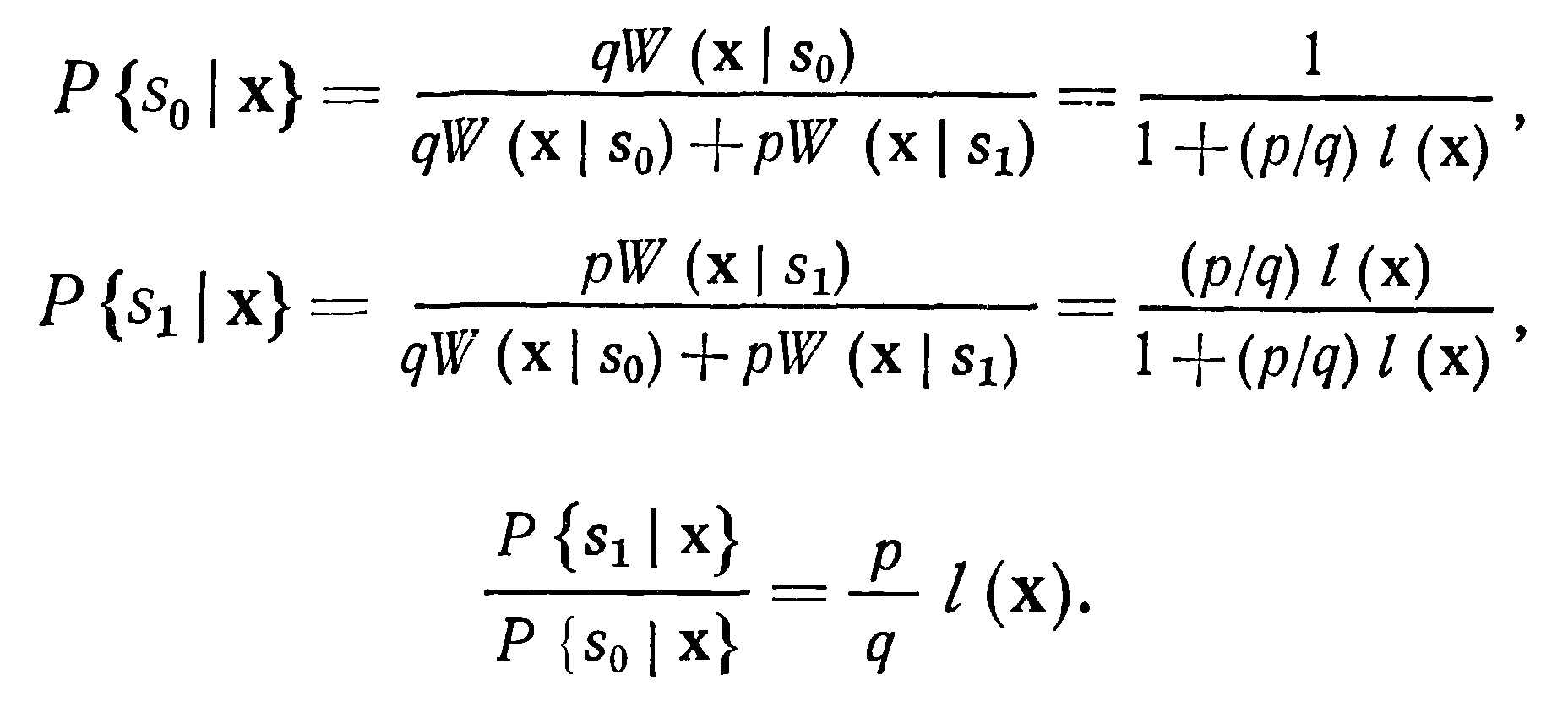(2)

Установим следующее правило выбора решения: принимается гипотеза H1, если P{ s₁ | х } ≥ P{ s₀ | х } (решение γ₁) и отвергается эта гипотеза, если P{ s₀ | х } > P{ s₁ | х } (решение γ₀).

Так как P{ s₀ | х } + P{ s₁ | х } = 1, то это равносильно принятию той гипотезы, для которой апостериорная вероятность больше 1/2 (а при равенстве 1/2 принимается гипотеза H₁).

Используя (2), можно правило выбора решения выразить через отношение правдоподобия: принимается решение γ₁ (отвергается гипотеза H₁), если для наблюдаемой выборки х выполняется неравенство

l(x) ≥ μ (3)

и принимается решение γ₀ (справедлива гипотеза H₀), если выполняется

неравенство, противоположное (3).

Таким образом, максимуму апостериорной вероятности соответствует такая критическая область пространства выборок, точки которой удовлетворяют неравенству (3). Процедура проверки простой гипотезы H₀ сводится в этом случае к вычислению отношения правдоподобия l(x) и сравнению его с величиной μ.

*Теория статистической радиотехники. Левин. Том 2. 1975г. стр.17-18,24-25.

26. Критерий Неймана—Пирсона.

Для оптимизации правила выбора решений при отсутствии априорной информации о потерях и вероятностях состояний применяют критерий Неймана—Пирсона. В ряде случаев оказывается достаточно трудно, а иногда и невозможно определить даже хотя бы приблизительно не только априорные вероятности гипотез, но и цены решений. Классическим примером такой ситуации является обнаружение сигналов в радиолокации. То же самое имеет место и в системах передачи дискретных сообщений при обнаружении начала информационной последовательности (радиограммы, команды и т.п.).

В этих условиях обычно приходится задаваться некоторым значением вероятности ошибочного решения при справедливости одной из гипотез.

Согласно этому критерию выбирается такое правило, которое обеспечивает минимально возможную величину β вероятности ошибок второго рода (пропуск сигнала) при условии, что вероятность ошибки первого рода не больше заданной величины α(ложная тревога). Иначе говоря, правило выбора решения по критерию Неймана—Пирсона имеет наибольшую мощность среди всех других правил, для которых уровень значимости не превосходит α.

Вероятности:

α - ложной тревоги,

β- пропуска сигнала.

Рассмотрим задачу проверки гипотезы Н₀ против альтернативы H₁ в ситуации априорной неопределенности, когда априорные вероятности гипотез, а также матрицы потерь неизвестны. Для указанной бинарной (одноальтернативной) задачи проверки гипотез при использовании любого правила выбора решения возможны два ошибочных решения , и два правильных и . Условные вероятности

называют вероятностями ошибок первого и второго рода соответственно.

Ясно, что вероятности правильных решений

Алгоритм называется оптимальным по критерию Неймана — Пирсона, если при его использовании достигается минимальное значение ошибки второго рода

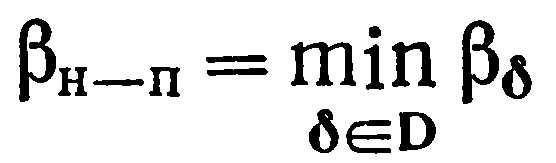
при заданном ограничении вероятности ошибки первого рода .

Задача синтеза оптимального алгоритма принятия решения по указанному критерию состоит в определении минимума функционала

в котором вероятность β зависит от правила выбора решения, вероятность α фиксирована и с — неопределенный множитель Лагранжа.

Для того чтобы применить критерий Неймана-Пирсона на практике необходимо для выборок сигнала х = (х₁, ..., х_n), найти отношение правдоподобия и сравнить с порогом:

причем порог с выбирается из условия

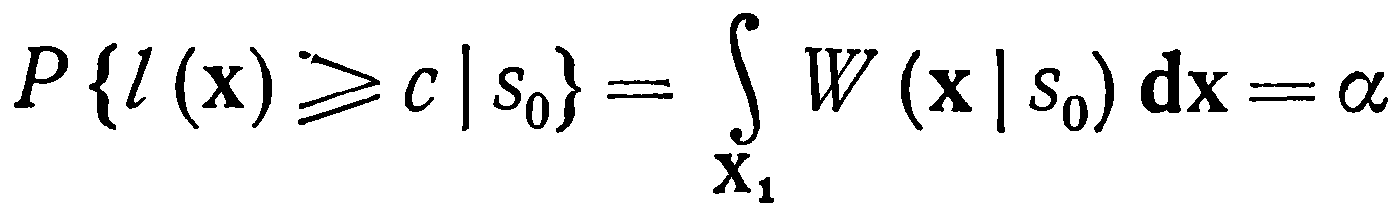
l(x) - отношения правдоподобия ;

c – порог.

s₀ – состояние сигнала;

W(х | s₀) — закон распределения вероятности принятия выборки х при истинности гипотезы о состоянии s_j;

Таким образом, мы задаем значение α и находим порог с.

*Теория статистической радиотехники. Левин. Изд 3е. 1989г. стр.319-320, 330-331.