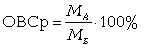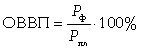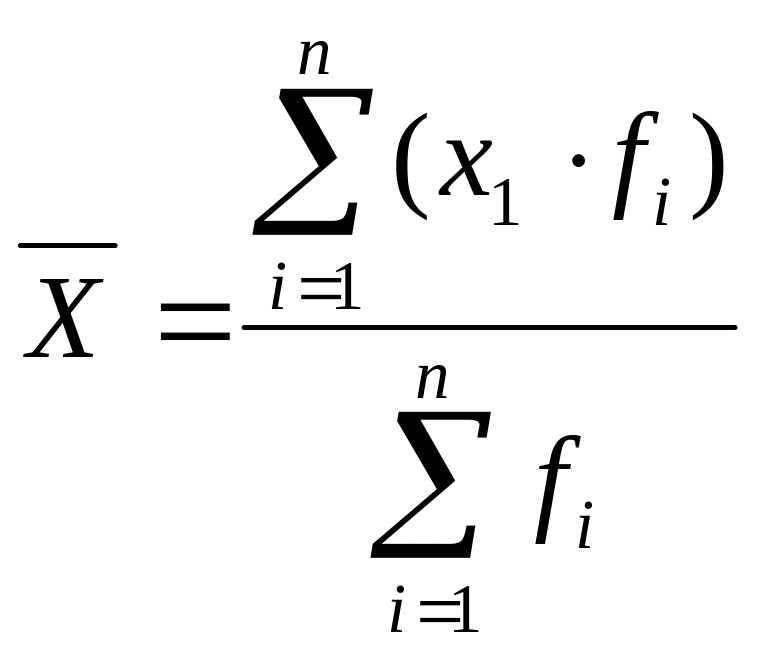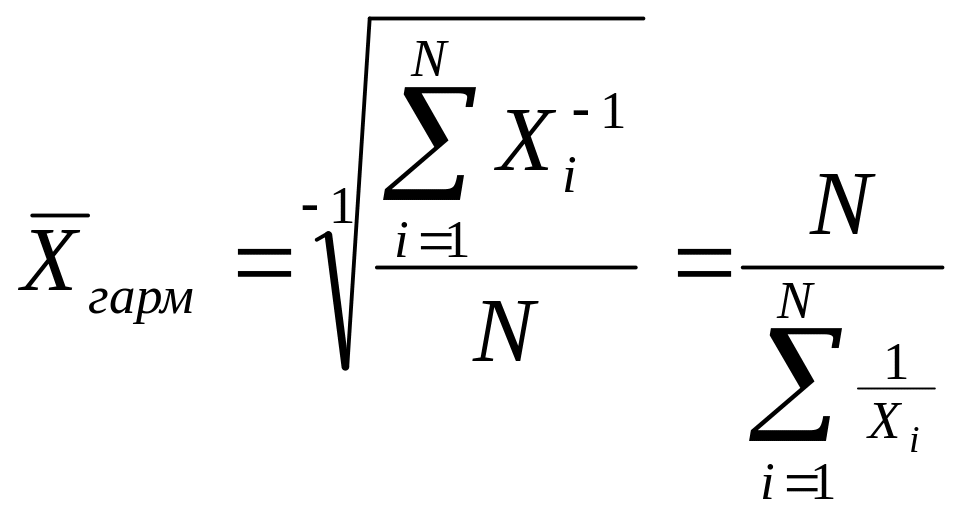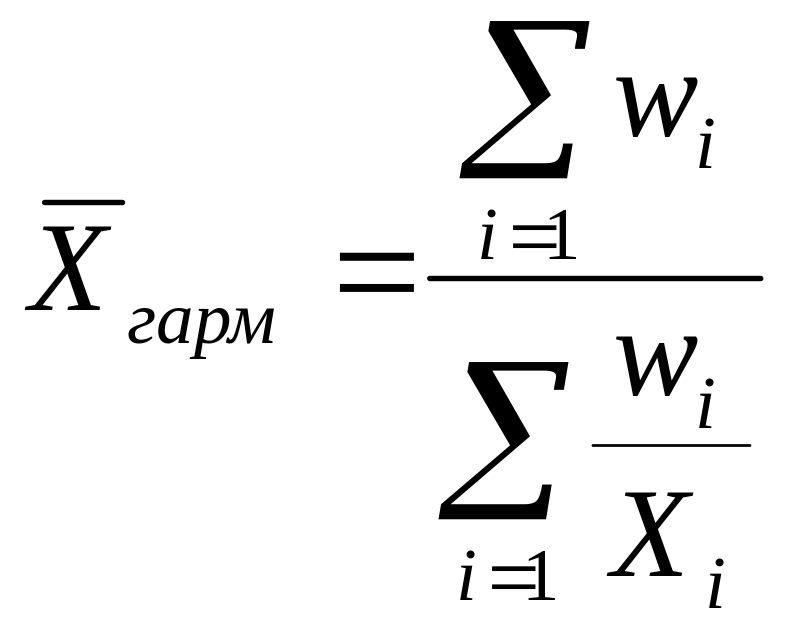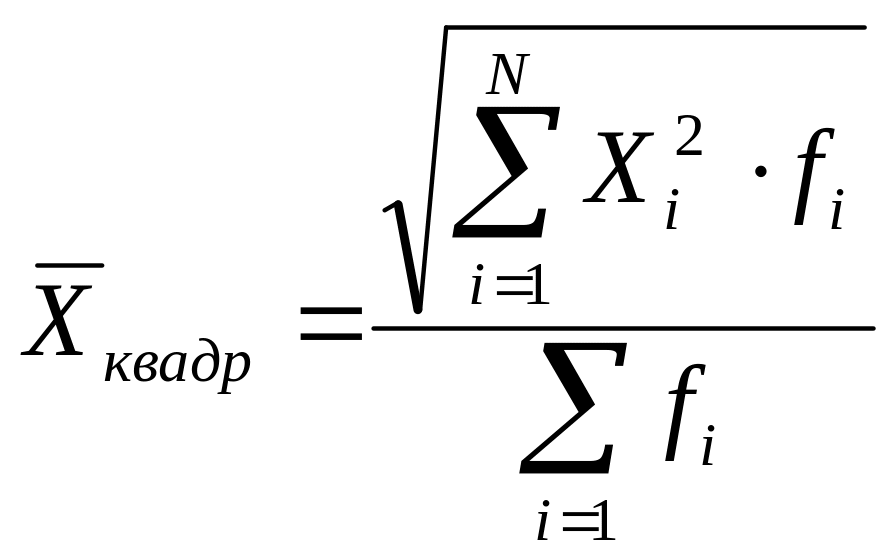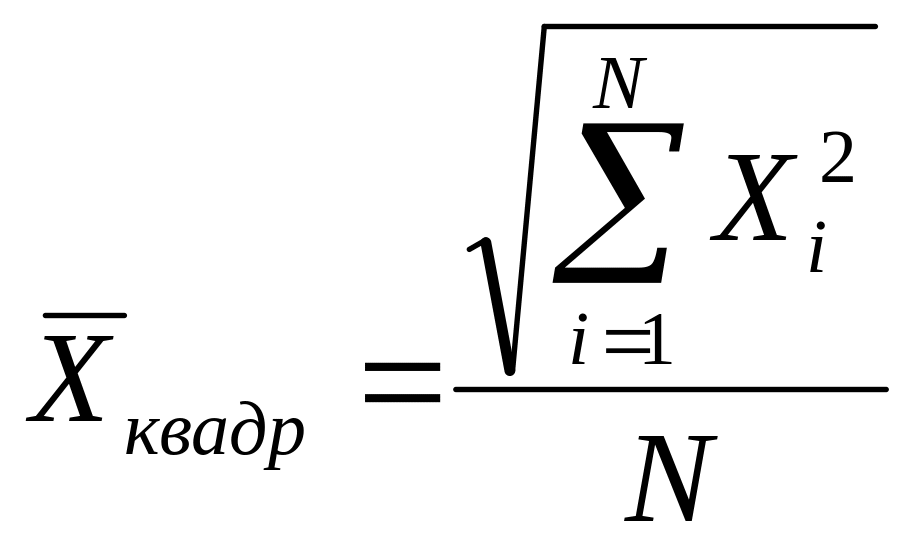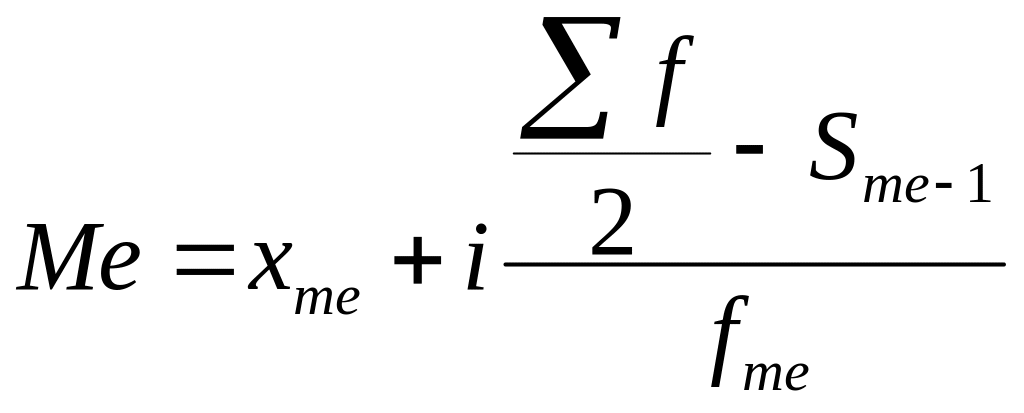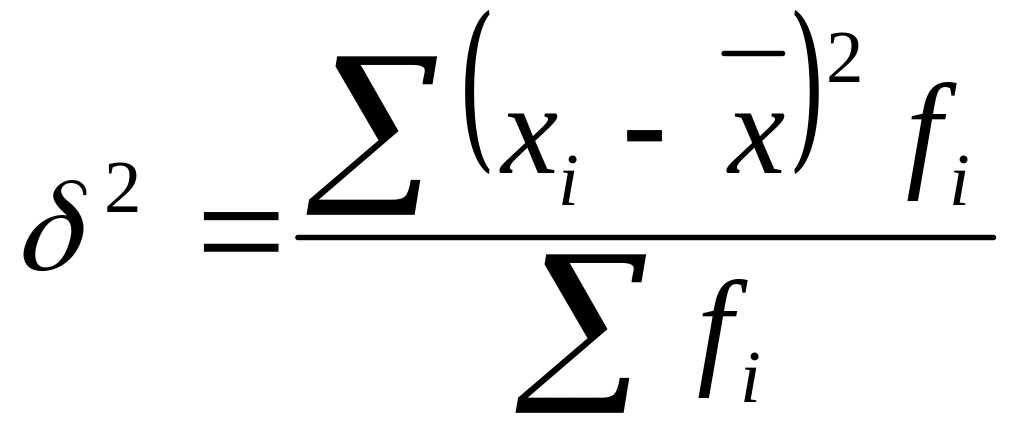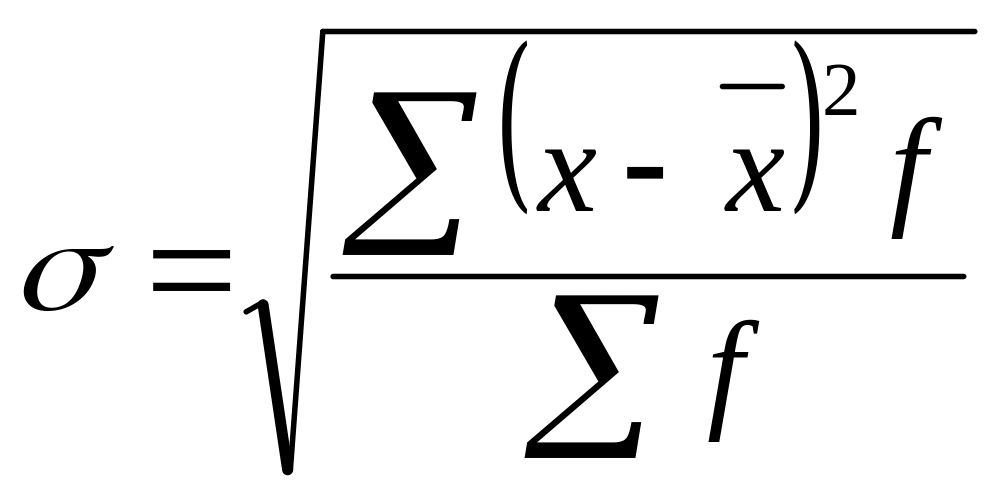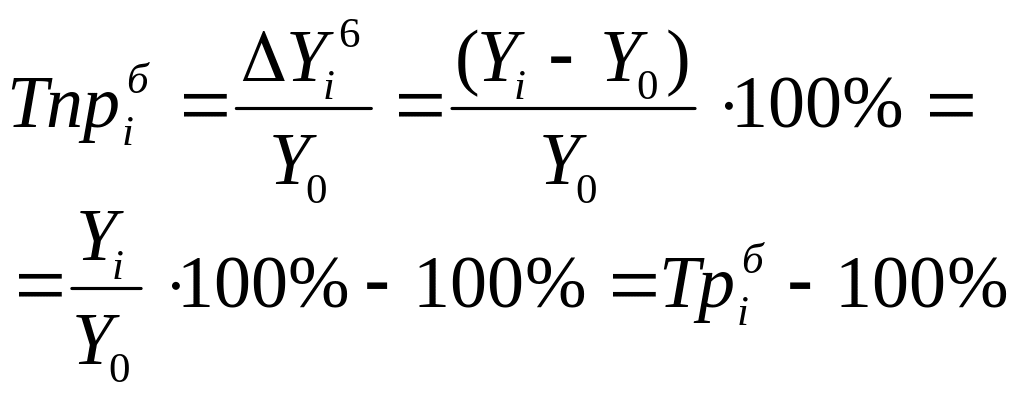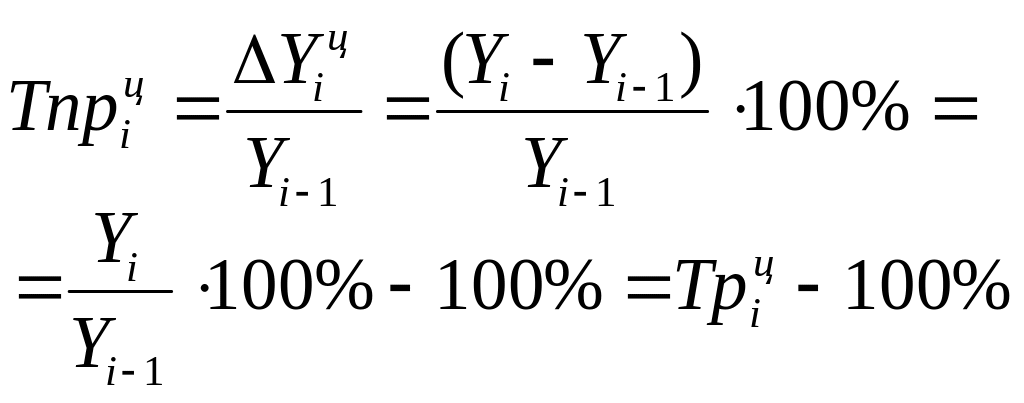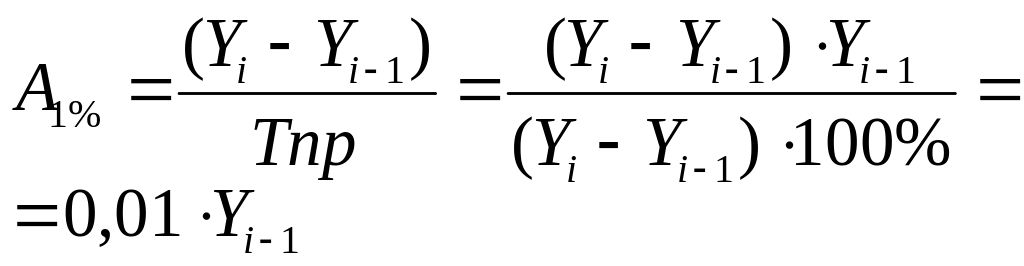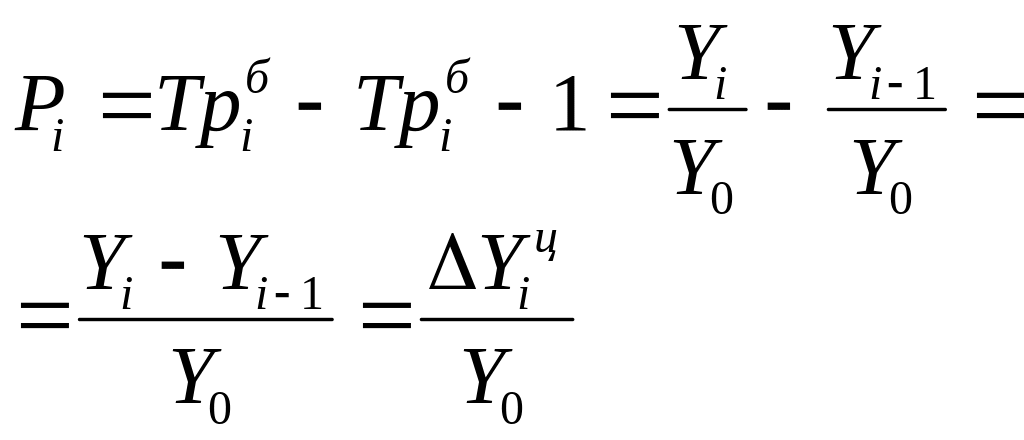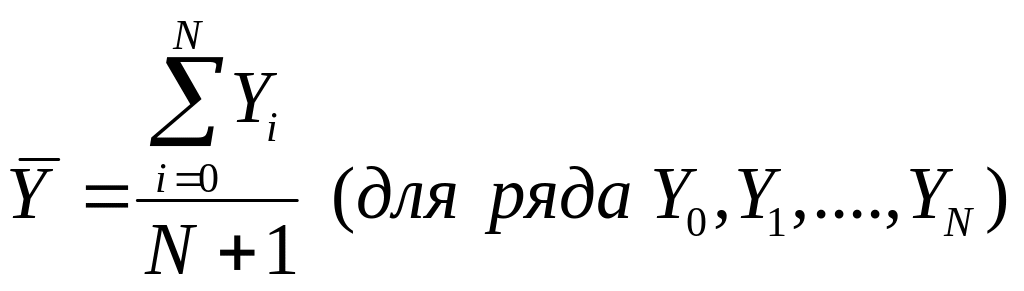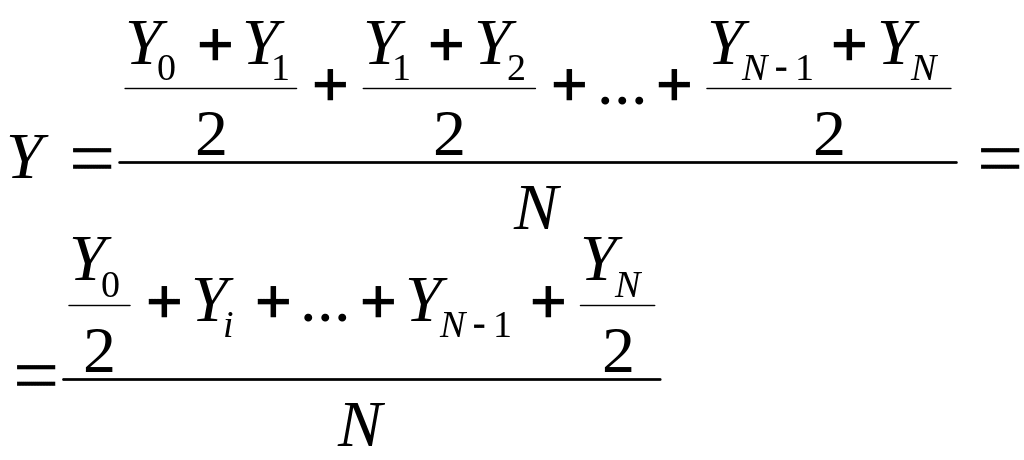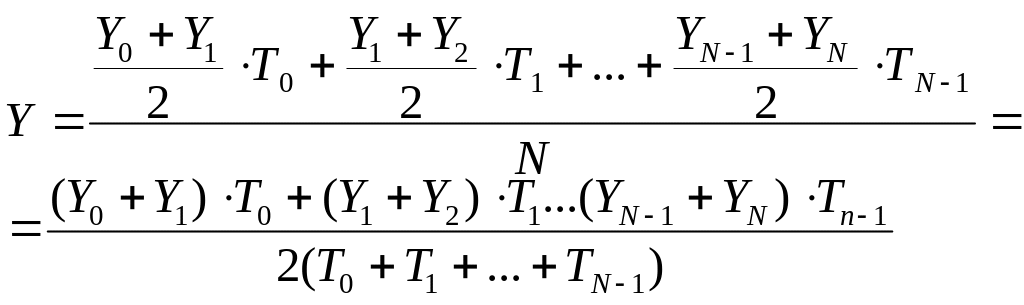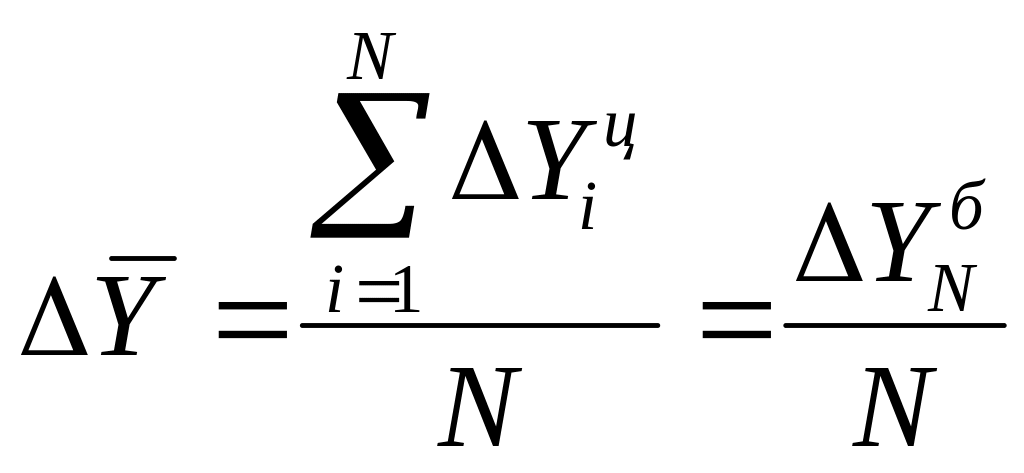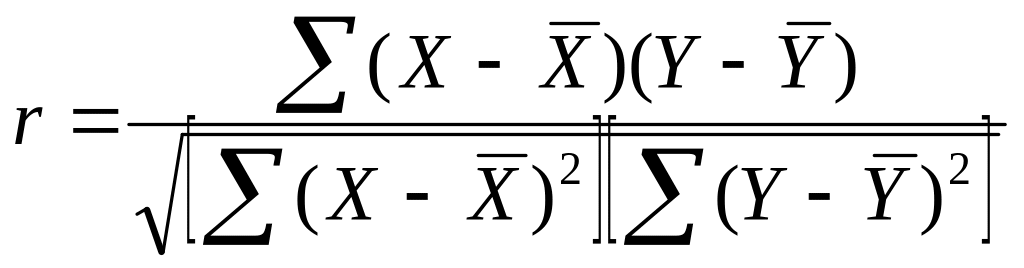Сводка формул

А. Относительные показатели

Отношение

измеряется в долях от единицы

f₁ — количество наблюдений в первой категории;

f₂ — количество наблюдений во второй категории

Удельный вес

измеряется в двух вариантах: либо как отношение, либо в процентах

х – часть целого (предмета, массива, явления)

а – целое (предмет, массив элементов в целом)

Относительная величина структуры (ОВС)

где m_i - объем исследуемой части совокупности;

M - общий объем исследуемой совокупности.

Коэффициент раскрываемости

К_Р = РП / ЗП

где, РП количество раскрытых преступлений;

ЗП число зарегистрированных преступлений в изучаемом периоде

Относительная величина сравнения (сопоставления) (ОВСр)

где М_А - показатель первого одноименного исследуемого объекта;

М_Б - показатель второго одноименного исследуемого объекта (база сравнения)

Коэффициент преступной активности (коэффициент криминальности или коэффициент пораженности)

Коэффициент распространенности преступности по территориям

– это отношение количества зарегистрированных преступлений к площади территории, где данные правонарушения были зарегистрированы.

Коэффициент распространенности преступности по времени

– это отношение количества зарегистрированных преступлений к длительности временного интервала, в котором правонарушения были выявлены и поставлены на учет.

Относительные величины динамики (ОВД)

Относительная величина координации (ОВК)

где m_i - одна из частей исследуемой совокупности;

m_б - часть совокупности, которая является базой сравнения

Коэффициент судимости

– отношение числа осужденных к выявленным лицам

Коэффициент тяжких преступлений

– отношение числа тяжких и зарегистрированных преступлений

Коэффициент интенсивности

Коэффициент преступности (КП)

где П – абсолютно число учтенных (зарегистрированных) преступлений; Н – абсолютная численность населения (в возрасте от 14 лет и старше в целом или отдельных социально-демографических групп)

Коэффициент смертности

– отношение числа погибших людей к числу зарегистрированных преступлений (среднее число лиц, погибших в результате одного преступления)

Коэффициент материального ущерба

– отношение суммы причиненного материального ущерба (млн.руб.) к числу зарегистрированных преступлений (средний материальный ущерб одного преступления)

Относительная величина планового задания (ОВПЗ)

где Р_пл - плановый показатель; Р₀ - фактический (базовый) показатель в предшествующем периоде

Относительная величина выполнения плана (ОВВП)

где Р_ф - величина выполнения плана за отчетный период;

Р_пл - величина плана за отчетный период

Б. Меры центральной тенденции

Средняя

логическая формула

Средняя арифметическая

простая

— среднее арифметическое;

Х – изменяющаяся величина признака;

– сумма значений;

N – количество значений

(число вариантов)

Средняя арифметическая

взвешенная

f_i – вес каждого значения данных x_i

– сумма весов

Средняя гармоническая простая

N – количество значений

(число вариантов);

Х – изменяющаяся величина признака;

∑ – сумма;

Средняя гармоническая взвешенная

w – объемное значение признака: w=xf

Средняя геометрическая простая

N – число вариантов

П – знак перемножения

f_i – вес каждого значения данных x_i

Средняя геометрическая взвешенная

Средняя квадратическая простая

Средняя квадратическая

взвешенная

Мода

В дискретном ряду мода определяется как самое большое число

В интервальном ряду с равными интервалами мода определяется по формуле:

Х_mo – нижняя граница модального интервала

i – величина модального интервала

F_mo – частота модального интервала

F_mo-1 – частота интервала, предшествующая модальному

F_mo+1 – частота интервала, следующая за модальным

В интервальном ряду с неравными интервалами мода определяется по формуле в два шага:

1) относительная частота (частость):

2) относительная плотность:

i – интервалы группировки

∆i – интервальная разность

f _i – частота

φ_i –относительная частота (частость)

Медиана

В интервальном ряду медиана определяется по формуле:

x_me – нижняя граница медианного интервала

i – величина медианного интервала

∑f /2 – полусумма частот

S_{me-1 –} сумма накопленных частот до медианной частоты

f_{me –} частота медианного интервала

В. Меры разброса

Отклонение:

отклонения вариантов признака от его среднего значения

Размах вариации

R=X max - X min

разность между максимальным и минимальным значениями признака

Межквартильный размах:

Q = Q₃ – Q₁

расстояние между верхним и нижним квартилями

Нижний квартиль

Верхний квартиль

Q₁ = ¼(n+1)

Q₃ = ¾(n+1)

Нижний квартиль

Верхний квартиль

Среднее линейное отклонение (невзвешенное):

отклонения вариантов признака от его среднего значения, рассчитанные по модулю (т.е. без учета знаков «+» и «-»)

Взвешенное среднее линейное отклонение:

Дисперсия невзвешенная:

отклонения вариантов признака от его среднего значения, рассчитанные как средний квадрат отклонений

Дисперсия взвешенная:

Стандартное отклонение:

квадратный корень из частного от деления суммы квадратов всех вариант на число единиц совокупности

или

стандартное отклонение есть корень из дисперсии

Стандартное отклонение:

(формула, удобная для расчетов)

Стандартное отклонение взвешенное:

Коэффициент вариации:

процентное отношение среднего квадратического отклонения к средней арифметической

Линейный коэффициент вариации:

или

процентное отношение среднего линейного отклонений к средней арифметической

или

медиане

Коэффициент осцилляции:

процентное отношение размаха вариации к средней арифметической

Г. Показатели динамики

Абсолютный прирост

y = y_i – y₁

представляет собой разность между дву­мя исходными уровнями, один из которых рассматривается как отчетная, оцениваемая величина, а другой принят за базу сравне­ния.

Абсолютный прирост

а) цепной

б) базисный

а) А₁ = у₁ - у_0;

А₂ = у₂ – у₁... А_n = у_n - у_n-1

б) А₁ = у₁ - у_0;

А₂ = у₂ – у₀... А_n = у_n - у₀

а) когда за базу сравнения берут каждый предыдущий уровень;

б) если для срав­нения в качестве базы берется один исходный уровень у₀

Коэффициент роста

(темп роста)

K = y_i / y₁

выражает отношения между собой двух уровней ряда — отчетного и базисного

Коэффициент роста

а) цепной

б) базисный

а) б)

Темп (процент)

прироста

отношение цепного абсолютно­го прироста А_i к предыдущему уровню у_i-1 , %

или отношение (обычно процентное) абсолютного прироста к уровню, взятому для сравнения

Абсолютное значение одного процента прироста

отношение абсолютного прироста к темпу прироста

Пункты роста

разность базисных темпов роста (прироста) смежных периодов

Темп наращивания

деление цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения

Д. Средние характеристики ряда динамики

Средний уровень интервального ряда

по формуле простого среднего арифметического

Средний уровень

моментного ряда

(с равностоящими уровнями)

по формуле среднего хронологического, где (Y₀+Y₁)/2 – средний уровень за период между моментами t₀ и t₁;

(Y₁+Y₂)/2 – средний уровень за период между моментами t₁ и t₂ и т.д.

Средний уровень

моментного ряда

(с неравностоящими уровнями)

по формуле среднего хронологического взвешенного

Т_i – вес равный продолжительности промежутков времени между моментами i и (i+1)

Средний

абсолютный прирост

по формуле простой средней арифметической из показателей абсолютных цепных приростов

Средний относительный прирост

по формуле среднего геометрического из показателей цепных коэффициентов роста

Средний

темп роста

представляет средний относительный прирост (коэффициент роста), выраженный в процентах

Средний

темп прироста

рассчитывается на основе среднего темпа роста, вычитанием из последнего 100%

Е. Меры взаимосвязи

Метод параллельных рядов Фехнера

∑С – число совпадений знаков

∑Н – число несовпадений знаков

∑С+∑Н – общее число наблюдаемых единиц

Коэффициент ассоциации

определяют тесноту связи двух качественных признаков, каждый из которых состоит только из двух групп

Коэффициент контингенции

Коэффициент ранговой корреляции Спирмэна

d – разность рангов х и у

n – число наблюдений пар значений х и у

Коэффициент ранговой корреляции Кендалла

n – число наблюдений

S – сумма разностей между числом последовательностей и числом инверсий по втором признаку

Уравнение регрессии

У – значение зависимой переменной

а – свободный член

b – коэффициент наклона (выражает наклон линии регрессии, или изменение У при единичном изменении Х

коэффициент наклона – b

коэффициент наклона – b

(производна формула удобная в расчетах)

∑ХУ – сумма перекрестных произведений значений

свободный член – а

Коэффициент взаимной сопряженности Пирсона

иное название:

• коэффициент корреляции

• стандартизированный коэффициент регрессии

Связь между переменными, измеряемыми по интервальной шкале

Коэффициент фи