
- •Кафедра гуманитарных и естественнонаучных дисциплин а.Б. Дюбуа, с.Н. Машнина математиЧеский анализ: интегральное исчисление функции одной переменной
- •Рязань 2011
- •Часть 1. Неопределенный интеграл
- •1. Простейшие приёмы интегрирования
- •2. Основные приёмы интегрирования
- •2. 1. Замена переменных в неопределенном интеграле
- •2. 2. Интегрирование по частям
- •2.3. Интегрирование простых дробей
- •2.4. Интегрирование рациональных функций
- •2.5. Интегрирование иррациональных функций
- •2.6. Интегрирование тригонометрических выражений
- •2.7. Интегрирование выражений, содержащих гиперболические функции
- •Задания для самостоятельного решения
- •1. Простейшие приёмы интегрирования
- •2. Основные приёмы интегрирования
- •Ответы:
- •1. Простейшие приёмы интегрирования
- •2. Основные приёмы интегрирования
2.6. Интегрирование тригонометрических выражений
Интегралы вида
![]()
могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки
![]()
При этом функции подынтегрального выражения выражаются через новые переменные
![]() ;
;
 ;
;
![]()
Если при этом
подынтегральная функция
![]() удовлетворяет соотношению
удовлетворяет соотношению
![]()
то выгодно применить
подстановку
![]() .
Например, с помощью этой подстановки
интеграл
.
Например, с помощью этой подстановки
интеграл
![]()
где
— нечетное число, а
![]() — четное, с соответствующей заменой
— четное, с соответствующей заменой
![]()
приводится к интегралу от рациональной функции.
Если эта функция удовлетворяет соотношению
![]()
то выгодно применить
подстановку
![]() .
Например, с помощью этой подстановки
интеграл
.
Например, с помощью этой подстановки
интеграл
где — четное число, а — нечетное, с соответствующей заменой
![]()
приводится к интегралу от рациональной функции.
Если эта функция удовлетворяет соотношению
![]()
то выгодно применить
подстановку
![]() .
Например, с помощью этой подстановки
интеграл
.
Например, с помощью этой подстановки
интеграл
![]()
где
![]() — четные числа, с соответствующей
заменой
— четные числа, с соответствующей
заменой
 ;
;
![]() ;
;![]()
![]()
приводится к интегралу от рациональной функции.
Примеры:
2.6.1.
Найти интеграл:
![]() .
.
■ Подынтегральная
функция является нечётной относительно
синуса и косинуса. Применим подстановку:
![]() ,
тогда
,
тогда
 .
.
Первоначальный интеграл примет вид:

 .◄
.◄
2.6.2.
Найти интеграл: .
.
■ Подынтегральная
функция нечётная относительно косинуса.
Интеграл рационализируется с помощью
подстановки:
![]() .
.
Тогда первоначальный интеграл примет вид:

 .◄
.◄
2.6.3.
Найти интеграл: .
.
■ Подынтегральная функция нечётная относительно синуса. Рационализируется с помощью подстановки:
 .
.
С учётом замены первоначальный интеграл примет вид:
 .
.
Выделяя целую часть в подынтегральном выражении, получим:

![]() .◄
.◄
2.6.4. Найти интеграл:
■ Подынтегральная функция нечётная относительно косинуса. Рационализируется интеграл с помощью подстановки:
![]() .
.
Исходный интеграл примет вид:

 .◄
.◄
2.6.5.
Найти интеграл:
■ Подынтегральная функция чётная относительно синуса и косинуса.
Применим подстановку:


 .
.
С учётом подстановки первоначальный интеграл примет вид:

 .
.
Подынтегральная
функция
 – рациональная дробь.
– рациональная дробь.
Разложим её на сумму простых дробей:
 .
.
![]() ;
;
Сгруппируем слагаемые с одинаковыми степенями при :
![]() .
.
Приравняем коэффициенты при одинаковых степенях .
![]()
![]()
.
Решим систему линейных уравнений:

Тогда первоначальный интеграл примет вид:


![]()

![]()


![]()
![]()
 .◄
.◄
2.6.6.
Найти интеграл:![]()
■ Подынтегральная функция чётная относительно синуса и косинуса.
Введём новую переменную:

С учётом подстановки первоначальный интеграл примет вид:

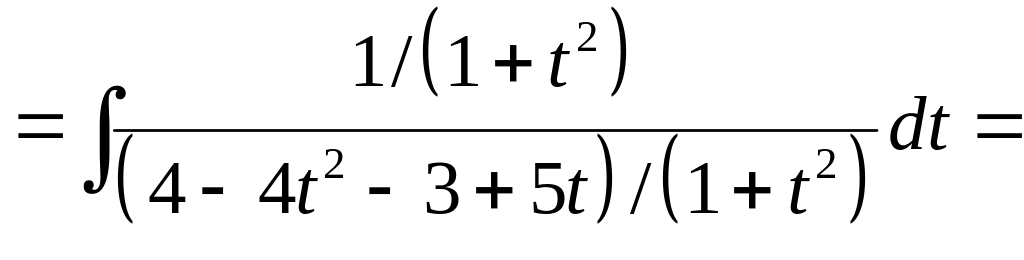

Выделим в знаменателе дроби неполный квадрат:

 .
.
Введём новую переменную:
![]()
Подставив в знаменатель дроби исходного интеграла неполный квадрат и новую переменную, получим:



 .◄
.◄
2.6.7.
Найти интеграл:![]()
■ Подынтегральная функция - нечётная относительно косинуса. Применим подстановку:

С учётом введения новой переменной исходный интеграл примет вид:



![]() .◄
.◄
2.6.8.
Найти интеграл:![]()
■ Подынтегральная функция - нечётная относительно косинуса и синуса.
Преобразуем её следующим образом:
 .
.
Введём новую переменную:
![]() .
.
С учётом этой замены первоначальный интеграл примет вид:

 .◄
.◄
2.6.9.
Найти интеграл:
■ Подынтегральная функция - нечётная относительно косинуса и тангенса.
Применим универсальную тригонометрическую подстановку:


С учётом подстановки первоначальный интеграл примет вид:



 .◄
.◄
