2.4. Интегрирование рациональных функций
Дробно-рациональной функцией (дробью) называется выражение вида
где
и
— многочлены степени
и
,
не имеющие общих корней, т.е.
Дробь называется
правильной если
;
неправильной в противном случае. Каждую
неправильную дробь можно привести к
правильной путем исключения целой
части, интегрирование которой не
представляет сложностей.
В курсе высшей алгебры доказывается теорема, о том, что любая правильная дробь может быть представлена в виде конечного числа простых дробей.
Если
— корни уравнения
,
а
— их соответствующие кратности, так
что
то дробь представляется в виде
где числители отдельных дробей определяются из системы линейных уравнений после приведения к общему знаменателю и приравнивания коэффициентов при одинаковых степенях с (метод неопределенных коэффициентов).
Если
— простые корни уравнения
,
т.е.
,
то
Если некоторые корни уравнения мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида
.
и методом
неопределенных коэффициентов найти
неизвестные
и
Таким образом, интегрирование правильной рациональной дроби приводится к интегралам вида
и
рассмотренных в предыдущем п.3.
Примеры:
2.4.1.
Найти интеграл:
.
1. В подынтегральном выражении
максимальная
степень при переменной в числителе
равна максимальной степени при переменной
в знаменателе. Поэтому подынтегральная
дробь – неправильная. Выполняя деление
на
,
получаем
следовательно,
.
2. Так как подынтегральная функция — правильная рациональная дробь, а корни её знаменателя являются вещественными и простыми (их кратность равна единице), то
,
откуда
.
Сравнивая
коэффициенты при
,
,
(свободные члены) в тождестве, получаем
систему
решение которой
,
,
.
Тогда,
.
2.4.2.
Найти интеграл:
Так как подынтегральная функция — правильная рациональная дробь, а корни её знаменателя являются вещественными, то представляя в виде суммы простых дробей
,
откуда
.()
Сравнивая
коэффициенты при
,
,
,
(свободные члены) в тождестве, получаем
систему
решение которой
.
Тогда
.
2.4.3.
Найти интеграл:
Подынтегральная функция — правильная дробь и представляя её в виде суммы простых дробей
,
откуда
,
и приравнивая коэффициенты при одинаковых степенях, получаем систему
решение которой
.
Тогда
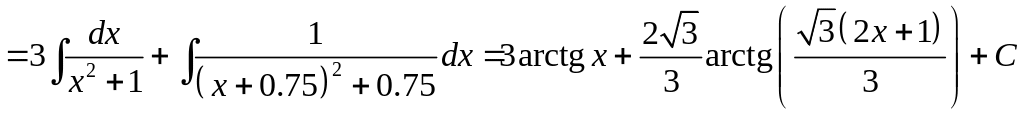
2.4.4.
Найти интеграл:
■ Подынтегральная функция – правильная рациональная дробь, знаменатель которой имеет различные действительные корни.
Представим её в виде суммы элементарных дробей:
.
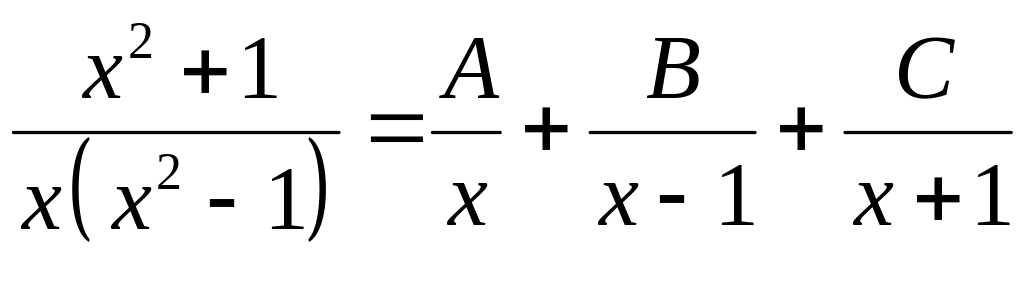Откуда:
;
Приравняем коэффициенты при одинаковых степенях и решим систему линейных уравнений:
Первоначальный интеграл примет вид:
.◄
2.5. Интегрирование иррациональных функций
2.5.1. Интегралы вида
где
— рациональные числа, приводятся к
интегралам от рациональных функций
подстановкой
где
общий знаменатель дробей
.
Примеры.
2.5.1.1.
Найти интеграл:
Положим
,
тогда
,
т. е.
;
Представляя
рациональную функцию
как сумму простsх
дробей, получим:
2.5.1.2.
Найти интеграл:
Положим
,
тогда
,
т. е.
.
Первоначальный интеграл примет вид:
.
2.5.1.3.
Найти интеграл:
Подынтегральную функцию преобразуем к виду:
.
Полагая
,
имеем:
,
,
,
тогда:
2.5.2. Интегралы вида
(интегралы от
биномиальных дифференциалов), где
— действительные числа, а
— рациональные, выражаются в элементарных
функциях только в следующих случаях:
(а) когда
— целое число; тогда этот интеграл
рационализируется подстановкой
,
где
- наименьшее общее кратное знаменателей
дробей
и
.
(б) когда
— целое число, то подстановкой
этот интеграл преобразуется к виду
В этом случае рационализация подынтегрального выражения осуществляется подстановкой
,
где
- знаменатель дроби
.
(в) когда
— целое число, то при помощи той же
подстановки
данный интеграл приводится к
Здесь мы будем использовать подстановку
.
Примеры:
2.5.2.1.
Найти интеграл:
.
■ В подынтегральном
выражении
– целое число.
Здесь случай (а). Применим подстановку:
;
.
Тогда
;
.
Здесь 6 – наименьшее общее кратное чисел
2 и 3.
Первоначальный интеграл примет вид:
.
И, наконец, переходя к первоначальной переменной , получим:
.◄
2.5.2.2.
Найти интеграл:
.
■ Преобразуем подынтегральную функцию следующим образом:
.
Тогда первоначальный интеграл примет вид:
.
-
целое число. Имеем место случай (a).
Применим подстановку:
;
т. е.
,
получим:
.
Откуда
;
.
Следовательно,
.
С учётом подстановки первоначальный интеграл примет вид:
Знаменатель подынтегральной дроби имеет действительные корни.
Разложим
подынтегральную функцию:
на сумму простых дробей:
.
Приведём к общему знаменателю и приравняем числители обеих частей уравнения:
;
Сгруппируем
слагаемые при одинаковых степенях
:
;
Приравняем коэффициенты при одинаковых степенях и решим систему уравнений:
Тогда исходный интеграл примет вид:
=
.◄
2.5.2.3.
Найти интеграл:
.
■ Преобразуем
подынтегральную функцию:
.
В интеграле
-
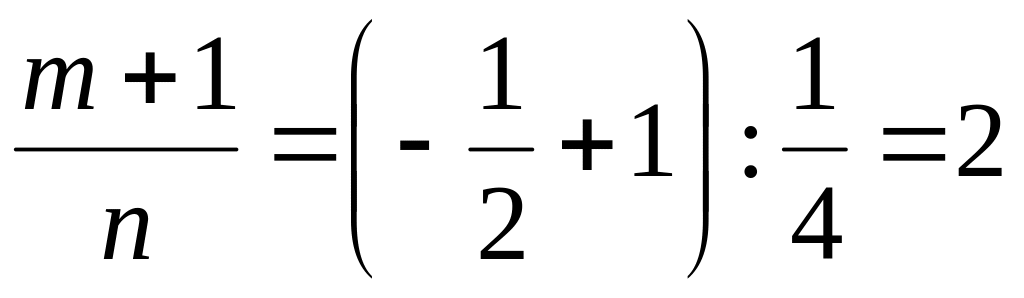целое число.
Имеем случай (б).
Применим подстановку Чебышева
или
.
Тогда
;
;
;
;
.
Тогда исходный интеграл примет вид:
.◄
2.5.2.4.
Найти интеграл:
Перепишем подынтегральное выражение в виде:
.
При
,
,
и
.
Очевидно, имеет место случай (в). Так как
,
то полагая
,
получаем
,
откуда
.
Следовательно,
.
2.5.2.5.
Найти интеграл:
Перепишем подынтегральное выражение в виде:
.
При
,
,
и
.
Очевидно, имеет место случай (в). Так как
,
то полагая
,
получаем
,
откуда
.
Следовательно,
2.5.2.6. Найти
интеграл:
■ Преобразуем подынтегральную функцию:
.
В интеграле
-
целое число. Имеем случай (б). Применим
подстановку Чебышева:
или
.
Тогда
;
Тогда исходный интеграл примет вид:
.
Перейдём к первоначальной переменной :
Так как , то
.◄
2.5.2.7.
Найти интеграл:
.
■ Преобразуем подынтегральную функцию:
.
Тогда исходный интеграл примет вид:
.
В интеграле
-
целое число. Имеем случай (б). Положим
или
.
Дифференцируя последнее равенство,
получаем:
.
Откуда:
.
С учётом замены первоначальный интеграл
примет вид:
.
Подынтегральная
функция
- рациональная дробь. Разложим знаменатель
дроби на множители:
.
Так как один корень знаменателя – действительный, а другой не является действительным, представим подынтегральную дробь в виде суммы простых дробей:
.
Приведём к общему знаменателю и приравняем числители обеих частей уравнения:
;
;
Сгруппируем слагаемые при одинаковых степенях :
.
Приравняем коэффициенты при одинаковых степенях .
.
Получим систему уравнений:
Следовательно,
.
Введём новую
переменную
,
.
Тогда интеграл примет вид:
.◄
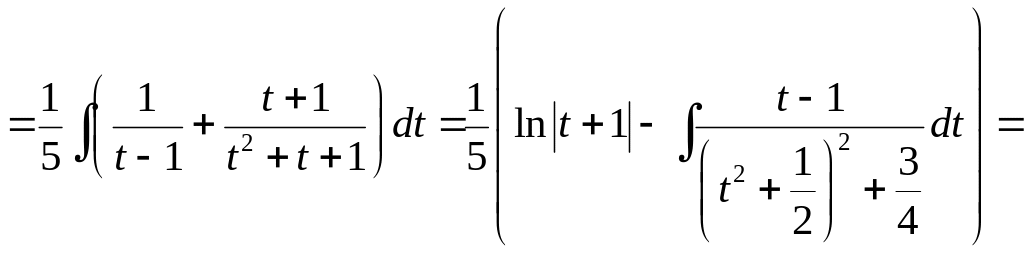
2.5.2.8. Рационализация подынтегрального выражения в интегралах вида
достигается с помощью, по крайней мере, одной из следующих трех подстановок, называемых подстановками Эйлера
(а)
при
;
(б)
при
;
(в)
при условии, что корни
и
уравнения
действительны.
Следует иметь в виду, что подстановки (а) – (в) часто приводят к громоздким вычислениям. Поэтому обычно применяют другие способы.
Заметим, что подынтегральную функцию можно представить в виде
,
где
и
- рациональные дроби. Записывая
в виде суммы многочлена
и суммы простых дробей, сведем интеграл
к линейной комбинации интегралов
следующих трех типов:
(а) 
;
(б) 
,
;
(в) 
,
,
.
При нахождении интеграла (а), где — многочлен степени , удобно использовать формулу
.
В этой формуле
— многочлен степени не выше
,
— некоторое число. Дифференцируя
тождество и умножая затем обе части
получаемого соотношения на
,
находим
.
Приравнивая коэффициенты при одинаковых степенях , вычислим коэффициенты многочлена и число . Интеграл в правой части сводится к табличному с помощью линейной подстановки.
Рассмотрим случай
(б). Подстановкой
этот интеграл сводится к интегралу
(а).
Рассмотрим интеграл
(в). Пусть существует число
такое, что для всех
выполняется равенство
,
т.е.
,
,
то интеграл (в) можно представить в виде
линейной комбинации интегралов
и 
.
Интеграл сводится к табличному, а интеграл подстановкой Абеля
сводится к интегралу от многочлена.
Если
,
то используется подстановка
,
где числа
и
подбираются такими, чтобы коэффициенты
при
в квадратных трехчленах подынтегральной
функции обратились в нуль. При этом
интеграл (в) примет вид
,
()
где
— многочлен степени
,
.
Если
,
но
,
то можно применить подстановку
.
Чтобы найти интеграл, разложим правильную рациональную дробь на простые дроби и представим интеграл в виде линейной комбинации интегралов вида
и 
.
Интеграл
вычисляется с помощью подстановки
,
а интеграл
— с помощью подстановки Абеля
.
Примеры:
2.5.1.
Найти интеграл:
Данный интеграл относится к случаю (а).
Полагаем
.
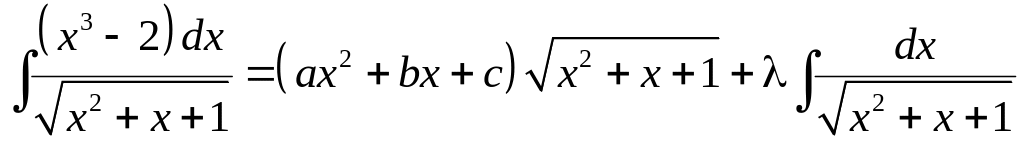Продифференцируем это тождество. Получим:
,
Откуда получаем:
Для нахождения
неопределённых коэффициентов
получим систему уравнений:
Откуда:
.
Следовательно,
2.5.2.
Найти интеграл:
Данный интеграл относится к случаю (б). Введём подстановку .
Тогда интеграл приводится к виду, рассмотренному в предыдущей задаче.
Положим
тогда
и для
имеем:
,
2.5.3.
Найти интеграл:
Данный интеграл относится к случаю (в).
Полагаем
,
Тогда:
,
Откуда:
.
Дифференцируя
равенство
,
получим:
,
Откуда:
.
Итак,
.
Поэтому:
.
2.5.4.
Найти интеграл
.
Данный интеграл
относится к (в), причём
.
Положим
.
Подберём числа
и
так, чтобы коэффициенты при
в квадратных трехчленах подынтегральной
функции обратились в нуль. Так как
,
,
то, приравнивая к нулю коэффициенты при в числителях этих дробей, получаем систему
решение которой
,
.
Следовательно,
искомая замена
.
Тогда имеем
,
,
числитель преобразуется как
, 
,
а сам интеграл
,
где
и 
.
Интеграл
вычисляется при помощи замены
.
Тогда,
,
.
То есть, вычисление интеграла
сводится к табличному
.
Для вычисления
сделаем подстановку
или
.
Дифференцируя, получаем
,
а с учётом подстановки
или
.
Кроме того, из
следует
.
Таким образом, вычисление
сводится к табличному
.
Объединяя вычисления, окончательно получаем
,
где
.