Пример 5. Расчет уголковой подпорной стены (с нагрузкой от подвижного транспорта)

Дано. Сборно-монолитная железобетонная подпорная стена уголкового профиля (УПС). Высота подпора грунта у = 4,5 м, глубина заложения подошвы фундамента d = 1,2 м. На поверхности призмы обрушения вдоль стены перемещается тяжелая одиночная нагрузка НГ-60 на расстояние 1,5 м от наружной грани стены. Геометрические размеры подпорной стены и схема ее загружения приведены на рис. 12. Основание подпорной стены - глинистые грунты ненарушенного сложения со следующими характеристиками (по данным инженерно-геологических исследований):

_I = 16; _I = 16 кН/м³; с_I = 21 кПа;

_II = 17; _II = 16 кН/м³; с_II = 24 кПа.

Характеристики грунта засыпки - песок мелкий:

_I = 30; _I = 20,9 кН/м³; с_I = 0;

_II = 32; _II = 20,9 кН/м³; с_II = 0.

Под подошвой фундамента подпорной стены предусматривается щебеночная подушка толщиной 0,6 м и шириной 4,2 м (на 300 мм больше подошвы фундамента в каждую сторону), имеющая следующие характеристики:

_I(s) = _II(s) = 40; с_I(S) = c_II(s) = 0; _I(s) = 21 кН/м³.

Требуется проверить принятые габаритные размеры, определить величину изгибающих моментов и поперечных сил в элементах конструкций.

Определяем интенсивность давления грунта на конструкцию стены.

Угол наклона плоскости скольжения к вертикали:

;

₀ = 30.

Условный угол плоскости обрушения грунта принимаем:

tg  = 3/5,7 = 0,526;  = 2748  28.

По табл. 3. прил. 2 (при  = _I = 30;  = 0;  = 28)  = 0,33.

Эквивалентную распределенную полосовую нагрузку на поверхности засыпки от гусеничной нагрузки НГ-60 определяем по формуле (13)

q = 90/(2,5 + y_a tg₀) = 90/(2,5 + 1,35 tg 30) = 27,44 кПа.

Расстояние по вертикали от поверхности грунта засыпки до границ распределения условной эквивалентной боковой нагрузки определяем по формуле

у_а = а/(tg ₀ + tg ) = 1,5/(tg 30+ tg28) = 1,35 м.

Протяжность эпюры давления определяем по формуле

у_b = (b₀ + 2tg ₀у_х)/(tg  + tg ₀) = (3,3 + 2tg301,35)/(tg 28+ tg30) = 4,38 м.

В соответствии с п. 5.7б принимаем:

y_b = h - y_a = 5,7 - 1,35 = 4,35 м.

Интенсивность горизонтального давления грунта на глубине у = 5,7 м, определяем по формуле (1)

кПа.

Интенсивность горизонтального давления грунта от условной эквивалентной полосовой нагрузки определяем по формуле (10)

кПа.

Расчет устойчивости положения стены против сдвига

Сдвигающую силу F_s определяем по формулам (16), (17), (18):

F_s = P_h/2 = 45,215,7/2 = 128,85 кН;

F_{s, q} = P_qy_b = 6,154,35 = 26,75 кН;

F_s = F_{s, } + F_{s, q} = 128,85 + 26,75 = 155,6 кН.

Проверка устойчивости стены против сдвига (рис. 13) производится для трех случаев скольжения:

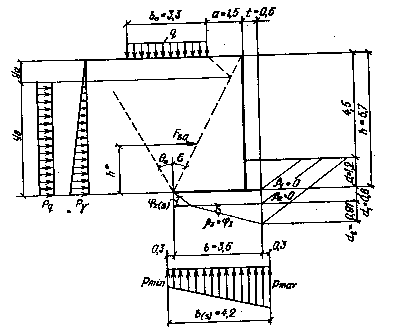
Рис. 13. Расчетная схема подпорной стены к примеру 5

1. Проверка устойчивости стены по контакту подошвы и щебеночной подушки - ₁ = 0 (рис. 13).

Сумму проекций всех сил на вертикальную плоскость определяем по формуле (21)

F_ = F_s tg( + _I^') + _I^'_f[h(b - t)/2 + td] +_I tg₁b²/2 = 155,6 tg(28 +30) + +20,91,2[5,7(3,6 - 0,6)/2 +0,61,2] + 0 = 481,56 кН.

Пассивное сопротивление грунта определяем по формуле (22)

E_r = _Ih_r²_r/2 + c_Ih_r(_r - 1)/ tg_I = 20,912²1/2 + 0 = 15,05 кН.

Удерживающую силу F_sr определяем по формуле (19), с учетом п. 6.7, _I(s) = 30, _r = 1.

F_sr = F_ tg(_I(s) - _I) + bc + E_r = 481,56 tg(30 - 0) + 0 + 15,05 = 293,1 кН.

Проверяем условие (15):

F_s = 155,6 кН < 0,9293,1/1,1 = 239,81 кН.

Условие удовлетворено.

2. Проверка устойчивости стены против сдвига по контакту щебеночной подушки и грунта основания (₂ = 0).

F_(s) =F_ + b_(s)d_I_I(s) = 481,56 + 4,20,621 = 534,48 кН;

E_r(s) = 20,9(1,2 + 0,6)²1/2 + 0 = 33,86 кН;

F_sr(s) = 534,48 tg(16 - 0) + 0 33,86 = 187,1 кН.

Проверяем условие (15):

F_s = 155,6 кН < 0,9187,1/1,1 = 153,08 кН.

Условие удовлетворено.

3. Проверка устойчивости стены по плоскости глубинного сдвига грунта основания (₃ = _I = 16).

E_r = _Ih_r²_r/2 + c_Ih_r(_r - 1)/tg_I = 16(1,2 + 0,6 + 0,91)²1,76/2 + 21(1,2 + +0,6 + 0,91)(1,76 - 1)/tg16 = 254,26 кН;

_r = tg²(45 + _I/2) = tg²(45 +16/2) = 1,76;

F_sr = F_ tg(_I - ₃) + bc_I + E_r = 0 + 3,621 + 254,26 = 329,86 кН.

Проверяем условие (15):

F_s = 155,6 кН < 0,9329,86/1,1 = 269,89 кН.

Условие удовлетворено.

Приведенный угол наклона к вертикали _I равнодействующей внешней нагрузки по контакту подошвы и щебеночной подушки:

tg_I = F_s /F_ = 155,6/481,56 = 0,3231; _I = 18.

sin_I(s) = sin40 = 0,642 > tg_I,

расчет прочности основания производим по формуле (26)

h* = [F_s, h/3 + F_s,q(h - y_ - y_b/2)]/F_s = [128,855,7/3 + 26,75(5,7 - 1,35 - -4,35/2)]/155,6 = 1,95 м;

M₀ = F_s[h* - tg( + _I^')(b/2 - h*tg)] + _I^'_f(b - t)[h(b - 4t) + 6td]/12 = 155,6[1,95 - tg (28 + 30) (3,6/2 - 1,95tg28] + 20,91,2(3,6 - 0,6)[5,7(3,6 - -40,6) +60,61,2]/12 = 183,4 кНм;

e = M₀/F_ = 183,4/481,56 = 0,38 м;

b^' = b - 2e = 3,6 - 20,38 = 2,84 м.

По табл. 5 при _I = 30 и _I = 18; N_ = 3,35; N_q = 8,92; N_c = 13,72; N_u= b^'(N_b^'_I + N_q_I^'d + N_cc_(s)) = 2,84(3,352,8421 + 8,9220,91,2 + 0) = =1202,75 кН;

F_ = 481,56 кН < _cN_u/_n = 0,91202,75/1,1 = 984,07 кН.

Несущая способность щебеночной подушки под подошвой фундамента стены обеспечена.