30.Переменный ток. Характеристики переменного тока. Резистор в цепи переменного тока.
Переменный ток — электрический ток, который периодически изменяется по величине и направлению.
Закон
изменения : 
- максимальное значение
Характеристики переменного тока:
Средняя
мощность переменного тока за период T
равна:
где f - сдвиг фаз между током и
напряжением, Um и Im - максимальные
(амплитудные) значения напряжения и
силы тока.
Активная мощность:
- мгновенная мощность
Реактивная мощность:
действующие значения
напряжения и тока,
- угол сдвига фаз между ними.
Период – время одного цикла изменения
тока по направлению и числовому значению
(T, c).
Частота – это число циклов
изменения тока в единицу времени. n =1/Т
(величина обратная периоду с-1, Гц)
Круговая частота (
,
2p/Т радиан/с)
Фаза (j) – это
величина, определяющая во времени
взаимоотношение тока и напряжения в
электрической цепи.
Мгновенное
значение тока и напряжения - значение
этих величин в данный момент времени
(i, u).
31.Конденсатор
и емкость в цепи переменного тока.
Емкостное и индуктивное
сопротивление.
Конденсатор
- устройство для накопления энергии
электрического поля. Конденсатор
является пассивным электронным
компонентом. Обычно состоит из двух
электродов в форме пластин (называемых
обкладками), разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок.
Ёмкость плоского
конденсатора, состоящего из двух
параллельных металлических пластин
площадью
каждая,
расположенных на расстоянии
друг
от друга, в системе СИ
выражается формулой:
,
где
—
относительная диэлектрическая
проницаемость среды, заполняющей
пространство между пластинами (в вакууме
равна единица),
—
электрическая постоянная
При
параллельном соединении емкость равна:
или
При последовательном соединении емкость равна:
или
Если конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном то в другом направлении.
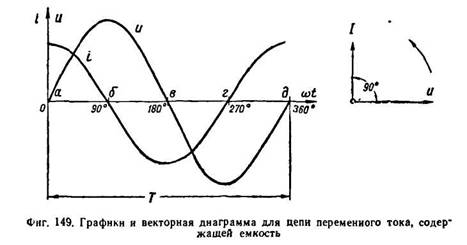Если
включить конденсатор к переменному
напряжению сети, то в течение первой
четверти периода, когда напряжение сети
будет возрастать, конденсатор будет
заряжаться.
По мере накопления зарядов
на обкладках конденсатора напряжение
конденсатора увеличивается. Когда
напряжение сети к концу первой четверти
периода достигнет максимума, заряд
конденсатора прекращается и ток в цепи
становится равным нулю.
Ток в цепи
конденсатора можно определить по
формуле:
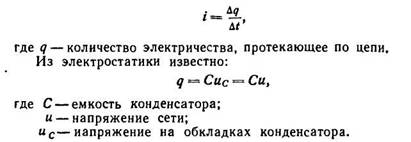
Окончательно для
тока имеем:
Индуктивное сопротивление:
Рассмотрим, что происходит в цепи, содержащей резистор и катушку индуктивности. Колебания силы тока, протекающего через катушку:
вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:
т.е. колебания напряжения опережают по фазе колебания силы тока на p /2. Произведение w LIm является амплитудой колебания напряжения:
Произведение циклической частоты на индуктивность называют индуктивным сопротивлением катушки:
поэтому связь между амплитудами напряжения и тока на катушке совпадает по форме с законом Ома для участка цепи постоянного тока:
Емкостное сопротивление:
При изменении
напряжения на обкладках конденсатора
по гармоническому закону:
заряд q на его обкладках изменяется также по гармоническому закону:
.
Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:
Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на p /2. Произведение w CUm является амплитудой колебаний силы тока:
Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:
(3)
Для конденсатора
получаем соотношение, аналогичное
закону Ома:
(4)
32. Последовательное
соединение R, L, C в цепи переменного тока.
Резонанс напряжений.
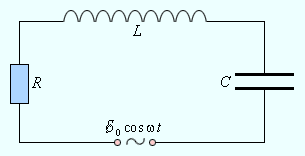Для
мгновенных значений токов и напряжений
можно записать закон Ома:
Величина 
– это ЭДС
самоиндукции катушки,
перенесенная с изменением знака из
правой части уравнения в левую. Эту
величину принято называть напряжением
на катушке индуктивности.
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений. Соотношения выражают закон Ома для участка цепи переменного тока, содержащего один из элементов: R, L и C.
Особенности
полной цепи:
1.
Соблюдается закон Ома
2. Полная цепь
оказывает переменному току сопротивление.
Это сопротивление называется полным
(мнимым, кажущимся) или импедансом.
3.
Импеданс зависит от сопротивления всех
элементов цепи, обозначается Z и
вычисляется не простым, а геометрическим
(векторным) суммированием. Для
последовательно соединенных элементов
формула импеданса имеет следующее
значение:
здесь:
Z
- импеданс последовательной цепи, R -
активное сопротивление,
–
индуктивное
и
–
ёмкостное сопротивление,
Так
как ёмкостное и индуктивное сопротивления
дают для напряжения сдвиг фаз в
противоположном направлении, возможен
случай, когда
=
.
При этом алгебраическая сумма модулей
будет равна нулю, а импеданс – наименьшим.
Состояние,
при котором в цепи переменного тока
ёмкостное сопротивление равно
индуктивному, называется резонансом
напряжения.
Частота, при которой
=
,
называется резонансной частотой. Эту
частоту можно определить по формуле
Томсона:
Напряжения на участках:
Активная мощность:
P = R I2 = U1 I
Реактивные мощности: QL = XL
I2 ; QC = XC I2
Полная мощность цепи:
33. Параллельное соединение R, L ,C в цепи переменного тока. Резонанс токов. ЧАСТИЧНО ЭТОТ ВОПРОС НАПИСАН В ПРЕДЫДУЩЕМ
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений. Соотношения выражают закон Ома для участка цепи переменного тока, содержащего один из элементов: R, L и C.
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока
При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока.
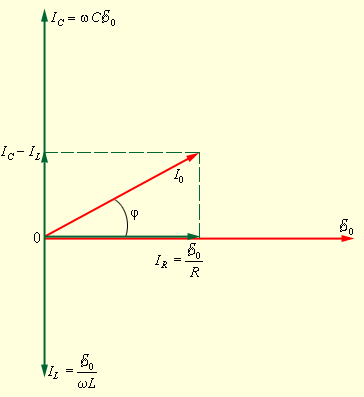
Из диаграммы следует:
|
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением
|
При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:
Z = Zmax = R. |
Фазовый сдвиг φ
между током и напряжением при параллельном
резонансе равен нулю.
Явление
возрастания амплитуды колебаний тока
при совпадении частоты ω колебаний
внешнего источника с собственной
частотой ω0 электрической цепи называется
электрическим резонансом. При резонансе
Сдвиг
фаз φ между приложенным напряжением и
током в цепи при резонансе обращается
в нуль. Резонанс в последовательной
RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).
34. Работа и
мощность в цепи переменного тока.
Работа
переменного тока:
Мощность
Мгновенная
мощность
воспользовавшись формулой
приведем предыдущую хуйню к виду (забодай
меня комар... сейчас будет невъебаться
здоровая формула)
Практический
интерес представляет средняя по времени
моoность P (хотя лично меня и она не особо
волнует)
так как среднее значение 
Таким
образом, мгновенная мощность колеблется
возле среднего значения с частотой
,
в 2 раза превышающей частоту тока,
нах.
Путем хитрых преобразований
(или проще говоря "из этого всего
ЭЛЕМЕНТАРНО получается")
где 
- коэффициент мощности
35. Символическое
представление токов и напряжений.
Комплексное сопротивление.
Расчеты
цепей переменного тока значительно
упрощаются, если применять так называемый
символический метод. Этот метод
основывается на том, что, как известно
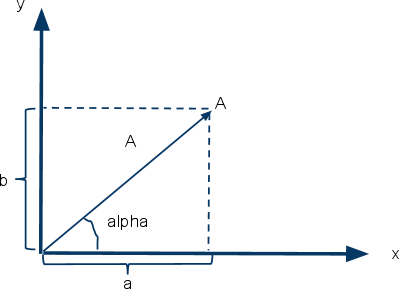
из курса математики, каждому вектору
А, расположенному в координатной
плоскости, можно сопоставить
комплексное число
где a,b - проекции вектора на оси, А - модуль
комплексного числа (совпадающий с
модулем вектора) нах,
-
аргумент комплексного числа (совпадающий
между вектором и осью х), j - мнимая
единица.
ИТАААААК:
Между
величинами a,b,A и
имеется
следующее отношение
(это все системой)
При
сложении комплексных чисел отдельно
складываются целые и мнимые части
вычислим
падения напрядения на индуктивности и
емкости
Падение
напряжения на индуктивности:
тогда
то
Падение
напряжения на екости:
тогда
Падение
напряжения на сопротивлении:
Комплексное
сопротивление:
его модуль равен полному сопротивлению,
а аргумент равен
-
сдвигу фаз между напряжением и током.
Следовательно
