25. Гармонические колебания. Амплитуда, круговая частота, фаза колебаний. График гармонического колебательного движения. Уравнение и решение гармонического колебательного движения.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.

Уравнение: или ,где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая(круговая) частота колебаний,  — полная фаза колебаний,  — начальная фаза колебаний.

Амплитудой колебаний называют наибольшее отклонение колеблющегося тела от его первоначального (спокойного) положения. Чем больше амплитуда колебания, тем громче звук.

Круговая частота (синонимы: радиальная частота, циклическая частота, угловая частота) — скалярная величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, круговая частота равна модулю вектора угловой скорости. Угловая частота является производной по времени от фазы колебания:

Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода):  1 цикл =    радиан = 360°

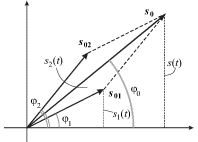
26. Метод векторных диаграмм. Сложение одинаково направленных колебаний одной частоты. Метод векторных диаграмм заключается в том, что колебание можно изобразить в виде вращения вектора

   где - угол, совпадающий с начальной фазой. - скорость вращения вектора, равная частоте колебаний длина вектора равна амплитуде колебаний (A). Сложение одинаково направленных колебаний: S мысленно меняем на A :  

        :  если               если                  

27.Сложение взаимно перпендикулярных колебаний одной частоты о_О ^_^  *сука_блять_няшный_смайл_нах*

          Наиболее простой вид имеет уравнение движения, если тело участвует в двух взаимно перпендикулярных колебательных движениях с одинаковыми частотами . Тогда уравнения горизонтальных и вертикальных колебаний примут вид:

    

           Воспользовавшись тригонометрическими тождествами, приведем уравнения колебаний к виду

                                                    

           Из первого уравнения следует, что

                                                     

                                                        Подставляя полученные выражения во второе уравнение, и возводя его в квадрат, не трудно получить уравнение траектории в виде                                                                   Уравнение траектории описывается уравнением эллипса. То есть траектория результирующего колебания имеет форму эллипса. Такие колебания называются эллиптически поляризованными. Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз  .            Например, когда разность фаз кратна , эллипс вырождается в отрезок прямой  для нечетных m или  (табл.1: ωx :ωy = 1:1, ϕ = 0, ±π). Результирующее колебание является гармоническим – тело совершает гармонические колебания вдоль прямой с амплитудой  . Такие колебания называются линейно поляризованными.              В случае, когда разность фаз кратна  траектория принимает форму эллипса, приведенного к осям координат (оси эллипса совпадают с осями координат). Когда амплитуды вертикальных и горизонтальных колебаний равны , эллипс вырождается в окружность. Такие колебания называются поляризованными по кругу.

28. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Время релаксации. Логарифмический декремент затухания. Дифференциальное уравнение принимает вид

Сделав замену x = eλt, получают характеристическое уравнение 

Корни которого вычисляются по следующей формуле

;

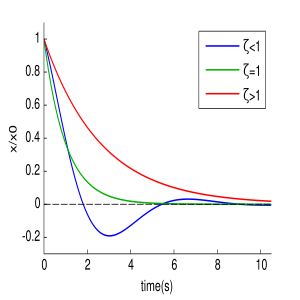
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.     

Апериодичность

Если , то имеется два действительных корня, и решение дифференциального уравнения принимает вид: В этом случае колебания с самого начала экспоненциально затухают.

Граница апериодичности

Если , два действительных корня совпадают , и решением уравнения является: В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.

Слабое затухание

Если , то решением характеристического уравнения являются два комплексно сопряжённых корня

Тогда решением исходного дифференциального уравнения является

Где    — собственная частота затухающих колебаний.

Константы c1 и c2 в каждом из случаев определяются из начальных условий:

Релаксация — многоступенчатый процесс, т. к. не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и др.) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, т. е. производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.

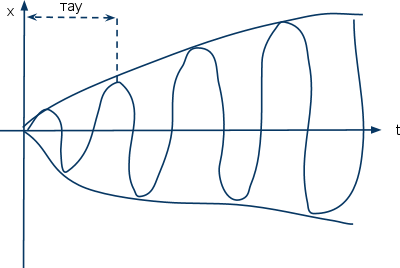
29. Вынужденные колебания. Резонанс Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

                       

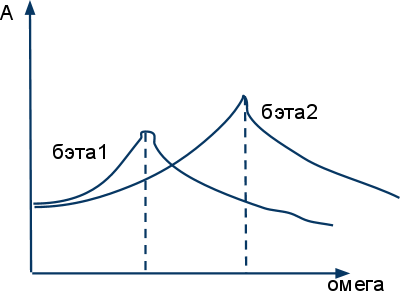
                            Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при стремлении частоты собственных колебаний к вынужденным.