2.Устойчивость линейных систем. Критерий устойчивости Найквис­та.

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения сист. отклонилась от состояния равновесия и после прекращения действия внеш. возмущения снова вернулась в исх. состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необх. и дост. условие уст-ти является выполнение требования, в соот-ии с которым характ-ое уравнение сист. должно иметь отриц. вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы. Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы. Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.

Критерий устойчивости Найквиста.

-сформулирован в 1932 году.

Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы.

Пример:

Билет №13

1. Передаточная функция системы, соединенных между собой звеньев.

Передаточная функция системы это отношение преоб-ния Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при начальных нулевых условиях.

W(s)=X(s)/G(s), s=p – показатель дифференцирования

Последовательное соединение - выходная величина предшествующего звена подается на вход послед-щего.

, ,

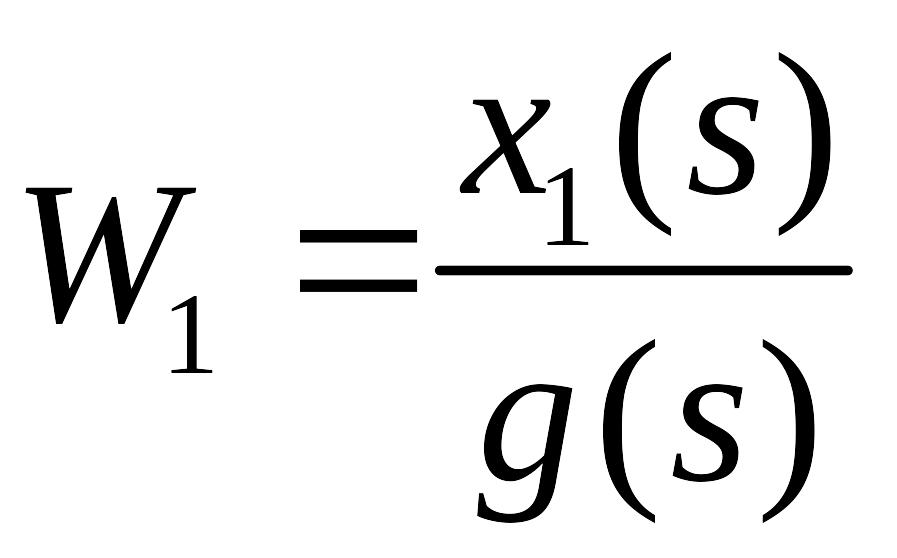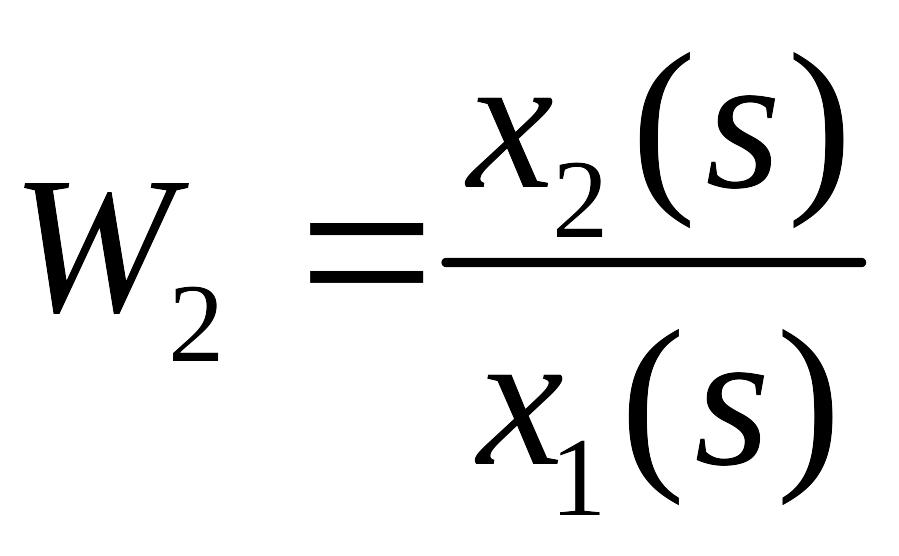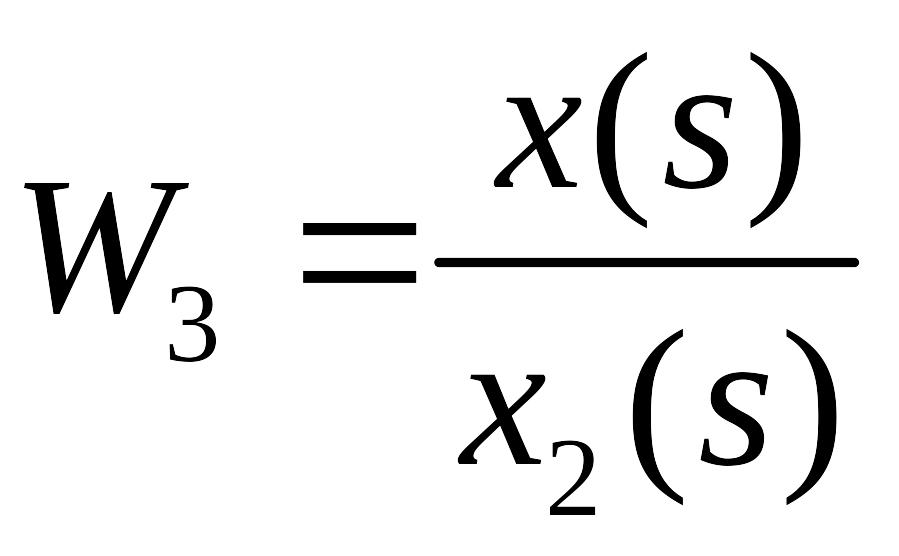
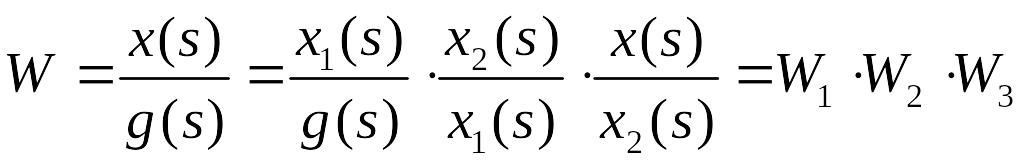
То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев.

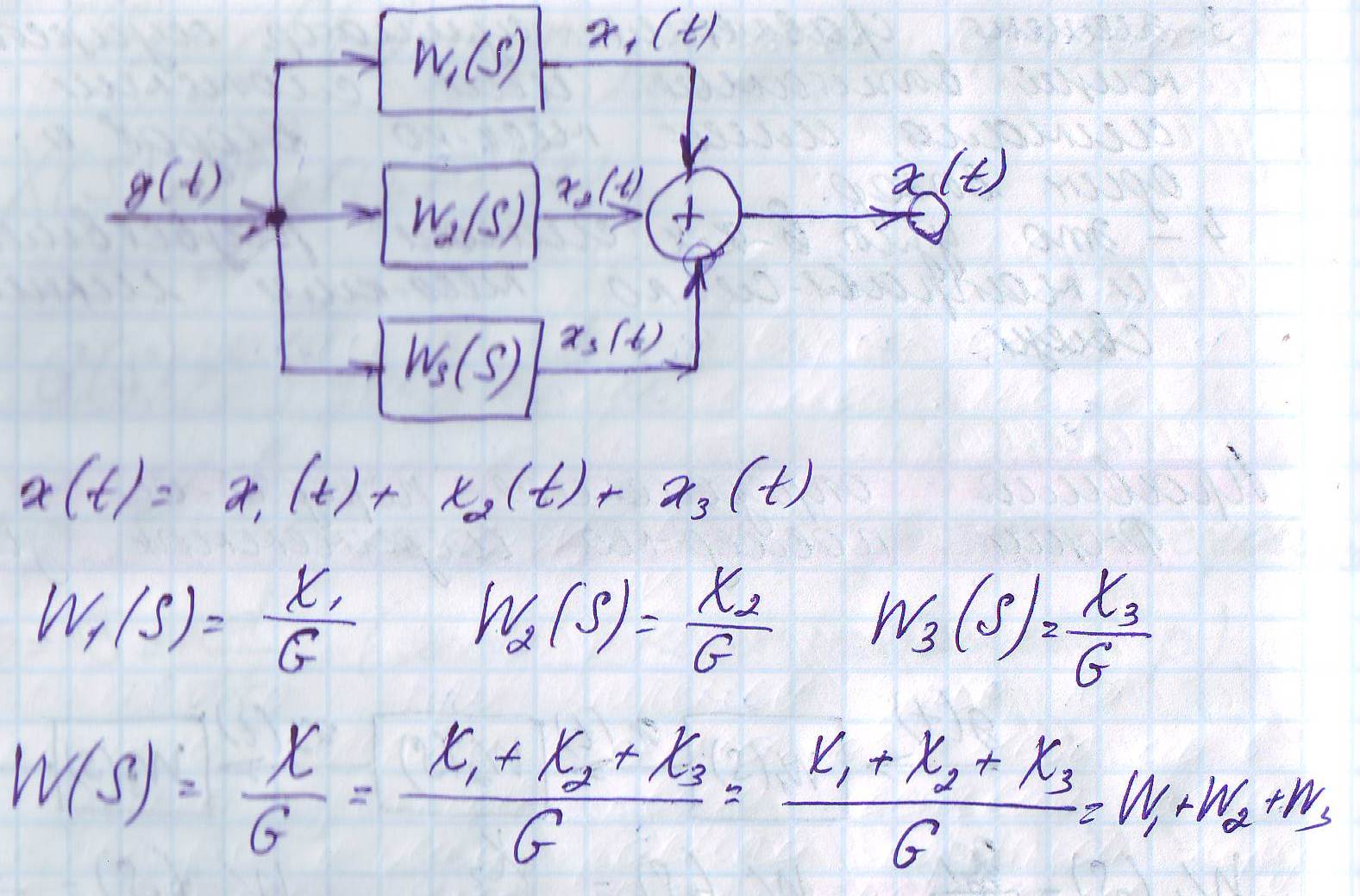
Правило определения перед-й функции параллельного соединения звеньев: перед-я функция парал-но соединенных звеньев равна произведению перед-х функций этих звеньев.

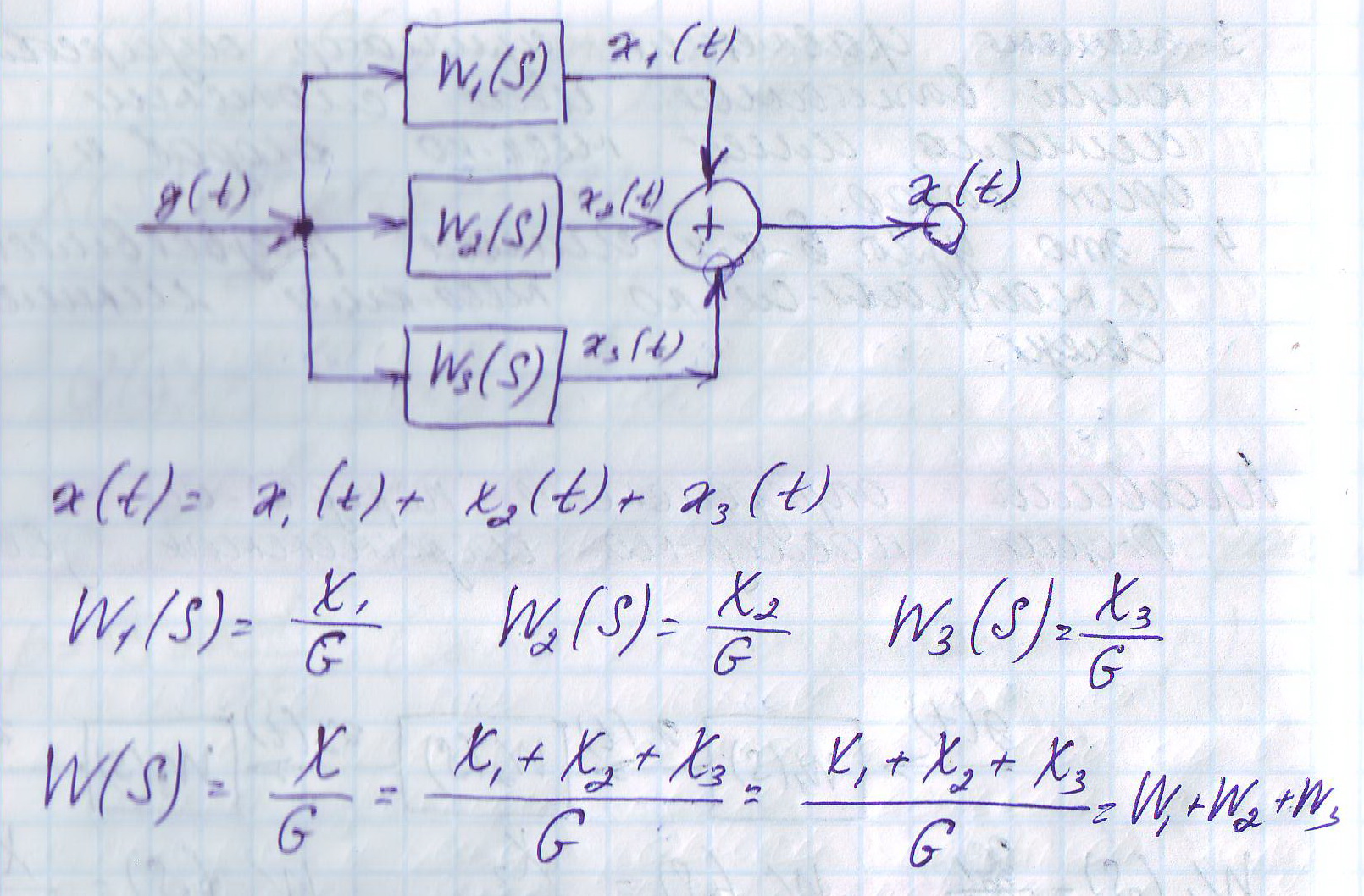
2. Устойчивость линейных систем. Критерий Раусса-Гурвица.

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения сист. отклонилась от состояния равновесия и после прекращения действия внеш. возмущения снова вернулась в исх. состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необх. и дост. условие уст-ти является выполнение требования, в соот-ии с которым характ-ое уравнение сист. должно иметь отриц. вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы. Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы. Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.

Критерий устойчивости Раусса-Гурвица

Необх. и дост. усл-ем уст-ти системы любого порядка без решения характ-го уравнения, по рассмотрению его коэфф-ов, были сформулированы учеными Раусом и Гурвицом.

Руас сказал, что для выполнения условия устойчивости, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

Гурвец дополнил, что для выполнения условия устойчивости, необходимо и достаточно, чтобы все n диагональных миноров определителя характеристического ур-я были положительны.

Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей характ-го уравнения сводится к выполнению общих алгебраических операций.

Билет №14

1.Структурные схемы и их преобразование. Последовательное соединение звеньев.

2. Построение логарифмических характеристик последовательно соединенных типовых звеньев.

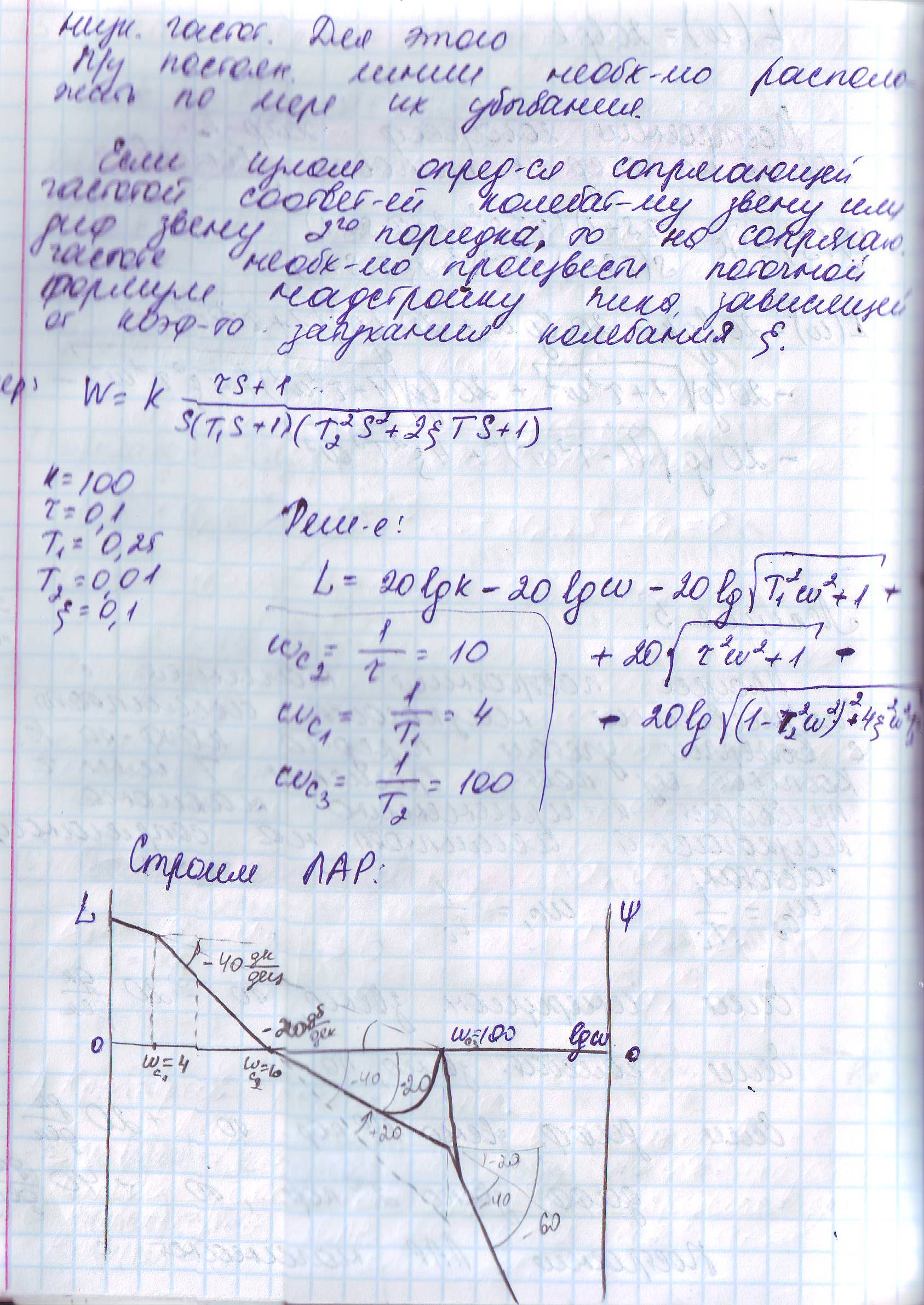
Билет №15

1. Структурные схемы и их преобразование. Параллельное соединение звеньев.

2. Типовые звенья. Безинерционное звено.

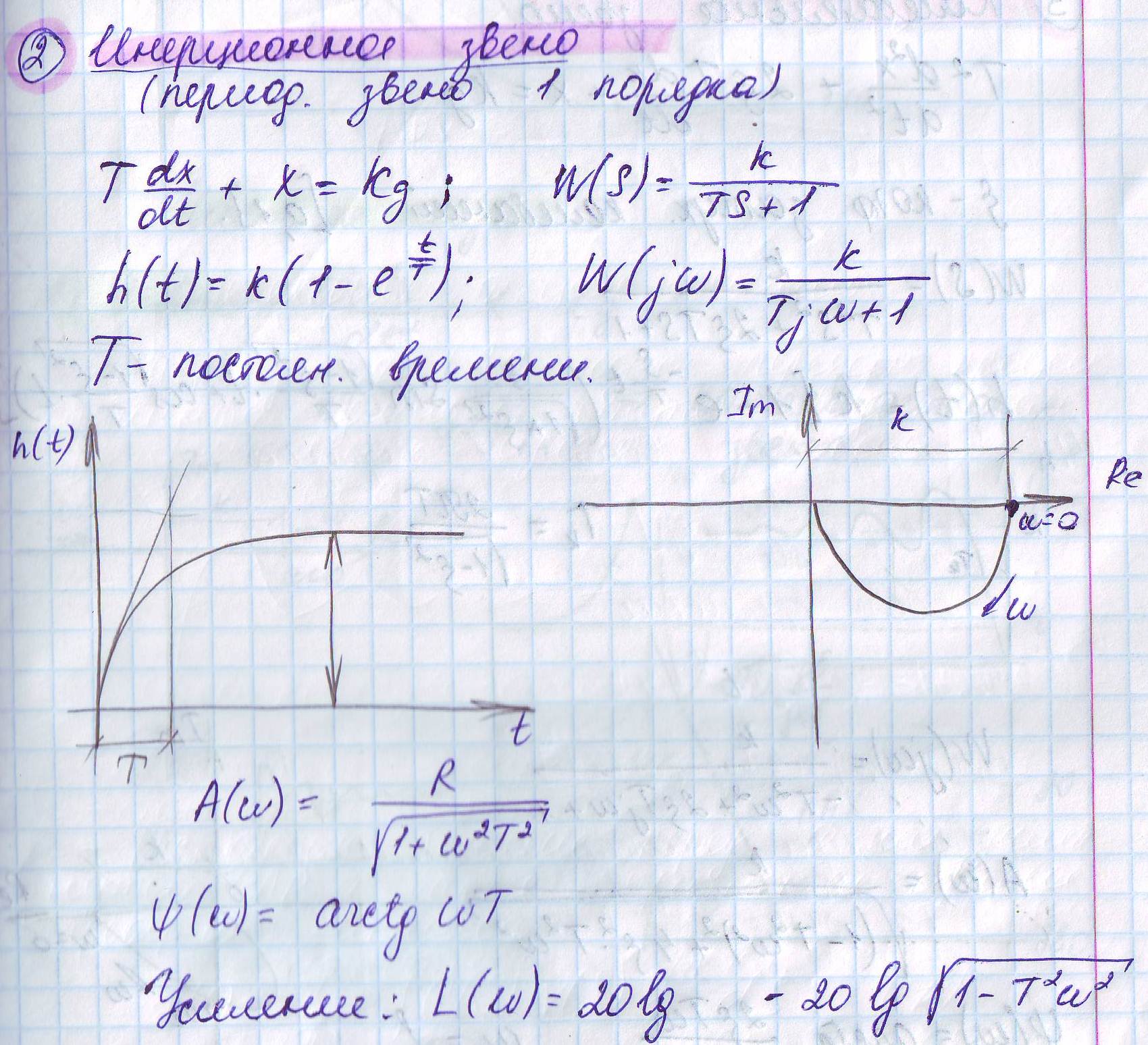
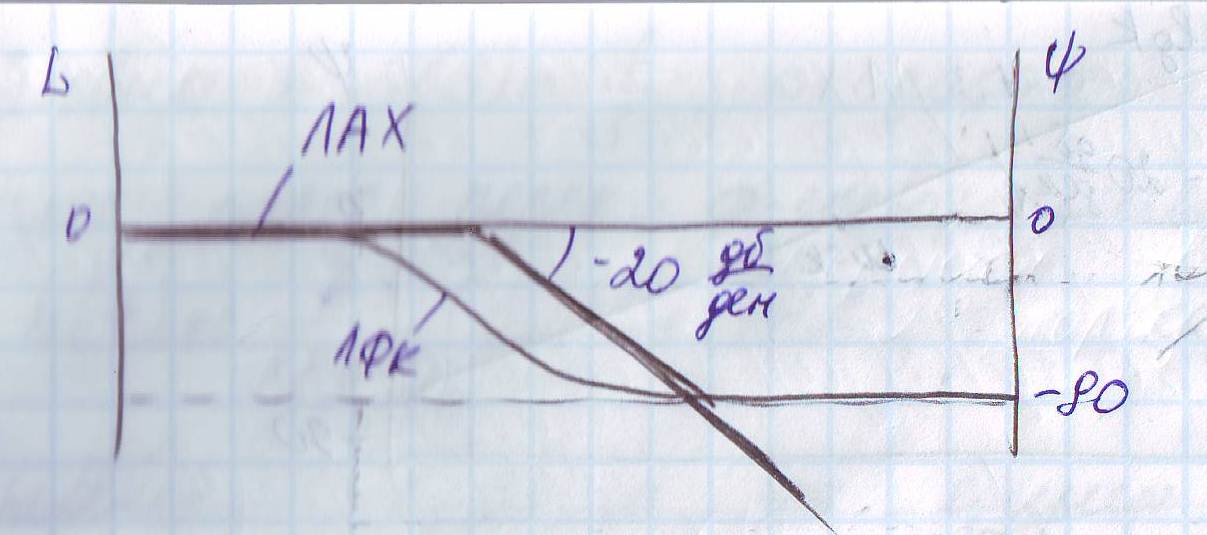
Билет №16

1. Структурные схемы и их преобразования. Неединичная и единичная обратная связь. (смотри билет 15)

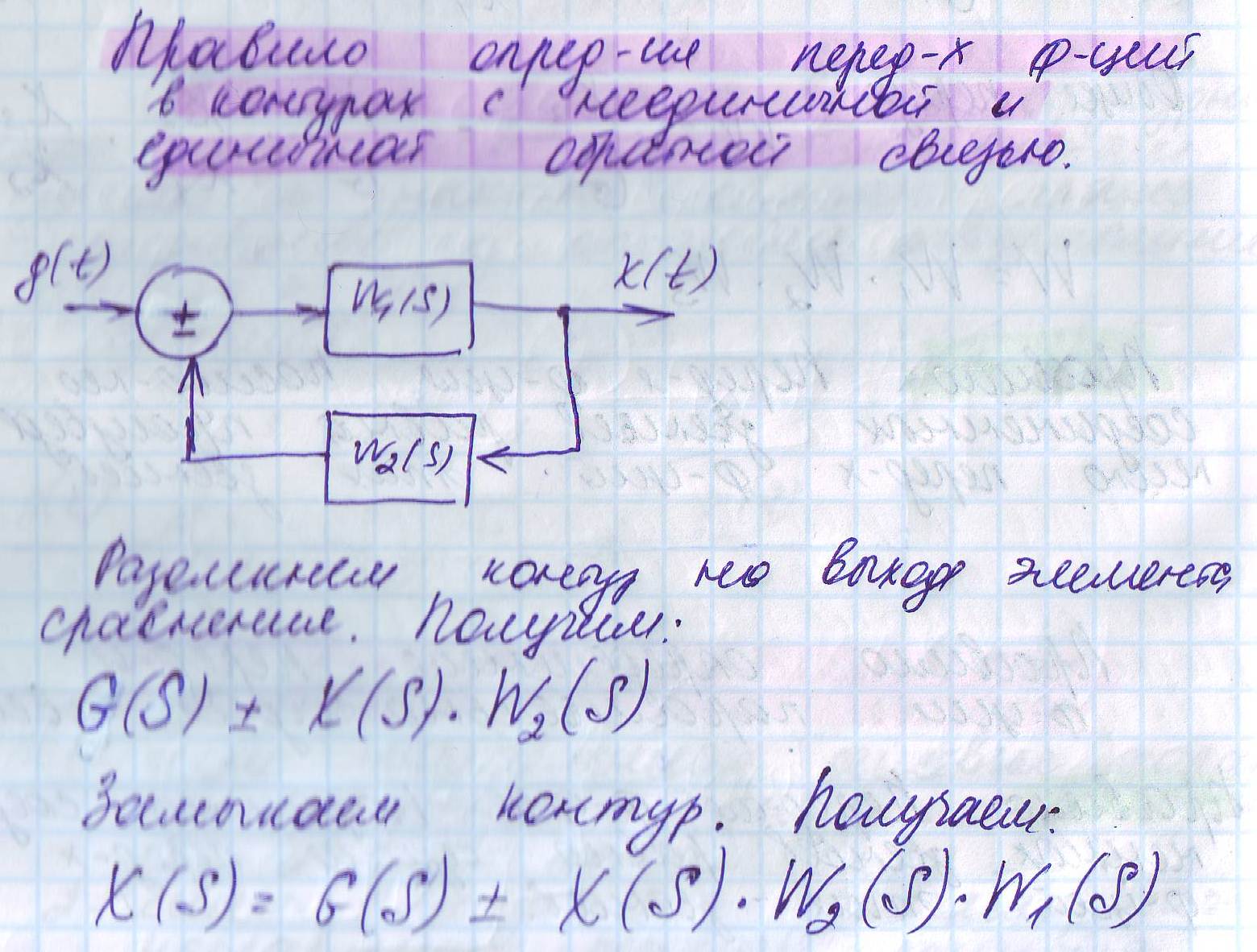
2. Типовые звенья.

Типовые звенья делятся на:

1) Идеально интегрирующее звено

2) Инерционное звено

3) Колебательное звено

4) Дифференциальное звено 1-го порядка

5) Дифференциальное звено 2-го порядка

6) Усилительное звено

Дифференциальное звено 2-го порядка.

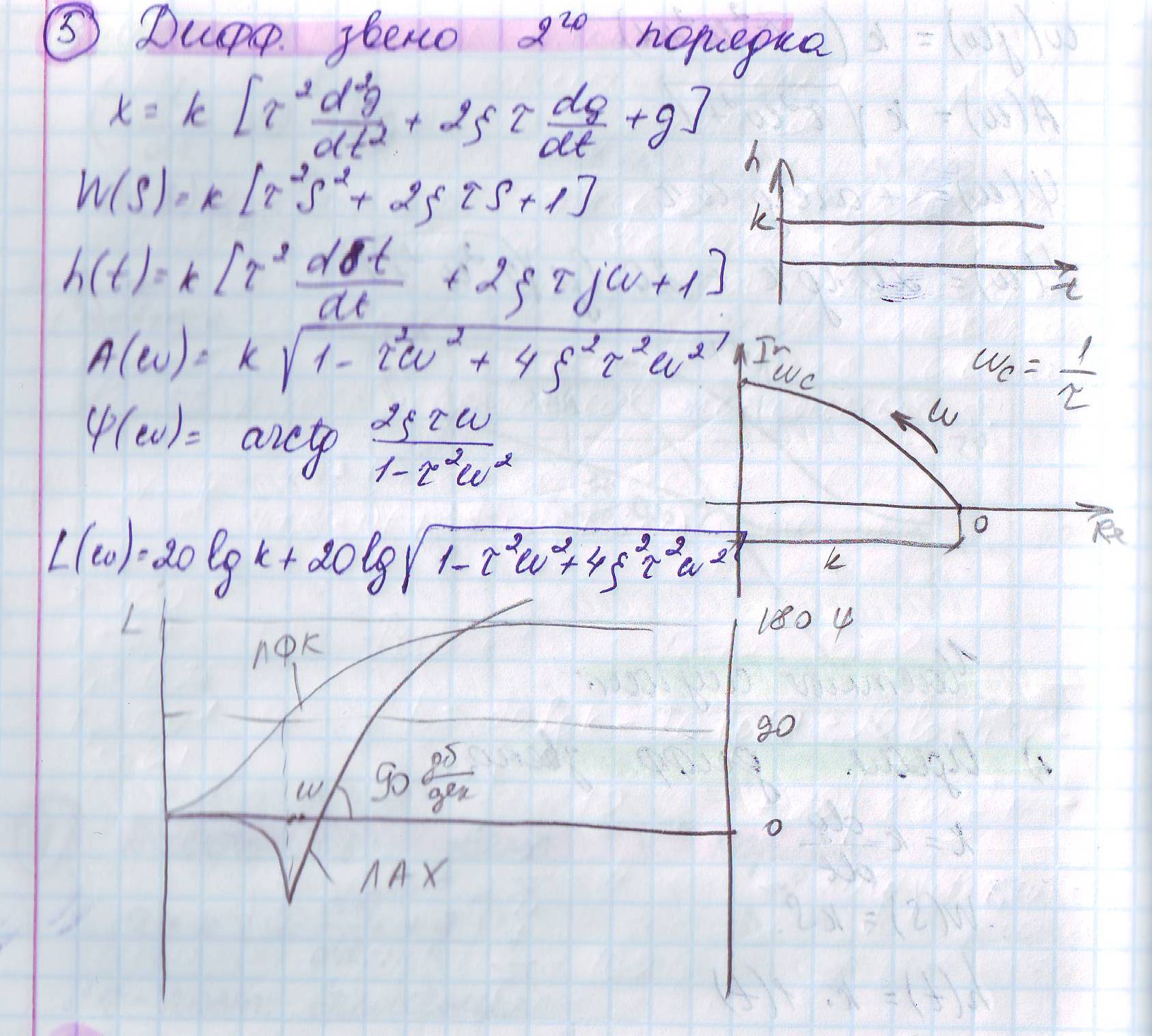
Билет №17

1. Правило переноса узла

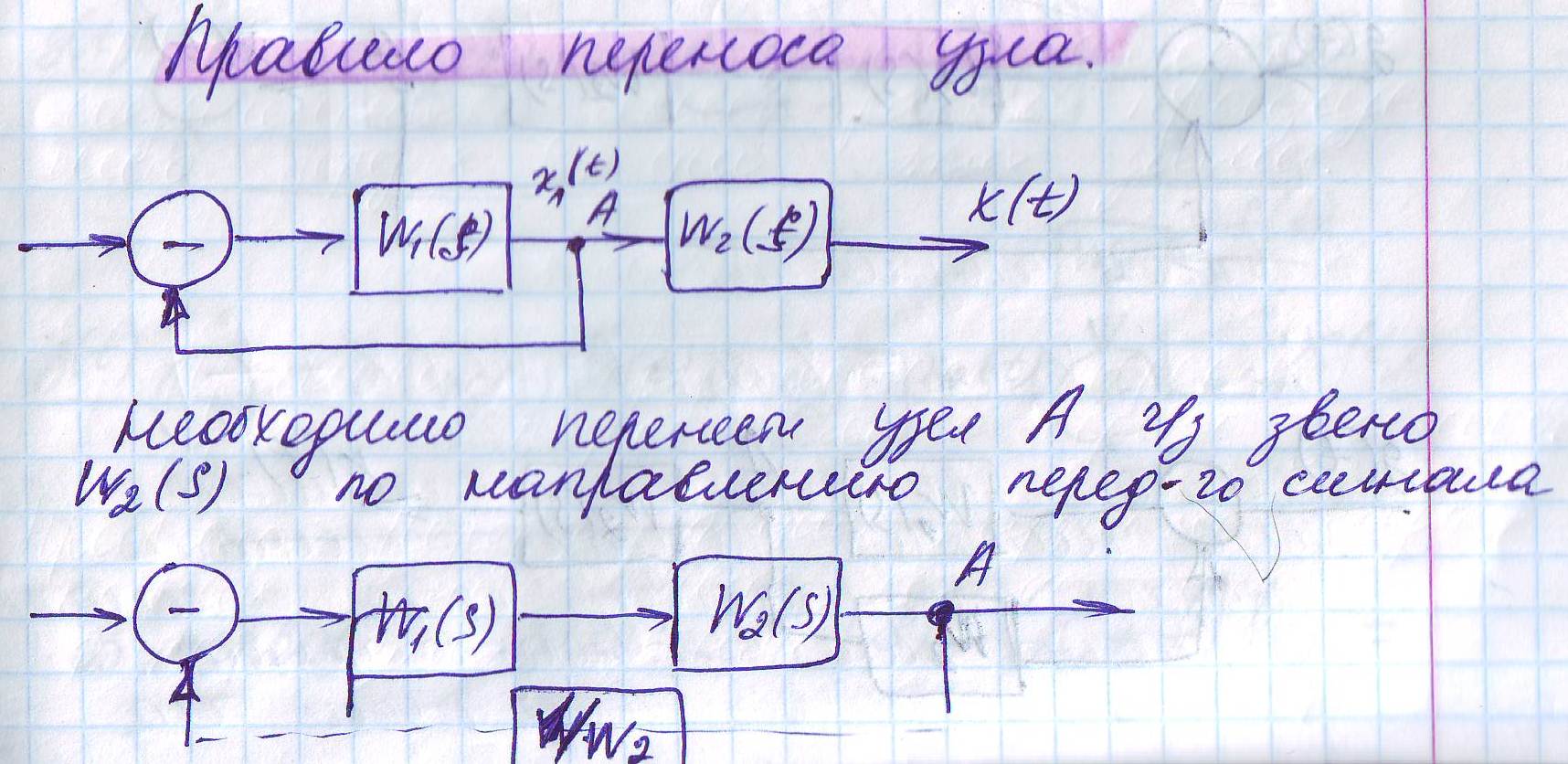
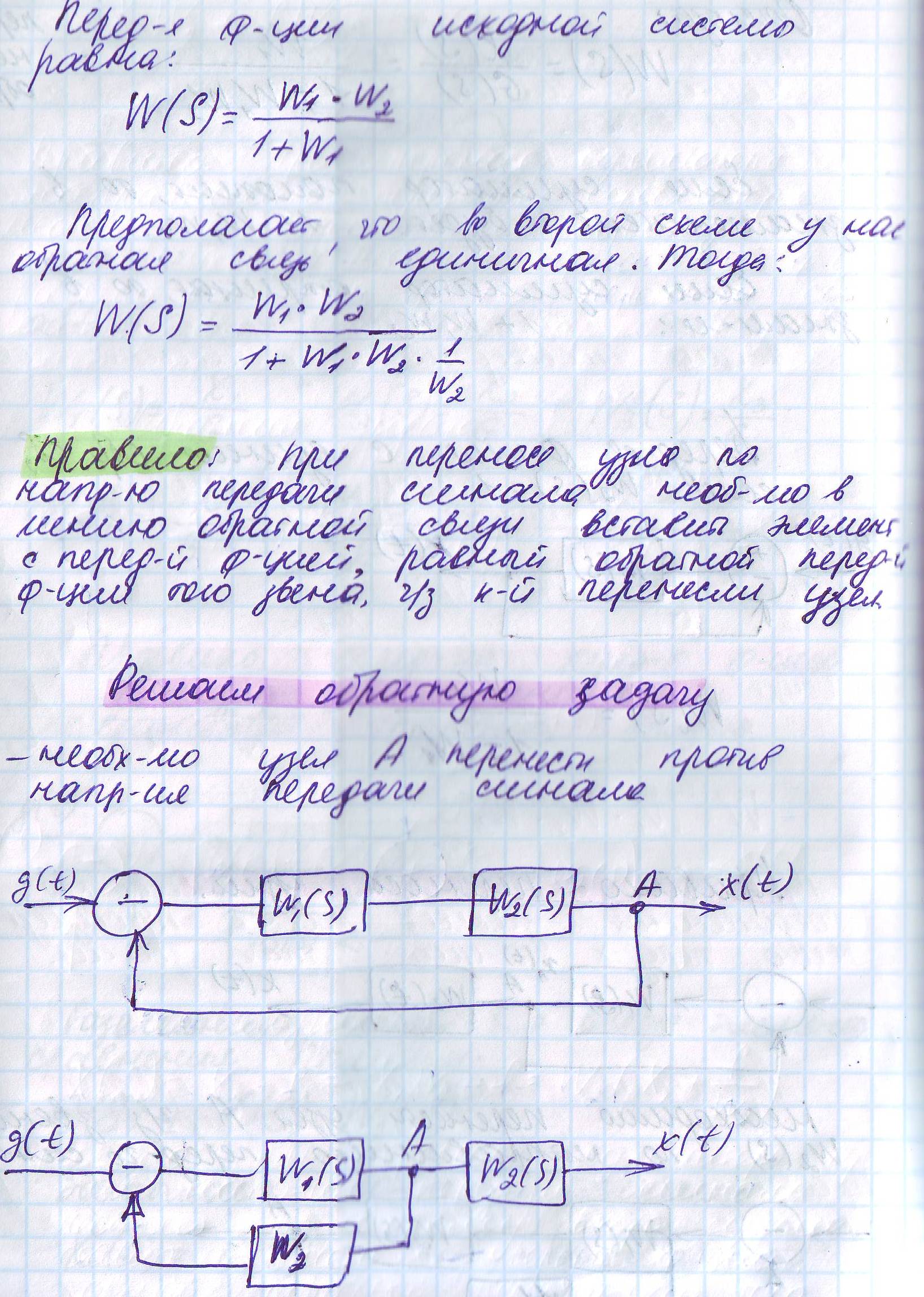
2. Типовые звенья. Дифференциальное звено 1-го порядка

Билет №18

1. Правило переноса сумматора и их перестановок

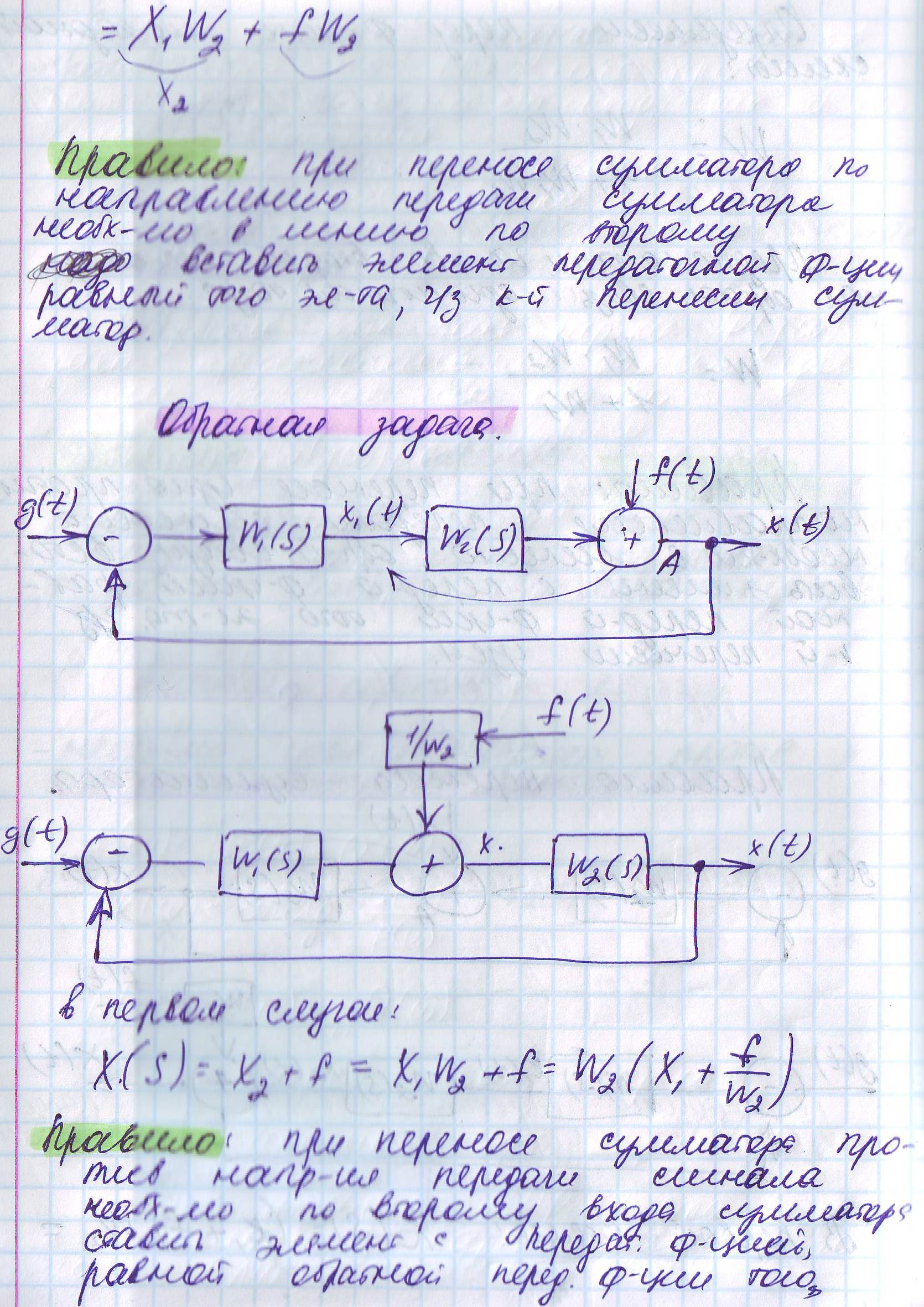
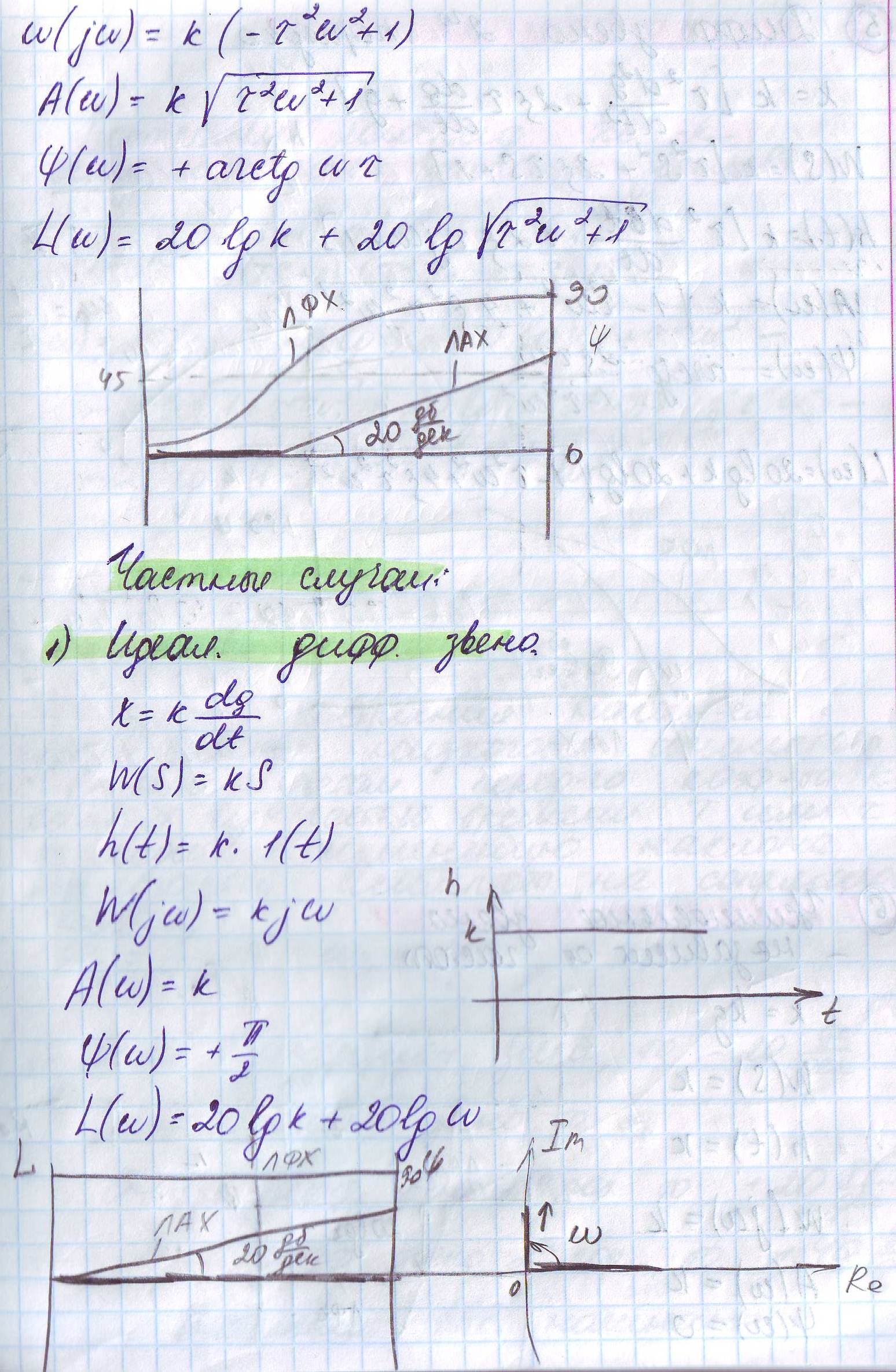
2. Типовые звенья. Колебательное звено

Билет №19

1. Характеристики динамических звеньев. Частотные характеристики

Частотные характеристики

Р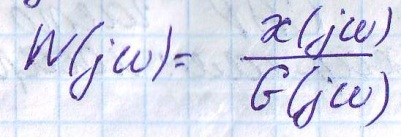 ассмотрим передаточную функцию, состоящую из n-го количества элементов.

Данное выражение показывает, как изменяется амплитуда на выходе системы при гармоническом воздействии на его вход,так же как изменяется колебания.

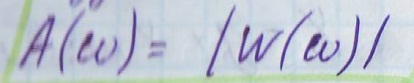
М одуль этого выражения называется ампл.-част. характеристика. дает представление о фазовом сдвиге выходных колебаний, и он называется фазово-частотной характеристикой (ФЧХ).

Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом:

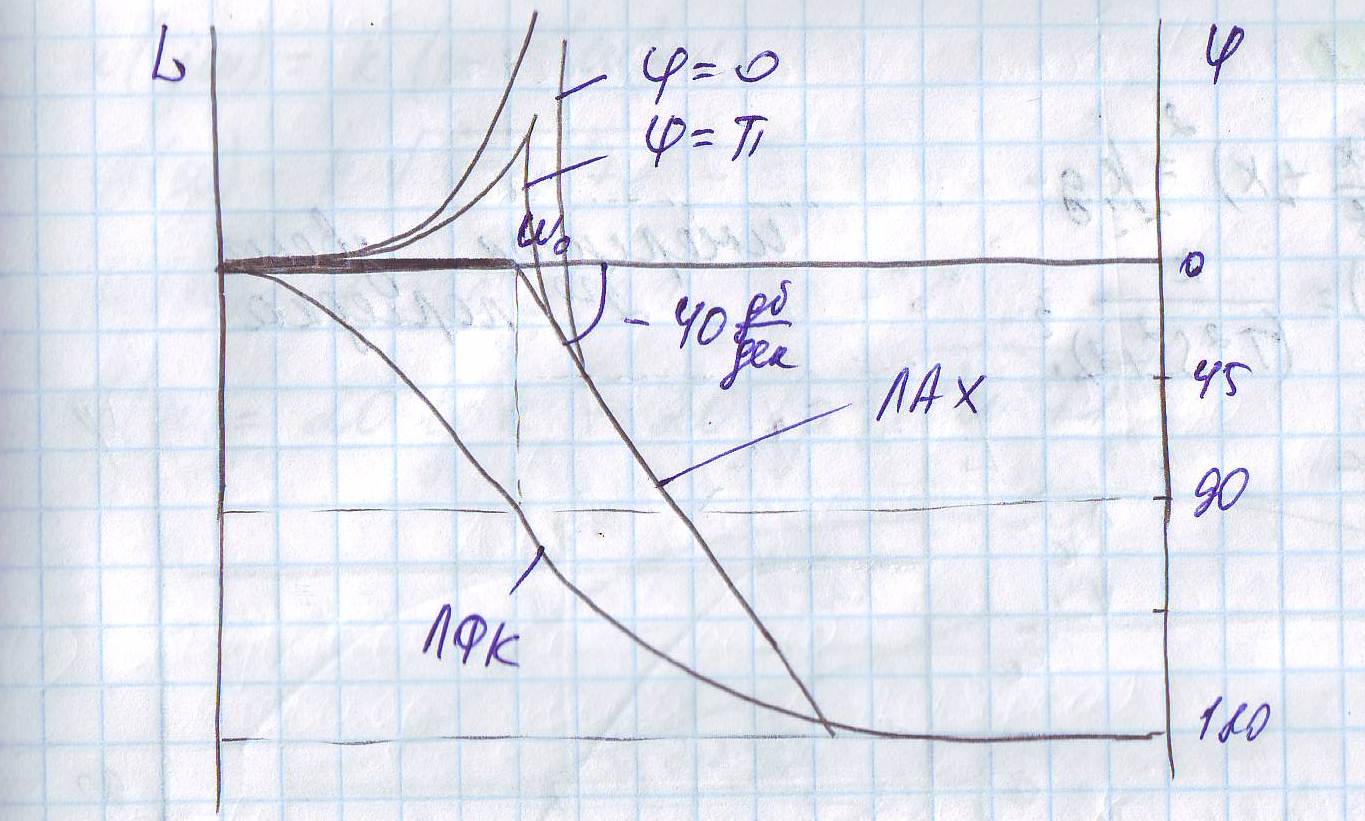
При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ

1)логариф.ампл.-част.хар-ка(ЛАХ)

2)логар.фазо-част.хар-ка(ЛФХ)

ЛАХ измер-ся усилением(децибел) L(ω) = 20lg|W(jω)| = 20lgA(ω) [дБ] .

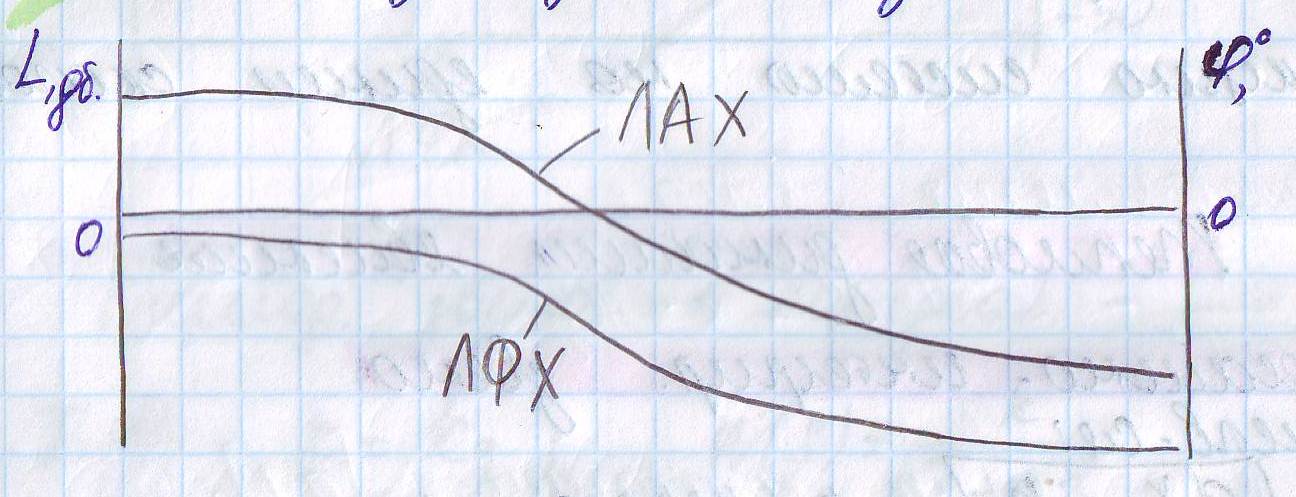Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов.