
- •Тема 1. Предмет, задачи, особенности эконометрики 7
- •Тема 2. Корреляционный и регрессионный анализ – математический метод оценки взаимосвязей экономических явлений 12
- •Введение
- •Тема 1. Предмет, задачи, особенности эконометрики
- •1.1 Cведения об истории возникновения эконометрики
- •1.2. Предмет эконометрики
- •1.3. Особенности эконометрического анализа
- •1.4. Измерения в экономике
- •Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор.
- •2.1.2. Линейная регрессия сущность, оценка параметров
- •2.1.3. Определение тесноты связи и оценка существенности уравнения регрессии
- •2.1.4 Интервальный прогноз на основе линейного уравнения регрессии
- •2.2. Нелинейная регрессия в экономике и ее линеаризация
- •2.2.1. Виды нелинейных регрессионных моделей, расчет их параметров
- •2.2.2. Оценка корреляции для нелинейной регрессии
- •2.3. Множественная регрессия и корреляция
- •2.3.1. Множественная регрессия. Отбор факторов при построении ее модели На любой экономической показатель чаще всего оказывает влияние не один, а несколько факторов.
- •2.3.2. Расчет параметров и характеристик модели множественной регрессии
- •2.3.3. Частные уравнения множественной регрессии. Индексы множественной и частной корреляции и их расчет
- •2.3.4. Обобщённый метод наименьших квадратов. Гомоскедастичность и гетероскедастичность
- •Тема 3. Информационные технологии в эконометрических исследованиях
- •Сводные экономические показатели рд за 1990-2000 гг.
- •Тема 4. Системы эконометрических уравнений
- •4.1. Понятие о системах эконометрических уравнений
- •Приравнивая это с правой частью 2-го уравнения (4.1) получаем
- •4.2. Проблема идентификации модели
- •4.3. Методы оценки параметров одновременных уравнений
- •Тема 5. Методы и модели анализа динамики экономических процессов
- •5.1. Понятие экономических рядов динамики. Сглаживание временных рядов
- •5.2. Автокорреляционная функция. Коррелограмма
- •5.3. Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •5.4. Моделирование тенденций временного ряда. Адаптивные модели прогнозирования
- •Обычно полагают
- •Тема 6. Макро- и региональные эконометрические модели
- •6.1. Макроэконометрические модели
- •Рассмотрим мультипликативную производственную функцию
- •6.2. Сущность и особенности региональных эконометрических моделей
- •6.3. Филадельфийская модель региональной экономики
- •Тема 7. Моделирование динамических процессов
- •7.1. Характеристика моделей с распределенным лагом и моделей авторегрессии
- •7.2. Выбор вида модели с распределительным лагом
- •7.3. Модели адаптивных ожиданий и неполной корректировки
- •Приложения
- •1. Базовые понятия теории вероятностей
- •1.1. Вероятность. Случайная величина
- •1.2. Числовые характеристики случайных величин
- •1.3. Законы распределений случайных величин
- •2. Базовые понятия статистики
- •2.1. Генеральная совокупность и выборка
- •2.2. Вычисление выборочных характеристик
- •3.Статистические выводы: оценки и проверка гипотез
- •4. Статистическая проверка гипотез
- •Литература
- •Эконометрике
- •Махачкала – 2008
- •Введение.
- •Лабораторная работа №1. «Корреляционный и регрессионный анализ – математический метод оценки взаимосвязей экономических явлений» Часть 1. Парная регрессия и корреляция.
- •1.1. Методические указания
- •1.2 Реализация типовых задач на компьютере.
- •Часть 2. Множественная регрессия и корреляция.
- •2.1. Методические указания
- •Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции
- •Выбор вида модели и оценка ее параметров
- •Проверка качества модели
- •Оценка влияния отдельных факторов на основе модели на зависимую переменную (коэффициенты эластичности и
- •Использование многофакторных моделей для анализа и прогнозирования развития экономических систем
- •2.2.Технология решения задач корреляционного и регрессионного анализа с помощью пакета анализа.
- •Лабораторная работа №2 «Анализ и прогнозирование временных рядов в среде Excel»
- •1. Основные понятия и определения.
- •2. Анализ временных рядов с помощью инструмента Excel-Мастер Диаграмм
Лабораторная работа №2 «Анализ и прогнозирование временных рядов в среде Excel»
1. Основные понятия и определения.
В современной экономике, в бизнесе без прогноза не обойтись. Любое серьезное решение, в особенности связанное с вложением денег требует прогноза, предвидения развития экономической ситуации.
Для того чтобы предвидеть будущее, надо хорошо знать прошлое и присущие ему закономерности.
Если в течение достаточно продолжительного времени регулярно фиксировать курсы валют, акций, цены на товары и т.д., то такие данные образуют временные ряды. Временными рядами являются также данные о выпуске или потреблении различных товаров и услуг по месяцам, кварталам, годам. В производстве временные ряды возникают при измерении количества изделий, выпускаемых подразделениями предприятия за час, смену, декаду, при оценках количества брака за те же периоды, при наблюдении за изменениями запасов на складах.
В экономике и бизнесе данные типы временных рядов появляются очень часто.
Во временном ряде содержится информация об особенностях и закономерностях протекания процесса, а статистический анализ позволяет выявить и использовать их для оценки характеристик процесса в будущем, т.е. для прогнозирования.
Временной ряд - набор чисел, привязанный к последовательным, обычно равноотстоящим моментам времени. Числа, составляющие ряд и получающиеся как результат наблюдения за ходом некоторого процесса, называются элементами, а промежуток времени между наблюдениями - шагом квантования по времени (или короче - шагом по времени). Элементы ряда нумеруют в соответствии с номером момента времени, к которому этот элемент относится (т.е. обозначают их как Y1,Y2,....,Yn).
Формально задача прогнозирования сводится к получению оценок значений ряда на некотором периоде будущего, т.е. к получению значения Yp(t), t= N + 1, N+2, .... При использовании методов экстраполяции исходят из предположения о сохранении закономерностей прошлого развития на период прогнозирования. Во многих случаях (но не всегда!) при разработке оперативного (до года) и краткосрочного (до 2 лет) прогноза эти предположения являются справедливыми.
Прогноз рассчитывается в два этапа. На первом - формальном - выявляют при помощи статистических методов закономерности прошлого развития и переносят их (экстраполируют) на некоторый период будущего. На втором - производится корректировка полученного прогноза, с учетом результатов содержательного анализа текущего состояния.
Статистические методы исследования исходят из предположения о возможности представления уровней временного ряда в виде суммы нескольких компонент, отражающих закономерность и случайность развития. в частности в виде суммы четырех компонент:
Y(t)=f(t)+S(t)+U(t)+E(t),
где f(r) - тренд (долгосрочная тенденция) развития;
S (t) - сезонная компонента;
U (t) - циклическая компонента;
Е (t) - остаточная компонента.
Сезонная компонента характеризует устойчивые внутригодичные колебания уровней, которые носят периодический или близкий к нему характер. Она проявляется в некоторых показателях, представленных квартальными или месячными данными.
В тех случаях, когда период колебаний составляет несколько лет, говорят, что во временном ряде присутствует циклическая компонента.
Основная цель статистического анализа временных рядов - изучение соотношения между закономерностью и случайностью в формировании значений уровней ряда, оценка количественной меры их влияния. Закономерности, объясняющие динамику показателя в прошлом, используются для прогнозирования его значении в будущем, а учет случайности позволяет определить вероятность отклонения от закономерного развития и его возможную величину.
При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.
Метод
отклонений от тренда
предполагает вычисление трендовых
значений для каждого временного ряда
модели, например
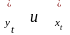 ,
и расчет отклонений от трендов:
,
и расчет отклонений от трендов:
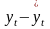 и
и
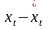 .
Для дальнейшего анализа используют не
исходные данные, а отклонения от тренда.
.
Для дальнейшего анализа используют не
исходные данные, а отклонения от тренда.
Метод последовательных разностей заключается в следующем:
Если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:
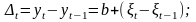
если параболический тренд – вторыми разностями:
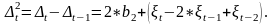
В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид
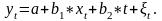
Параметры a и b в этой модели определяются обычным методом МНК.
Автокорреляция
в остатках – корреляционная
зависимость между значениями остатков
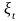 за текущий и предыдущие моменты времени.
за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина-Уотсона и расчет величины:
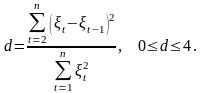
Коэффициент автокорреляции остатков первого порядка определяется по формуле
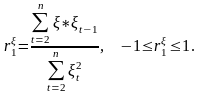
Критерий Дарбина-Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением
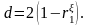
Если
в остатках существует полная положительная
автокорреляция и
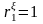 ,
то d=0.
Если в остатках полная отрицательная
автокорреляция, то
,
то d=0.
Если в остатках полная отрицательная
автокорреляция, то
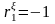 и, следовательно, d=4.
Если автокорреляция остатков отсутствует,
то
и, следовательно, d=4.
Если автокорреляция остатков отсутствует,
то
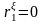 и d=2.
и d=2.
Следовательно
.
