-Система координат, связанная с ээв

Расчет полей проводится в сферической системе координат (рисунок 2).

При расчете полей вводят ограничения:

1) Излучатель находится в безграничном пространстве в идеальной среде без потерь (вакуум).

2) Длина излучателя ℓ < < l . Такое условие позволяет пренебречь запаздыванием по длине излучателя, т.е. амплитуда и фаза тока постоянны. Хотя ток переменный, на концах диполя будут скапливаться заряды.

3) Расстояния r, на которых определяется напряженность поля, много больше размеров излучателя ℓ.

4) Переменный ток в излучателе изменяется по гармоническому закону.

Решение волновых уравнений

, (1)

где - амплитуда тока.

Из трех составляющих, которые определяют rot, отличной от нуля будет только азимутальная составляющая .

^{. (2)}

Определим составляющие электрического поля, исходя из:

^{. (3)}

⁽⁴⁾

Таким образом, для элементарного электрического излучателя характерно наличие в пространстве трех составляющих Нy , Е_r, Eq (Рис.3).

Интенсивность составляющих электрических и магнитных полей зависит от угла q . Элементарный электрический излучатель, как и любой излучатель, создает в окружающем пространстве сферическую волну.

 

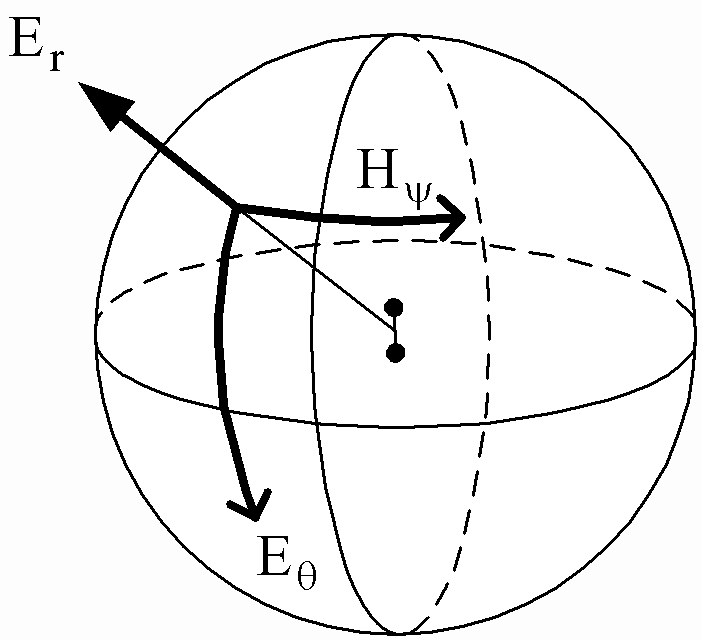
Нy - азимутальная составляющая

Е_r - радиальная составляющая

Eq - меридиональная составляющая

Рисунок 3 - Составляющие полей в пространстве элементарного

электрического излучателя

-Качественное описание излучения МВ в поперечном направлении.

Ограничимся анализом дальней зоны. Поступая так же, как и в случае элементарного электрического вибратора, получаем

Из формул (5.20) следует, что поле, создаваемое ЭМВ в дальней зоне, представляет собой неоднородную поперечную сферическую. волну, распространяющуюся от вибратора со ско­ростью света. Векторы Е и Н изменяются синфазно. На рис.5.20 показана ориентация векторов Е и Н в дальней зоне в случае ЭЭВ (рис. 5.20, а) и элементарного магнит­ного вибратора (рис. 5.20, б).

17 Напряженность электрического и магнитного полей МВ в дальней зоне. Структура электромагнитного поля МВ в дальней зоне, отличия от структуры поля ЭЭВ в дальней зоне. Волновое сопротивление среды в случае МВ. ДН МВ.

 Выражения для комплексных амплитуд составляющих век­торов поля, создаваемого элементарным магнитным вибратором, могут быть получены из формул (5.3), (5.4) и (5.5) для поля ЭЭВ, в которых нужно только в соответствии с принципом двойственности

заменить   на

(-μ) и μ на (-ε). Окончательные выражения очевидны, и мы не будем их здесь выписывать. Из формул для поля элементарного магнитного вибратора следует, что вектор Ё имеет одну составляющую  Ё_φ, а вектор  Н-две составляющие  Н_rи H_θт.е.

вектор Ё  в этом случае лежит в азимутальных плоскостях, а

вектор, Н - в меридиональных.

Как и в случае ЭЭВ, в выражениях для поля элементарного магнитного вибратора (ЭМВ) имеются слагаемые, пропорцио­нальные 1/(kr) в первой, второй и третьей степенях. Поэтому при анализе структуры поля элементарного магнитного вибратора ок­ружающее его пространство также удобно разделить на три зоны:

ближнюю (kr<<1), дальнюю (kr>>1) и промежуточную, где krсоиз­меримо с единицей.

Ограничимся анализом дальней зоны. Поступая так же, как и в случае элементарного электрического вибратора, получаем

Из формул (5.20) следует, что поле, создаваемое ЭМВ в дальней зоне, представляет собой неоднородную поперечную сферическую. волну, распространяющуюся от вибратора со ско­ростью света. Векторы Е и Н изменяются синфазно. На рис.5.20 показана ориентация векторов ЕиНв дальней зоне в случае ЭЭВ (рис. 5.20, а) и элементарного магнит­ного вибратора (рис. 5.20, б).

Распространение электромагни­тной волны сопровождается перено­сом энергии. Энергия распространя­ется со скоростью света перпендику­лярно поверхностями равных фаз, т.е. фазовая скорость и скорость распространения энергии совпадают. Отношение амплитуд напряженностей электрического и магнитного полей

Kак и элементарный электрический виоратор, элементарный магнитный вибратор обладает направленными свойствами. Его излучение максимально в экваториальной плоскости   

Вдоль своей оси (оси Z) элементарный магнитный вибратор не излучает. Диаграммы направленности элементарного магнитного вибратора совпадают с диаграммами направленности элемен­тарного электрического вибратора (рис. 5.11-5.15).

Как уже отмечалось, достаточно малая рамка (виток провода), обтекаемая постоянным по амплитуде электрическим током /_р = = /_pmcos(ωt + ψ₁), где ψ₁-начальная фаза тока, также может рассматриваться как элементарный магнитный вибратор. В этом случае вибратор характеризуется амплитудой тока (/_р) и площадью рамки S. Формулы для поля, создаваемого рамкой, могут быть получены независимо от формул для поля элементарного эле­ктрического вибратора. Для этого нужно записать выражение для

векторного потенциала кольцевого электрического тока А, вы­числить входящий в это выражение интеграл в предположении, что расстояние от рамки до точки наблюдения велико по срав­нению с размерами рамки, а затем перейти к векторам Ё и Н, как

это было сделано в случае элементарного электрического виб­ратора. Сравнение окончательных выражений для поля, соз­даваемого рамкой, с формулами для поля элементарного маг­нитного вибратора показывает, что они переходят друг в друга при замене вида

Длину ЭЭВ, при которой в случае одинаковых токов, обте­кающих рамку и вибратор  мощность излучения ЭЭВ равна мощности излучения рамки, называют действующей высотой как видно той рамки. Она равна  и из формул (5.22) и (5.6), рамка создает в дальней зоне такие же по величине (но не по ориентации векторов электрическое и магнитное поля, как и элементарный электрический вибратор.