1.Классификации сред по отношению к электромагнитному полю

Свойства среды по отношению к электромагнитному полю определяются параметрам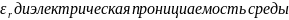

проводимость среды

Если эти параметры зависят от величины поля то линейная среда, а если хотя бы 1 параметр зависит от величины поля то среда является нелинейной.

Линейные среды делятся на 4 группы

1. Однородные, где эти параметры не зависят от координат.

2. Неоднородные, где эти параметры зависят от координат.

3. Изотропные, свойства одинаковы по всем направлениям.

4. Анизотропные, свойства различны по всем направлениям.

2.Уравнения Максвелла в дифференциальной, интегральной и комплексной формах

1 уравнение максвелла в дифференциальной форме: Электрический заряд является источником электрической индукции.

2 уравнение максвелла. Не существует магнитных зарядов

3 уравнение максвелла . Изменение магнитной индукции порождает вихревое электрическое поле

4 уравнение максвелла . Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

В том же порядке интегральная форма записи

Поток электрической индукции через замкнутую поверхность s пропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s.

Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).

Изменение потока магнитной индукции, проходящего через незамкнутую поверхность s, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре l, который является границей поверхности s.

Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность s, пропорциональны циркуляции магнитного поля на замкнутом контуре l, который является границей поверхности s.

Уравнения максвелла для комплексных амплитуд

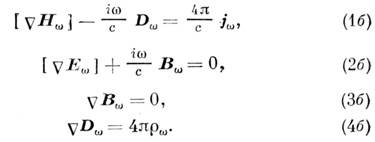
3.Уравнение баланса мгновенных значений мощности

 Как уже отмечалось в 1.1, электромагнитное поле является одной из форм материи. Как и любая другая форма материи, оно обладает энергией. Эта энергия может распространяться в про­странстве и преобразовываться в другие формы энергии.

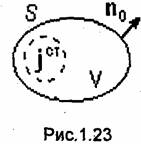
Сформулируем уравнение баланса для мгновенных значений мощности применительно к некоторому объему V, ограниченному поверхностью S (рис.1.23). Пусть в объеме V, заполненном од­нородной изотропной средой, находятся сторонние источники. Из общих физических представлений очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на джоулевы потери и на изменение энергии электромагнитного поля внутри V, а также может частично рассеиваться, уходя в ок­ружающее пространство через поверхность S. При этом должно выполняться равенство

где Р^ст-мощность сторонних источников; Р_П-мощность джоулевых потерь внутри объема V; Р_Σ -мощность, проходящая через поверхность S; W-энергия электромагнитного поля, сосредоточен­ного в объеме V, a dW/dt- мощность, расходуе­мая на изменение энергии в объеме V.

В данном разделе будут использованы уравнения состояния (1.53). Эти уравнения не позволяют учесть потери энергии при поляризации и намагничивании среды. Поэтому слагаемое Р_п в равенстве (1.120) фактически определяет мощность джоулевых потерь в объеме V, обусловленных током проводимости.

Уравнение (1.120) дает только качественное представление об энергетических соотношениях. Чтобы получить количественные соотношения, нужно воспользоваться уравнениями Максвелла. Рассмотрим первое уравнение Максвелла с учетом сторонних то­ков (1.111). Все члены этого уравнения - векторные величины, имеющие размерность А/м².

Чтобы получить уравнение, аналогичное (1.120), нужно видо­изменить первое уравнение Максвелла (1.111) так, чтобы его члены стали скалярными величинами, измеряющимися в ваттах. Для этого достаточно все члены указанного равенства скалярно умножить на вектор Е, а затем проинтегрировать полученное выражение по объему V. После скалярного умножения на вектор Е получаем

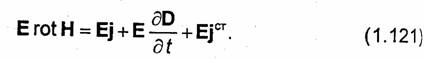
Используя известную из векторного анализа формулу div[E,H]= = Н rot Е - Е rot H, преобразуем левую часть соотношения (1.121) и заменим rot E его значением из второго уравнения Максвелла (1.39):

Подставляя это выражение в (1.121), получаем

В последнем слагаемом в правой части (1.122) изменен порядок сомножителей в скалярном произведении векторов dB/dt и Н. Это допустимо, так как Н dB/dt = дВ/дt· H. Данное изменение не яв­ляется принципиальным и не дает никаких преимуществ при выводе рассматриваемого здесь уравнения баланса для мгно­венных значений мощности. Однако при такой записи во всех членах уравнения (1.122) второй сомножитель (векторы j^ст, j, BDIdt и Н) является вектором, входившим ранее в первое уравнение Максвелла. Это обстоятельство позволит в дальнейшем (см. 1.8.4) несколько упростить вывод уравнения баланса в случае моно­хроматического поля (уравнения баланса комплексной мощности). Интегрируя почленно уравнение (1.122) по объему V, получаем

где направление элемента dS совпадает с направлением внешней нормали к поверхности S. При переходе от.(1.122) к (1.123) ис­пользована теорема Остроградского-Гаусса для перевода объем­ного интеграла от div[E, H] в поверхностный интеграл от вектор­ного произведения [Е, Н]. Введем обозначение

и    преобразуем    подынтегральное   выражение   в   последнем слагаемом в правой части (1.123):

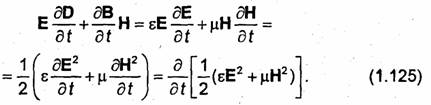
Подставляя (1.124) и (1.125) в (1.123) и меняя порядок интег­рирования и дифференцирования, получаем

Выясним физический смысл выражений, входящих в уравнение (1.126).

Рассмотрим первое слагаемое в правой части (1.126). Пред­ставим объем V в виде суммы бесконечно малых цилиндров длиной dl, торцы которых (dS) перпендикулярны направлению тока (вектору j). Тогда EjdV = EjdV=(Edl)(jdS) = dUdl = dP_n, где dl  =jdS - ток, протекающий по рассматриваемому бесконечно мало­му цилиндру; dU = Edl - изменение потенциала на длине dl, a dP_n -мощность джоулевых потерь в объеме dV. Следовательно, рас­сматриваемое слагаемое представляет собой мощность джоу­левых потерь Р_п в объеме V. Используя соотношение j = σЕ, для Р_п можно получить и другие представления:

Формулы (1.127) можно рассматривать как обобщенный закон Джоуля-Ленца, справедливый для проводящего объема V произ­вольной формы.

Интеграл в левой части (1.126) отличается от первого сла­гаемого в правой части только тем, что в подынтегральное выражение вместо j входит j^cт. Поэтому он должен определять мощность сторонних источников. Будем считать положительной мощность, отдаваемую сторонними токами электромагнитному по­лю. Электрический ток представляет собой упорядоченное дви­жение заряженных частиц. Положительным направлением тока считается направление движения положительных зарядов. Ток отдает энергию электромагнитному полю при торможении обра­зующих его заряженных частиц. Для этого необходимо, чтобы вектор напряженности электрического поля Е имел составляющую, ориентированную противоположно направлению тока, т.е. чтобы скалярное произведение векторов Е и j^ст было отрицательным (E j^ст <0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, определяется выражением

Для уяснения физического смысла последнего слагаемого в правой части уравнения (1.126) рассмотрим частный случай. Предположим, что объем V окружен идеально проводящей обо­лочкой, совпадающей с поверхностью S. Тогда касательная сос­тавляющая вектора Е на поверхности S будет равна нулю. Эле­мент поверхности dS совпадает по направлению с внешней нор­малью n₀. Следовательно, поверхностный интеграл в уравнении (1.126) будет равен нулю, так как нормальная компонента век­торного произведения [Е, Н] определяется касательными состав­ляющими входящих в него Векторов. Кроме того, предположим, что среда в пределах объема V не обладает проводимостью ( σ = 0). При этом в рассматриваемой области не будет джоулевых потерь, и первый интеграл в правой части уравнения (1.126) также будет равен нулю. В результате получим

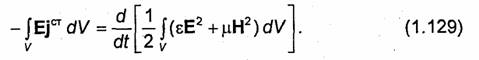
Очевидно, что в рассматриваемом случае мощность сто­ронних источников может расходоваться только на изменение энергии электромагнитного поля. Таким образом, правая часть равенства (1.129) представляет собой скорость изменения энергии электромагнитного поля, запасенной в объеме V, т.е. соответ­ствует слагаемому dW/dt в уравнении (1.126). Естественно пред­положить, что интеграл в правой части (1.129) равен энергии электромагнитного поля, сосредоточенного в объеме V:

Строго говоря, этот интеграл может отличаться от W на не­которую функцию g = g(х, у, z), не зависящую от времени. Не­трудно убедиться, что функция д равна нулю. Перепишем (1.130) в виде W=W^Э+W^М, где

Предположим, что электрическое и магнитное поля являются постоянными (не зависят от времени). В этом случае, как известно из курса физики (см. также гл.З и 4), выражения (1.131) и (1.132) определяют энергию соответственно электрического и магнитного полей в объеме V. Но это означает, что g = 0 и указанные вы­ражения определяют мгновенные значения энергии электричес­кого и магнитного полей в объеме V при любой зависимости от временила их сумма, определяемая формулой (1.130), дейст­вительно равна мгновенному значению энергии электромагнитного поля в объеме V.

Осталось выяснить физическую сущность поверхностного ин­теграла в уравнении (1.126). Предположим, что в объеме V от­сутствуют потери и, кроме того, величина электромагнитной энер­гии остается постоянной (W= const). При этом уравнение (1.126) принимает вид

В то же время из физических представлений очевидно, что в данном частном случае вся мощность сторонних источников должна уходить в окружающее пространство (Р^ст = Р_Σ). Следо­вательно, правая часть уравнения (1.133) равна потоку энергии через поверхность S (пределу отношения количества энергии, проходящей через S за время Δt при Δt→0), т.е.

Естественно предположить, что вектор П представляет собой плотность потока энергии (предел отношения потока энергии через площадку ΔS, расположенную перпендикулярно направлению ра­спространения энергии, к ΔS  при ΔS →0). Формально матема­тически это предположение не очевидно, так как замена вектора П на П₁ = П + rot а, где а - произвольный вектор, не изменяет ве­личину Р_Σ. Однако оно является верным и в частности, непо­средственно вытекает из релятивистской теории электромаг­нитного поля [11].

Таким образом, равенство (1.126) аналогично (1.120) и пред­ставляет собой уравнение баланса мгновенных значений мощ­ности электромагнитного поля. Оно было получено Пойнтингом в 1884 г. и называется теоремой Пойнтинга. Соответственно век­тор П называют вектором Пойнтинга. Часто используют также названия "теорема Умова-Пойнтинга" и "вектор Умова-Пойн-тинга" с целью подчеркнуть тот факт, что формулировка закона сохранения энергии в общей форме с введением понятия потока энергии и вектора, характеризующего его плотность, впервые была дана Н.А. Умовым в 1874 г.

Отметим, что энергия может поступать в объем V не только от сторонних источников. Например, поток энергии через поверхность S может быть направлен из окружающего пространства в объем V. При этом мощность P_Σ будет отрицательной, так как положи­тельным считается поток энергии, выходящий из объема V в окружающее пространство (направление элемента dS совпадает с направлением внешней нормали к поверхности S).

Сторонние источники могут не только отдавать энергию, но и получать ее от электромагнитного поля. При этом мощность сто­ронних источников будет отрицательной. Действительно, элект­ромагнитное поле отдает энергию току проводимости, если оно ускоряет движение заряженных частиц, образующих ток. Для этого вектор напряженности электрического поля Е должен иметь сос­тавляющую, ориентированную вдоль линий тока, т.е. чтобы ска­лярное произведение векторов Е и j^ст было больше нуля.

Рассмотрим более подробно формулы, определяющие энер­гию   электромагнитного   поля.   Подынтегральные   выражения   в

можно интерпретировать как мгновенные значения объемных плотностей энергии элект­рического и магнитного полей соответственно, а их сумму

- как объемную плотность полной энергии электромагнитного поля.

Подчеркнем, что принцип суперпозиции, которому удовле­творяют векторы напряженностей электрического и магнитного полей, не распространяется на энергию. Действительно, пусть энергии полей E₁, H₁ и Е₂, Н₂, существующих по отдельности в области V, равны соответственно W₁ и W₂. Тогда энергия сум­марного поля Е = Е₁ + Е₂, Н = Н₁ + Н₂ определится выражением

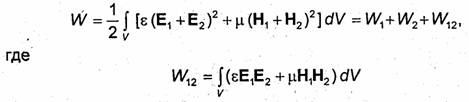
- взаимная энергия полей. Взаимная энергия W₁₂ может быть как положительной, так и отрицательной. Если векторы Е₁ и Е₂, а также H₁ и Н₂ взаимно перпендикулярны, то W₁₂ = 0.

В случае переменных процессов распределение электро­магнитной энергии непрерывно изменяется. Это изменение в каждой данной точке можно определить на основе уравнения (1.122), которое удобно представить в виде

где p^ст =-E j^ст и p_n = Ej-мгновенные значения плотностей мощности сторонних источников и мощности джоулевых потерь соответственно. При переходе от соотношения (1.122) к уравнению (1.136) учтены формулы (1.125) и (1.135). Уравнение (1.136) является дифференциальной формой теоремы Пойнтинга.