Наблюдатель Калмана - Бьюси
Рассмотрим следующую задачу оптимального оценивания (наблюдения). Пусть объект и наблюдение описываются уравнениями:
,
,
(8.21)
,
(8.22)
где
- гауссовские белые шумы с характеристиками
;
,
;
,
,
- гауссовская случайная величина с характеристиками
;
,
– неотрицательно-определенные
симметричные матрицы (
;
);
– положительно-определенная симметричная
матрица (
).
Случайные процессы
и
называются соответственно шумом объекта
и шумом наблюдения или измерения. Они
не коррелированны со случайной величиной
.
Требуется, используя
измеренные значения выходной переменной
на интервале
,
найти несмещенную оценку
,
обеспечивающую минимум среднего квадрата
ошибки:
. (8.23)
Условие
означает, что ни одна компонента выходной
координаты
не измеряется точно. В этом случае задача
оценивания называется несингулярной.
Несмещенная
оптимальная оценка
определяется из уравнения
;
, (8.24)
где матрица коэффициентов усиления
; (8.25)
- дисперсионная
матрица ошибки
,
которая и находится из дисперсионного
уравнения
;
;
.
(8.26)
Если шумы объекта
и наблюдения не коррелированны
,
то из (8.25), (8.26) следует:
;
; (8.27)
; .
Несингулярная задача оценивания при некоррелированных шумах впервые была решена Р.Калманом и Бьюси. Ее решение представляет собой оптимальный наблюдатель и называется наблюдателем (оценивателем) или чаще фильтром Калмана - Бьюси.
Сравнивая уравнение
объекта (8.21) и оптимального наблюдателя
(8.24), замечаем, что их правые части
отличаются только последними слагаемыми:
в уравнении наблюдателя вместо шума
объекта появляется слагаемое,
пропорциональное разности
.
Эта разность между измеренным текущим значением выходной координаты и ее оценкой называется невязкой.
Структурная схема наблюдателя Калмана-Бьюси включает в себя как составную часть модель исходной системы с измерителем. Ее отличие от заданной системы состоит в том, что она имеет дополнительную обратную связь по невязке (рис. 8.1).
Наблюдатель Калмана-Бьюси имеет такую же структуру, что и наблюдатель полного порядка в детерминированном случае.
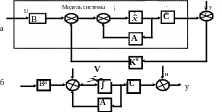
Рис.8.1. Структурная схема наблюдателя Калмана-Бьюси –а
и модель исходной системы – б
Соотношения (8.24) - (8.27) определяют также решение задачи линейного оптимального оценивания, которая отличается от задачи оптимального оценивания (8.21) - (8.23) тем, что:
1) о законах распределения шумов и начального состояния никаких предположений не делается (не требуется, чтобы они были гауссовскими);
2) нужно найти оптимальный наблюдатель в классе линейных систем, т.е. если шумы и начальное состояние не являются гауссовскими, то наблюдатель Калмана-Бьюси является оптимальным только среди линейных наблюдателей (систем).
Наблюдатель при цветном шуме объекта
В случае, если шум объекта является цветным, уравнения (8.21), (8.22) представляют в виде
;
,
где
- белый шум с характеристиками
- случайный вектор
с характеристиками
;
- шум объекта.
Предполагается, что шум объекта является цветным и удовлетворяет уравнению
,
где
- белый шум с характеристиками
- случайный вектор
с характеристиками
.
Дифференциальное уравнение для называется уравнением формирователя (формирующего фильтра) или формирователем, он формирует из белого шума с известными характеристиками заданный цветной шум.
Введем обозначения
;
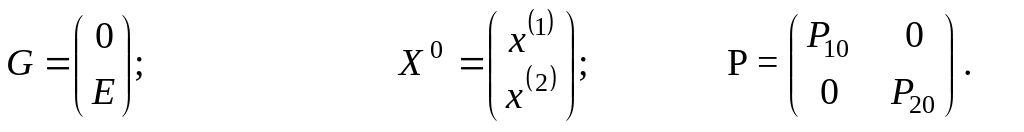
Тогда приведенные уравнения можно представить в виде
,
.
Шум объекта есть
с интенсивностью
,
поэтому наблюдатель Калмана-Бьюси при
цветном шуме объекта описывается теми
же уравнениями (8.24) – (8.27), но при условии,
что в дисперсионном уравнении вместо
подставляется
.
При некоррелированных шумах
и
имеем:
;
.
Представим дисперсионную матрицу в виде блоков
.
Тогда матрицу
и уравнение для оценки представим
следующим образом
Из матричного
уравнения для
можно получить уравнения для
и
.
Наблюдатель Калмана-Бьюси при цветном шуме объекта помимо модели исходной системы включает еще модель формирователя (рис. 8.2).
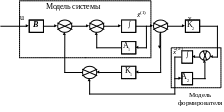
Рис. 8.2. Структурная схема оптимальной системы при цветном шуме объекта