
- •7.5. Основные результаты раздела
- •8. Стохастические оптимальные системы
- •8.1. Метод динамического программирования
- •Достаточное условие оптимальности.
- •8.2. Синтез оптимальной системы при полной информации о состоянии
- •8.3. Синтез оптимальных систем управления при неполной информации
- •Наблюдатель Калмана - Бьюси
- •Наблюдатель при цветном шуме объекта
- •Наблюдатель при цветном шуме наблюдения
- •8.4. Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- •8.5. Основные результаты раздела
- •9. Оптимальные дискретные системы
- •9.1. Синтез оптимальной линейной системы при квадратичном критерии
- •9.2. Стохастическая оптимальная линейная система при полной информации о состоянии
- •9.3. Наблюдатель (фильтр) Калмана
- •9.4. Стохастическая система управления при неполной информации
- •Приложение 1 п1. Функционал и его экстремумы
- •Приложение 2 п2. Матрицы. Дополнительные сведения
- •Характеристическая матрица, характеристические уравнения и собственные значения
где движение
происходит по окружности с линейной
скоростью R по часовой
стрелке. При
![]() система уравнений динамики объектов
имеет вид:
система уравнений динамики объектов
имеет вид:
![]()
а фазовые траектории описываются уравнением
![]()
и
представляют собой окружности с центром
в точке (1,0). При
![]() система уравнений объекта имеет вид:
система уравнений объекта имеет вид:
![]()
а фазовые траектории удовлетворяют уравнению окружностей с центром в точке (-1,0):
![]() .
.
Семейства фазовых траекторий системы для и приведены на рис. 7.10.


Рис. 7.10. Семейства фазовых траекторий системы
для случаев и
Из рис. 7.10 видно,
что начала координат система может
достичь только с одной из траекторий с
радиусом
![]() (они
выделены и проходят через начало
координат), но на эти траектории необходимо
попасть. Как это происходит, оценим по
рис. 7.11. Пусть на последнем участке
угловой длиной
(они
выделены и проходят через начало
координат), но на эти траектории необходимо
попасть. Как это происходит, оценим по
рис. 7.11. Пусть на последнем участке
угловой длиной
![]() у нас управление
(см. рис 7.10), то есть мы проходим (рис.
7.11) последний этап управления по
окружности с
из (1,0) с центральным углом
.
Предпоследний этап (длиной
у нас управление
(см. рис 7.10), то есть мы проходим (рис.
7.11) последний этап управления по
окружности с
из (1,0) с центральным углом
.
Предпоследний этап (длиной
![]() )
представляет собой дугу полуокружности
)
представляет собой дугу полуокружности
![]() с центром в (-1,0) и управлением
.
В точке В необходимо произвести
переключение на
и на дуге
с центром в (-1,0) и управлением
.
В точке В необходимо произвести
переключение на
и на дуге
![]() длиной
использовать
только его. На первом этапе (дуга
длиной
использовать
только его. На первом этапе (дуга
![]() )
мы используем
.
Центральный угол
)
мы используем
.
Центральный угол
![]() равен
равен
![]() .
.
Таким образом, находясь в точке D и двигаясь по траектории DCBAO, используем управление , если находимся ниже линии, указанной пунктиром, и , если выше нее. На пунктирной линии мы производим переключение управления на противоположное. И так до тех пор, пока мы не окажемся в начале координат по траектории DCBAO. Линия переключения, которая состоит из цепочки полуокружностей, может быть представлена уравнением
![]()
что
представляет собой слева от оси
![]() верхние полуокружности, а справа –
нижние.
верхние полуокружности, а справа –
нижние.

Рис.
7.11. Траектория системы для
![]() из
рис. 7.9.
из
рис. 7.9.
7.5. Основные результаты раздела
Для линейно-квадратической нестационарной задачи синтеза оптимального управления
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
детерминированная заданная функция,
оптимальное управление равно:
-
детерминированная заданная функция,
оптимальное управление равно:
![]() ,
,
где
симметричная матрица
![]() положительно определена и отыскивается
вместе с вектором
положительно определена и отыскивается
вместе с вектором
![]() из уравнения:
из уравнения:
![]() ,
,
![]() ,
,
это так называемое дифференциальное матричное уравнение Риккати, и из уравнения
![]() ,
,
![]() .
.
Если
![]() ,
то
,
то
![]() ,
,
а
функция
![]() .
.
Для стационарной
системы, у которой A, B, Q,
R постоянны и
![]() матрица
матрица
![]() постоянная и определяется из алгебраического
матричного уравнения Риккати
постоянная и определяется из алгебраического
матричного уравнения Риккати
![]() ,
,
а оптимальное управление равно
![]() .
.
Для управления системы по выходу, то есть
![]() ,
,
,
,
,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
функционал
с помощью замены
![]() приведём к виду
приведём к виду
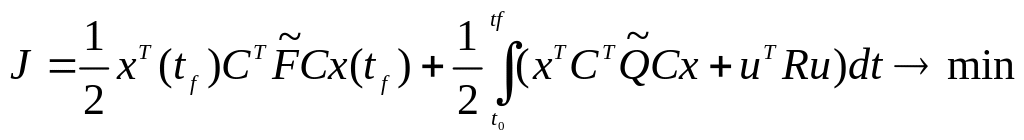 ,
,
и
оптимальное управление существует,
если
![]() ,
,
![]() ,
и определяется из предыдущей задачи с
заменой
,
и определяется из предыдущей задачи с
заменой
![]() ,
,
![]() .
.
Для линейных систем с ограничением на управление в виде неравенств в задачах максимального быстродействия
![]() ,
,
,
,
,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
синтез проводится на основании построения линий (поверхностей) переключения.
Оптимальное управление равно
![]() ,
,
причём
![]() ,
,
где
![]() ,
,
![]() .
.
Моменты переключения определяются из уравнения
![]() ,
,
и с его же помощью пытаются построить линию (поверхность) переключения.
ЗАДАЧИ
Сформулируйте общую постановку задачи синтеза оптимального управления.
Как вы думаете, почему для синтеза оптимального управления в рассмотренных задачах используется метод динамического программирования?
Какие соотношения элементов матриц
 ,
,
 и
и
 вы предложите, если для вас существенным
фактором является:
вы предложите, если для вас существенным
фактором является:
а) величина энергетических затрат;
б) близость к программной траектории в процессе функционирования системы;
в) точность достижения системой конечного состояния.
Что представляет собой регулятор выхода?
Синтезировать управление системой, динамика которой описывается системой
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
 .
.
Для
можно решить уравнение Риккати и получить
два значения
![]() .
Как определить, каким из них следует
воспользоваться?
.
Как определить, каким из них следует
воспользоваться?
В задаче 5 положить
 и
и
 .
Определить для этого случая зависимость
уравнения от
.
Определить для этого случая зависимость
уравнения от
 и
и
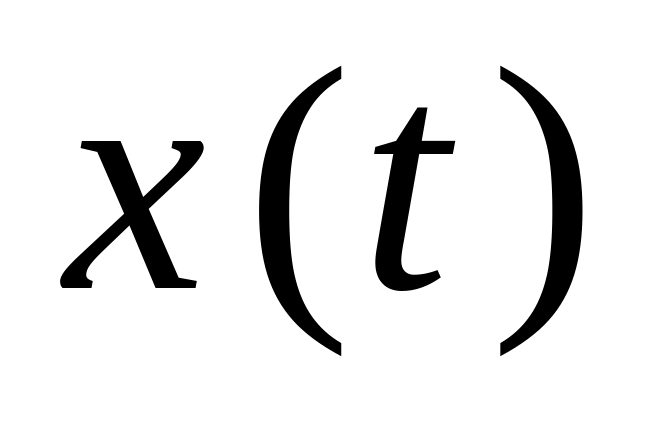 .
.В задаче 5 приравнять
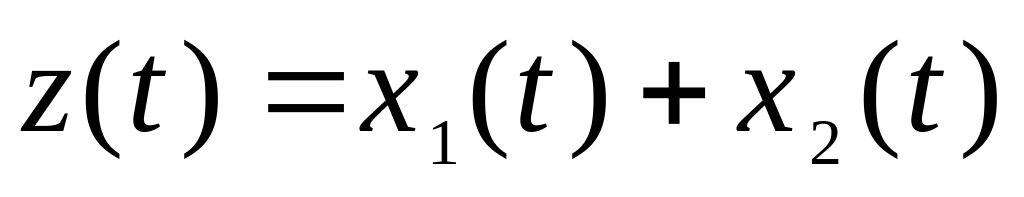 .
Определить управление,
минимизирующее функционал
.
Определить управление,
минимизирующее функционал
 .
.Выполнить синтез управления для системы из задачи 5 с
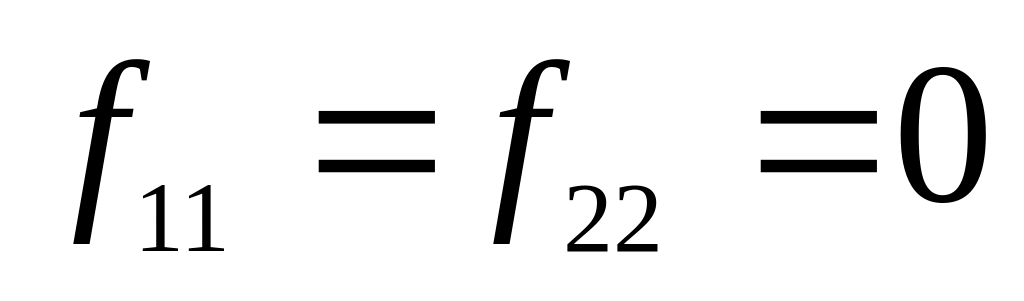 ,
,
 ,
,
 ,
.
,
.Синтезировать управление для системы
 ,
с условием минимизации критерия
,
с условием минимизации критерия
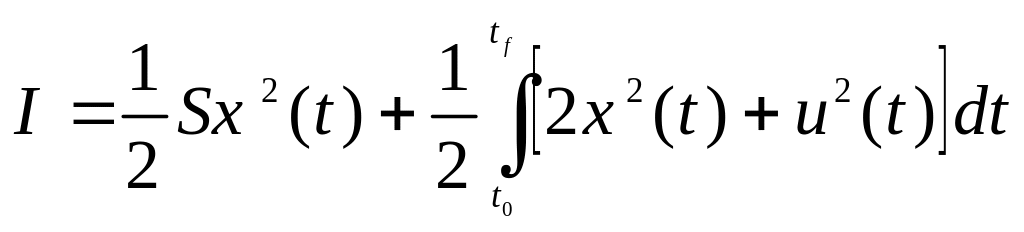 .
Рассмотреть случаи:
.
Рассмотреть случаи:
 ,
,
 и
и
 .
.Определить поверхность переключения для управления с минимальным временем, которое переводит систему
 ,
,
 ,
,
 в начало координат.
в начало координат.Определить поверхности переключения для управления с минимальным временем, которое переводит систему
 ,
,
 ,
в начало координат.
,
в начало координат.Показать, что задачи 3 и 4 связаны линейным преобразованием
 .
Как такое преобразование влияет на
поверхности переключения в этих двух
задачах?
.
Как такое преобразование влияет на
поверхности переключения в этих двух
задачах?Определить поверхность переключения для управления с минимальным временем, которое переводит систему
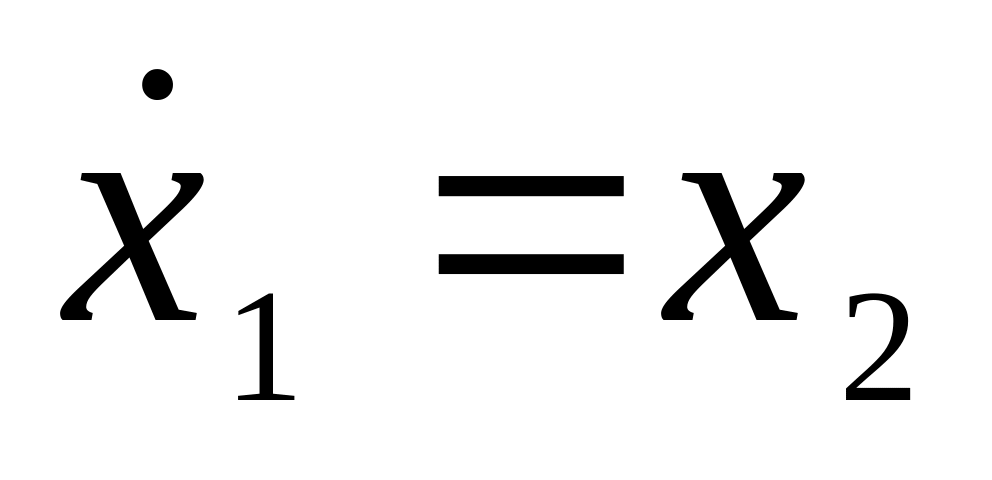 ,
,
 ,
,
 ,
,
в начало координат.
,
,
в начало координат.Выполнить синтез управления для системы
![]() ,
,
![]() ,
,
![]() ,
,
с минимизируемым функционалом вида
![]() ,
,
где
![]() - некоторая заданная функция, которую
можно положить: а) константой; б)
- некоторая заданная функция, которую
можно положить: а) константой; б)
![]() .
В условии положить вначале, что
конечно, а затем
.
.
В условии положить вначале, что
конечно, а затем
.
Выполнить синтез управления в задаче максимального быстродействия в системе:
,
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Проанализировать зависимость линии переключения от структуры матрицы А (вернее, от собственных значений матрицы).
Выполнить синтез управления в задаче максимального быстродействия для системы:
,
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Найти уравнение линии переключения и построить её график.
Выполнить синтез управления в задаче максимального быстродействия для системы:
,
![]() ,
,
,
.
,
,
,
.
Найти уравнение линии переключения и построить её график.
Выполнить синтез управления и исследовать его характер для системы:
![]() ,
,
![]() ,
,
![]() ,
,
,
,
где минимизируемый функционал имеет вид:
![]() .
.
