12. Определение параболы. Доказать ее свойства.

Параболой называется линия на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой её уравнение примет вид .

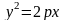Величину 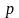называют фокальным параметром параболы, точку 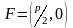– фокусом, ось – фокальной осью, прямую 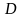: 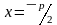– директрисой.

Свойства параболы

1. Фокальное свойство: отсутствует.

2. Директориальное свойство: парабола – ГМТ (геометрическое место точек), равноудаленных от фокуса и директрисы, т.е. .

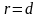Доказательство:

Рассмотрим , . Тогда , , . ■

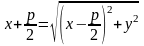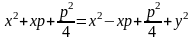3. Оптическое свойство: парабола – ГМТ (геометрическое место точек), в которых касательная образует равные углы с фокальным радиусом 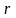и положительным направлением оси .

Д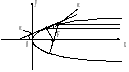 ругими словами, лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы, образуют пучок, параллельный оси параболы. И наоборот, все лучи, параллельные фокальной оси, отражаясь от параболы, попадают в фокус параболы.

Доказательство:

Р ассмотрим параболу или 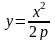. Покажем, что .

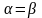Запишем уравнение касательной к параболе, проходящей через точку : .

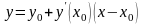1. рис.2.56

Так как 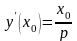, то

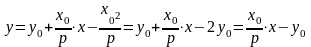. По директориальному свойству 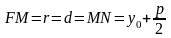. Отсюда 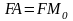. Следовательно, треугольник равнобедренный, т.е. . ■

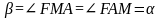13. Повехности второго порядка. Полчить уравнения цилиндрических поверхностей и поверхностей вращения.

Если у поверхности вращения заменить , т.е. сжать все эти поверхности вдоль оси , то получаются общие поверхности второго порядка. Исследовать их легко с помощью метода сечений (некоторые поверхности второго порядка не являются поверхностями вращения).

рис.2.58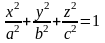

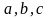1. Эллипсоид: , – полуоси эллипсоида. Из у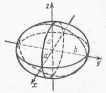 равнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида. Пересечём поверхность плоскостью 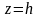, параллельной плоскости . Тогда уравнение линии, полученной в сечении, имеет вид

.

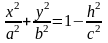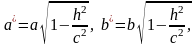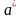Полагая получим уравнение эллипса с полуосями и .

Аналогичная ситуация возникает при пересечении эллипсоида плоскостями, параллельными плоскост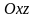ям и . Заметим, что эллипсоид с равными полуосями: 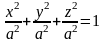называют сферой.

Из уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида.

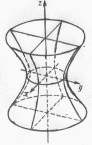
2. Однополостной гиперболоид.

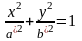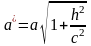
Из уравнения следует, что координатные плоскости являются плоскостями симметрии однополостного гиперболоида. Пересечение поверхности плоскостью есть эллипс: , где , . Сечения однополосного гиперболоида координатными плоскостями и 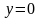представляют собой гиперболы, определяемые уравнениями соответственно

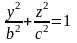14. и .

3. Двуполостной гиперболоид:

15. .

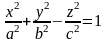Из уравнения видно, что координатные плоскости являются плоскостями симметрии, а начало координат центром симметрии двух полосного гиперболоида.

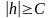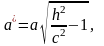
Сечение поверхности плоскостью (при ) представляет собой эллипс с полуосями 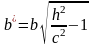. Сечения двуполостного гиперболоида плоскостями и представляют собой гиперболы

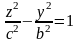
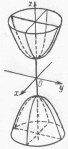и соответственно.

4. Эллиптический параболоид: .

З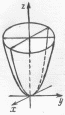 аметим, что координатные плоскости и являются плоскостями симметрии эллиптического параболоида. Ось 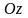называют осью данной поверхности. Сечение поверхности плоскостью , представляет собой эллипс , где .

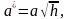
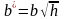Сечения эллиптического параболоида плоскостями и являются параболам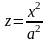и и .

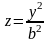5. Конус: .

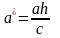Отметим, что координатные плоскости являются плоскостями симметрии, я начало координат – центром симметрии конуса. Сечение к онуса плоскостью представляет собой эллипс: с полуосями и .

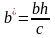При пересечении конуса плоскостями и получаются пары пересекающихся прямых

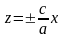и , соответственно, проходящих через начало