UML_4822 дм практикум

ских процессов главной научной и прикладной проблемой становится работа не только с существующими моделями, но и создание новых более адекватных отображаемым процессам моделей. Вчера это была логика цифровых схем сетевого планирования, сегодня – это проектирование системных моделей, применение формальных грамматик в объектноориентированном программировании, конструирование моделей в базисе нечеткой, порядковой логики. В такой ситуации инструментарий дискретной математики нужен не как метод расчета, а как метод мышления, как язык, как средство формулирования и организации понятий.

Нам очень хотелось, чтобы учебное пособие приблизило будущего специалиста именно к такой математике. В книге можно выделить следующие разделы: теории множеств, комбинаторика, исчисление высказываний, алгебра логики, приложения алгебры логики, логика предикатов. В конце пособия приведен список литературных источников, который позволит читателю получить более глубокий взгляд на прикладную значимость дискретной математики для решения задач по синтезу моделей радиотехнических и телекоммуникационных систем и сетей.

И, наконец, несколько слов о построении пособия. Значительная часть его может рассматриваться как «специальный тренинг на дому». Хорошо известно, что одним из лучших способов усвоения разделов математики является решение циклов задач без преподавателя. Его роль заменяет описание постановки «условия задачи, пояснение по его решению». По мнению авторов пособия, труд, потраченный на размышление над решением задачи, не окажется напрасным. Если же читатель нашел решение самостоятельно, ему следует просмотреть указания и решения, так как в них может содержаться дополнительная информация. В то же время мы, конечно, не хотим навязывать этот вариант решения и искренне желаем читателю творческого восприятия материала.

5

1.Теория множеств

1.1.Понятие множества. Элементы. Способы задания

множеств

Приводимые здесь определения, понятия и теоремы изложены с позиций так называемой наивной теории множеств. Известны и другие построения теории множеств, например, конструктивное и формалистское, в которых понятие множества вводится по-иному (в конструктивной теории множеств понятие множества является определяемым). С позиции наивной теории множеств понятие множества является первоначальным, неопределяемым.

Под множеством понимают любую совокупность определенных и отличных друг от друга объектов нашей интуиции или интеллекта, мыслимое, как единое целое. Создатель теории множеств немецкий математик Георг Кантор (1845 – 1918) дал такую формулировку: «Множество есть многое, мыслимо нами, как целое».

В математике употребляются следующие синонимы термина «множество»: семейство, класс, семейство, область, совокупность. В описываемой теории множеств игнорируется природа отдельных объектов, составляющих множество, а изучаются свойства, присущие каждому множеству, способы образования множеств и т.п.

Объекты, составляющие множество – объекты нашей интуиции или интеллекта – могут быть самой различной природы. Например, множество естественных спутников Земли, множество студентов второго курса, множество букв русского алфавита, множество арабских цифр, множество натуральных чисел и т.д. Однако в математике чаще рассматриваются множества, состоящие из чисел, кривых, множеств чисел и т.д.

Определение. Объекты, составляющие множество, называются его элементами или членами. Можно сказать, что множество – это совокупность различимых элементов. Подчеркнем, что, согласно данному описанию, во множестве не бывает одинаковых (неразличимых) элементов.

Пример 1. Приведем примеры наиболее важных числовых множеств и зафиксируем для них обозначения (множества будем обозначать прописными буквами латинского алфавита, а их элементы – строчными):

N – множество целых положительных чисел;

N0 – множество натуральных (неотрицательных) целых чисел (0 не относится к натуральным числам);

Z – множество целых чисел;

Q – множество рациональных чисел;

R – множество действительных чисел;

6

C – множество комплексных чисел.

Если М – множество, а а – его элемент, то пишут а М (читается: «а принадлежит М»), если же а не есть элемент множества М, то пишут а М, или a M (читается: «а не принадлежит множеству М»). Например,

2 N0, 4 Z, –2 N0, 2-1 R, 2 Q, 2 R, 1 i C, 1 i R .

Определение. Множество, не содержащее ни одного элемента, называется пустым и обозначается . Иногда пустое множество обозначают 0 или .

В общем случае множества бывают конечными и бесконечными. Определение. Конечное множество – это такое множество, для ко-

торого существует натуральное число, являющееся числом его элементов. Конечное множество, содержащее в качестве элементов только объекты а1, a2,…, an, обозначается {а1, a2,…, an}. Отметим, что {а} – множество, состоящее из единственного элемента а, называется одноэлементным множеством.

Определение. Множество, не являющееся конечным, называется бесконечным.

За основу для сопоставления бесконечных множеств принято брать натуральный ряд чисел N: 1, 2,…, n.

Определение. Если бесконечное множество оказывается возможным привести во взаимно однозначное соответствие с натуральным рядом чисел, то такое множество называют счетным.

Определение. Если бесконечное множество невозможно привести в соответствие с натуральным рядом чисел, то такое множество называют

несчетным.

Приведем несколько примеров счетных множеств:

1.Множество квадратов целых чисел 1, 4, 9, …, n2 представляет собой лишь часть (подмножество) множества натуральных чисел N. Однако множество является счетным, так как приводится во взаимно однозначное соответствие с натуральным рядом путем приписывания каждому элементу номера того числа натурального ряда, квадратом которого он является.

2.Счетным является множество Z целых чисел – положительных и отрицательных, хотя натуральный ряд представляет собой лишь часть (подмножество) этого множества. Это можно установить, рассмотрев однозначное соответствие:

из которого следует, что

7

Из приведенных примеров видно одно замечательное свойство бесконечных множеств – возможность приведения во взаимно однозначное соответствие бесконечного множества с его бесконечным же подмножеством, которое не имеет места в случае конечных множеств.

Существование несчетных множеств следует из теоремы, доказанной Георгом Кантором.

Теорема. Множество всех действительных чисел интервала 0 < x 1 несчетно.

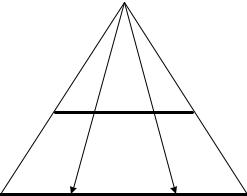
Следствие. Несчетное множество – множество действительный чисел любого интервала (a, b], что можно отобразить на рисунке путем проекций (рис. 1).

x y

Рис. 1. Проекция несчетного множества на интервал (a, b] действительной оси

Определение. Если А – конечное множество, то мощностью множества А называется число его элементов и обозначается |А|. Число элементов пустого множества равно 0.

Определение. Два множества M и N называются равными, если они состоят из одних и тех же элементов.

Если множества M и N равны, то пишут M = N, в противном случае M N. Таким образом, M N, если в множестве М есть элемент, не принадлежащий N, либо, наоборот, в N есть элемент, не принадлежащий М.

Согласно данному определению равенства множеств, все пустые множества равны или, иначе, существует только одно пустое множество.

Задача 2. Равны ли множества:

а) {0, 1, 2} и {0, 2, 1}; б) {0, 1} и {{0, 1}}?

8

Ответ. а) Так как множества {0, 1, 2} и {0, 2, 1} состоят из одних и тех же элементов, то {0, 1, 2} = {0, 2, 1}.

б) Множества {0, 1} и {{0, 1}} не равны, так как первое – двухэлементное, а второе - одноэлементное (следует также различать множество {a} и сам объект а).

Задача 3. Даны три множества: А = {0, 1}, B = {{0, 1}, 2} и C = {{{0,

1}, 2}, 3}. Верны ли соотношения: а) А В; б) В С; в) А С? Ответ. а) да; б) да; в) нет.

Задача 4. Пусть А есть множество всех натуральных четных чисел больше 0, а В – множество всех натуральных чисел, представимых в виде суммы двух нечетных натуральных чисел. Доказать, что А = В.

Решение. Для этого покажем, что каждый элемент А есть и элемент В, и наоборот, каждый элемент В является и элементом А.

Пусть сначала х А. Докажем, что х В. Если х А, то x = 2k, k 1. Так как x = 2k = (2k – 1) + 1, где 2k – 1 N0, потому что k 1, то х В. Обратно, если х В, то x = (2k – 1) +(2m – 1), где 2k – 1 1 и 2m – 1 1, потому что 2k – 1 и 2m – 1 – нечетные натуральные числа. Следовательно, x = 2(k + m – 1), где k + m – 1 1, и, значит, х А.

Таким образом, доказано, что множества А и В состоят из одних и тех же элементов.

Существуют три основных способа задания множеств:

1.Перечисление. Множество можно задать, перечислив все его элементы. Такой способ удобен при малом числе элементов. Перечислением можно задать, естественно только конечное множество, хотя иногда проще задать его описанием.

2.Описание – задание такого свойства, которым обладают только

элементы рассматриваемого множества. Например, трудно перечислить все натуральные числа от 2 до 2n, а описание содержится в выделенных словах.

3.Задание порождающих процедур. Порождающая процедура описывает способ получения элементов множества из уже имеющихся элементов или других объектов. Тогда элементами множества считаются все объекты, которые могут быть построены с помощью такой процедуры.

Разумеется, бесконечные множества можно задать только последними двумя способами.

Пример 5. Для множества M2n = {1, 2, 4, 8, 16,…} порождающая

процедура определяется двумя правилами: а) 1 M2n; б) если m M2n, то 2m M2n, а для множества M = {314, 159, 265,…} порождающее правило следующее: а) механизм вычисления числа ; б) выделение цифр по 3.

Введем часто используемый способ обозначения множеств. Пусть р(х) – одноместная высказывательная форма, где х – переменная, областью

9

значения которой является множество М. Тогда через {x M | р(х)} обозначается множество, состоящее из всех тех и только тех элементов а M, для которых высказывание р(а) истинно. Выражение {x M | р(х)} читается так: «множество всех таких х, принадлежащих М, что р(х)».

Задача 6. Перечислите все элементы множества, заданного описани-

ж) {y, k Z | (y > 0)&(y = 2k +1}.

Ответ. а) {3}; б) {6, 7, 8, 9}; в) {-1, 0, 1}; г) Z; д) ; е) {0, 12, 27}; ж) {1, 3, 5 ,7,…} – множество всех натуральных нечетных чисел.

Задача 7. Задайте с помощью описания характеристических свойств:

{x Z | x 0}.

Задача 8. Задайте перечислением всех элементов множества, заданные с помощью описания характеристического свойства:

10) {x Z | |x| 2}.

Ответ. 1) M = {1, 2, 3, 4}; 2) M ={1, 2, 3, 4}; 3) M ={0, 1, 2, 3, 4, 5}; 4) M ={0, 1, 2, 3, 4, 5}; 5) M ={0}; 6) M = ; 7) M ={1}; 8) M ={-1, 0, 1}; 9) M ={1, 2}; 10) M ={-2, -1, 0, 1, 2}.

Задача 9. Можно ли задать перечислением всех элементов множе-

Ответ. 1) Да; 2) Да; 3) Да; 4) Да; 5) Нет; 6) Да; 7) Нет; 8) Да.

10