Доказать теоремы Лагранжа, Коши и Лопиталя.
Теорема Лопиталя
Пусть
функции
и
непрерывны и дифференцируемы в некоторой
проколотой окрестности
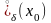точки
,
причем
,
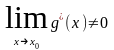и
.
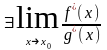Тогда
.
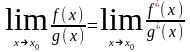Доказательство:
Рассмотрим
окрестность
.
(Рисунок) Выберем последовательность
.
Тогда, начиная с некоторого номера N,
члены последовательности попадают в
эту окрестность. Тогда, так как
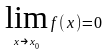и
,
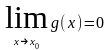то функции
и
в точке
имеют устранимый разрыв. Доопределим
эти функции до непрерывности:
,
.
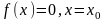Тогда на отрезке
данные функции непрерывны и дифференцируемы
на интервале
.
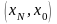Таким
образом, выполняются все условия теоремы
Коши. Это
значит, что
,
где
,
или
.
Перейдем
к пределу при
:
,
. ■
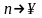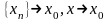Замечание.
Если
не существует, то из этого не следует,
что не существует
.
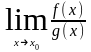Пример.
Вычислим
,
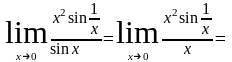
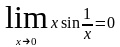но
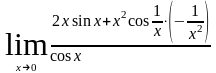не существует.
Пример.
Вычислим
.
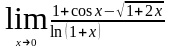Применяя правило Лопиталя, получим
.
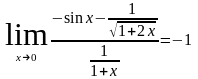Замечание.
Теорема Лопиталя
сформулирована для неопределенности
типа
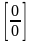и имеет место для неопределенностей
типа
Теорема Лагранжа
Пусть
функция
непрерывна на отрезке
и дифференцируема на интервале
,
тогда найдется точка
.
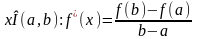Доказательство:
Введем
вспомогательную функцию
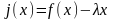так, чтобы функция
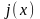удовлетворяла теореме Ролля, т.е.
:
,
,
.
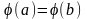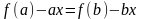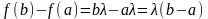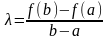Тогда
,
,
.
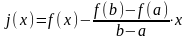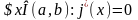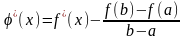Таким образом,
■
Теорема Коши
Пусть
функции
и
непрерывны на отрезке
и дифференцируемы на интервале
,
причем
.
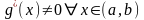Тогда
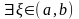такая, что
.
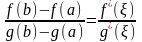Доказательство:
Докажем
сначала, что
.
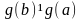Функция
удовлетворяет условиям теоремы Лагранжа,
значит, что
.
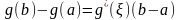Отсюда
.
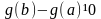Введем
вспомогательную функцию
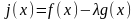так, чтобы она удовлетворяла условиям
теоремы Ролля.
.
Тогда
.
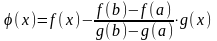Отсюда
.
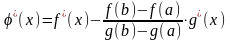Таким образом,
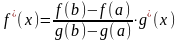или
.
■
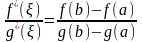Замечание. Теорема Коши является наиболее общей теоремой, т.е. теорема Ролля и Лагранжа являются следствиями из теоремы Коши.
Замечание. Геометрический смысл теоремы:
точка
,
в которой касательная к графику функции
имеет такой же наклон, как и хорда,
соединяющая точк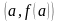и
и
.
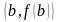(Рисунок)
.
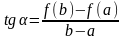Замечание. Теорема Лагранжа является обобщением теоремы Ролля.
Доказать формулу Тейлора.
Формула Тейлора
Можно
заметить, что чем больше производных
совпадают у двух функций в некоторой
точке, тем лучше эти функции аппроксимируют
(приближают) друг друга в окрестности
этой точки. Нас будет интересовать
приближение функции в окрестности одной
точки с помощью многочленов. Рассмотрим
многочлен степени
:
.
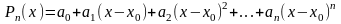Заметим, что
.
Так как
,
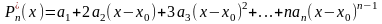то
.
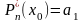Аналогично получим
,
.
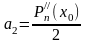Определение
1. Функция
называется гладкой
порядка
в точке
на интервале
,
если она имеет все производные порядка
включительно, причем эти производные
являются непрерывными функциями на
отрезке
.
Этот факт
обозначается
.
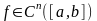Определение
2. Выражение
вида
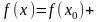
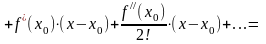
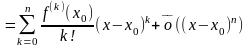называется
формулой
Тейлора
для функции
в окрестности точки
.
Теорема 1. Если функция является гладкой порядка в некоторой окрестности точки , то имеет место формула Тейлора для данной функции .
Доказательство:
Пусть
имеет место формула Тейлора для функции
:
,
причем
,
,
.
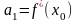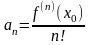Обозначим
.
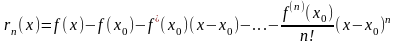Используя
правило Лопиталя, покажем, что
.
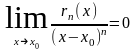Так как
,
…,
,
,
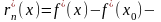
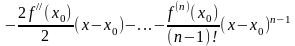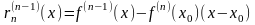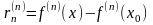тогда
=
=…=
.
■
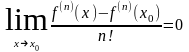Замечание. В формуле Тейлора первое слагаемое называют главной частью функции, а второе – остаточный член функции