Сложение и вычитание векторов. Умножение вектора на число.

Векторная алгебра - раздел математики, изучающий векторы. Векторная алгебра является одним из основных средств исследования в физике и разных разделах математики. В векторной форме записываются многие законы физики и механики, И в геометрии аппарат векторов позволяет кратко записывать формулировки задач и их решения, например, теорема о средней линии треугольника в векторной форме записывается так

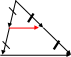А , а доказывается в одну строку:

К L

В С

Чтобы объединить преимущества координатного и векторного методов, для векторов введены координаты. Это позволяет свести действия с векторами к аналогичным действиям с их координатами, и проводить действия с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные множители.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Линейными операциями над векторами называют операции сложения, вычитания и умножения вектора на число.

Действия с коллинеарными векторами

В графической форме: если векторы , и отложить последовательно от некоторой точки А , то суммой векторов + + является вектор , начало которого совпадает с точкой А, а конец совпадает с концом вектора .

Полученный результат не зависит от выбора точки А.

М

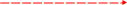А

+ + - =

Действия с неколлинеарными векторами

В графической форме действия с неколлинеарными векторами выполняются по правилам треугольника и параллелограмма, а в пространстве по правилу параллелепипеда.

При сложении двух векторов оба слагаемых и результирующий вектор лежат в одной плоскости (почему?).

Если два вектора являются сторонами параллелограмма, то одна из диагоналей этого параллелограмма представляет сумму этих векторов, а вторая – разность.

В С В - В

+

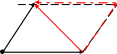
А D

А D

Или по правилу треугольника:

Пусть материальная точка А переместилась сначала в точку В, а затем в точку С. В результате двух перемещений, которые можно представить векторами и точка А переместилась из точки А в точку С.

С Т.е. = +

А В

Операция сложения векторов определяется следующим образом: чтобы сложить два вектора, необходимо от конца первого вектора отложить второй вектор и начало первого вектора соединить с концом второго.

Для операции сложения векторов справедливы свойства, аналогичные свойствам сложения чисел:

1. Переместительный закон:

+ = + (правило параллелограмма)

+ = + =

2. Сочетательный закон: + ( + ) = ( + ) +

С = + = + = ( + ) +

В

= + = + = + ( + )

А D

Сложение нескольких векторов производится следующим образом:

– от некоторой удобной точки откладывается первый вектор, от конца первого вектора откладывается второй и т.д.

– начало первого вектора соединяется с концом второго, и этот вектор является суммой всех слагаемых векторов.

А АВ = + + + +

В

Разностью векторов и называется такой вектор , сумма которого с вектором , равна вектору , или: разность векторов и это сумма вектора и вектора –

–

– +(– )

–

Произведение вектора на скаляр (число) называется вектор · (или · ), который имеет длину · , коллинеарен вектору , имеет направление вектора , если > 0 и противоположное направление, если <0.

1 . Если дан вектор , то векторы 3 и - 2 будут иметь вид: 3 - 2

2 . Для данных векторов и постройте векторы; а) + 2 ; б) 2 + ; в) –

В А

а); = + 2 б) = 2 + ;

А

в) – = + (– )

–

–

+ (– )

3. В треугольнике АВС укажите векторы: а) + ; б) + ;

К С М а) + =

б) + =

в) + =

А В

4. В параллелограмме АВСD О - точка пересечения диагоналей АС и ВD. Найти +

D С С

О О

А В + = В

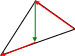
5. В треугольнике АВС АD - медиана. Найти -

А

С

D

В

- = + =

6. На стороне СD квадрата АBСD лежит точка Р так, что СР = РD, О – точка пересечения диагоналей. Выразите векторы , , через векторы = и = .

B С

О Р = = ; = =

А D = = ( + ) = ( + )

= + = +

+ = = – = – – = – ; = – ;

7. На стороне BС ромба АBСD лежит точка K так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы = и = .

B К С

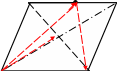АBСD – ромб = = и = =

= =

О = + = +

А D = = ( + ) = ( + )

8. В параллелограмме АВСD О - точка пересечения диагоналей АС и ВD. АК = КО. Выразить

через и

D С Если два вектора являются сторонами параллелограмма,

то одна из диагоналей этого параллелограмма

О представляет сумму этих векторов = + ,

К а вторая – разность: = -

А В = = ( - )

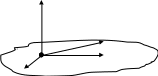
Некомпланарными являются три вектора, не лежащие в одной плоскости

D Векторы , , - компланарные, так как лежат

в одной плоскости.

Векторы , , , - не компланарные, так как

точки D, М, N не лежат в одной плоскости.

М

О N

В

Для сложения трех некомпланарных векторов пользуются правилом параллелепипеда – пространственным аналогом правила параллелограмма.

Пусть векторы ; и некомпланарны. Отложим их от одной точки О. Тогда, сумма + - диагональ параллелограмма: . Но векторы и отложены от

одной точки О, т.е. их также можно сложить, пользуясь правилом параллелограмма.

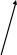
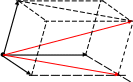
О

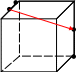
1. В кубе ABCDA₁B₁C₁D₁ = , = , = , A₁М = МD₁; СN = NC₁; АS =АD

D₁ C₁ Выразить векторы и

М B₁ N

A₁ D₁ C₁

N М D С

D С N S

S

A B = + - = + +

2. В правильной треугольной призме ABC все ребра равны 1. A₁К = КС₁.

Найти -

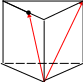A₁ B₁ - = + = =

т.к. тр-к A₁ B₁C₁ - правильный и B₁ К - высота в нем

К C₁

A B

C

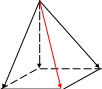
3. В пирамиде АBCDМ основание - параллелограмм, = , = , = . Выразить вектор через векторы , , .

А = + , но: = а вектор выразим

через и :

+ = = -

тогда: = + - = + -

B D

C М

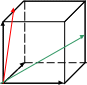
4. ABCDA₁ B₁C₁D₁ - куб. AD = ; АВ = ; АА₁ = . Выразить и

D₁ C₁

К

B₁

A₁ М = + = + +

D C

A B

Письменно ответьте на вопросы:

1. Сформулируйте правило параллелограмма, треугольника. Параллелепипеда

2. Как изображается противоположный вектор?

3. Какой векторный смысл имеют диагонали параллелограмма?

4. Когда два направленных отрезка изображают один и тот же вектор?

Выполните задания:

1. Что можно сказать о векторах - + и - + ?

2. Докажите, что в правильном пятиугольнике АBCDЕF сумма пяти векторов с началом в центре этого пятиугольника и с концами в его вершинах равна нулю.

3. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ показать вектор, равный

+ + +

4. Дан параллелограмм АВСD, точки Е и F лежат на сторонах АD и ВС. АЕ = ЕD, ВF : FС = 4 : 3. Выразите вектор через векторы = и = .

5. ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед. = ; = ; =

Найти - ; - ; -

6. В прямоугольном параллелепипеде показать векторы: = +

= - = 2 +

7. В параллелепипеде ABCDA₁ B₁C₁D₁ разложить: вектор по векторам , и

8. В тетраэдре ABCD точки K и L - середины ребер AB и CD. Определить

9. В правильной треугольной призме ABСА₁В₁С₁ сторона основания равна 1, точка Е - середина А₁С₁. Найдите | - |

10 Точка К не лежит в плоскости треугольника ABC. Е и Р - середины отрезков AB и ВС. Выразите вектор - через вектор .

ДЕЙСТВИЯ С ВЕКТОРАМИ, ЗАДАННЫМИ СВОИМИ КООРДИНАТАМИ

Рассмотрим принцип сложения векторов на примере плоской системы координат.

1. Найти координаты вектора , если = +

С { (х_В – х_А); (у_В – у_А);( z _В – z_А) }

В

{ (х_С – х_В); (у_С – у_В); ( z _С – z_В) }

А х_А х_В х_С х

Легко заметить, что х_С – х_А = ₍х_В – х_А) + ( х_С – х_В) = пр_Ох + пр_Ох

очевидно, у_С – у_А =( у_В – у_А) + (у_С – у_В ) = пр_Оу + пр_Оу

В пространстве сложение производится по тем же правилам, что и в планиметрии, лишь дополнительно появляется третья координата.

Пусть = а_х + а_у + а_z и = b_х + b_у .+ b_z . Тогда, так как сложение векторов сводятся к выполнению соответствующих линейных операций с проекциями этих векторов, то можно записать:

± =(х₁ ± х₂) + (у₁ ± у₂) т.е. при сложении векторов их координаты складываются

{- 2; 4; 2 } и { 4; 3; 0 } = + { 2; 7; 2 }

Рассмотрим принцип умножения вектора на число на примере плоской системы координат.

2. Найти координаты вектора 3 .

(ОА_х)

х

О ОА_х ОА_х B_х

= + + =3

При умножении вектора, заданного своими координатами, на число его координаты умножаются на это число.

Т.о. в координатной форме, если = x + y + z п = пx + пy + пz

При этом: векторы п и коллинеарные, их направление совпадает, если k > 0, их направление противоположно, если k <0.

Выполнить действия и ответ записать в координатной форме

1. Найти координаты векторов 2 и , если {-2; 0; 3 }

2 {-4; 0; 6 } {-1; 0; 1,5}

2. Даны векторы = 4 - 3 и = - 3 + ,

Найти координаты вектора , если

= 2 -3 = 8 - 6 - 3( - 3 + ) = 13 - 7 ; {-13; - 7}

= - 2 =- 1,5 + 0,5 - 8 +6 = -9,5 + 6,5 {-8,5; 6,5}

3. Координаты векторов { -2;4;2 } и { 4; 3;0 }

Найти координаты вектора : = 3 - 2

{ -6 -8; 12 - 6;6 }; { -14; 6;6 }

Если координаты векторов пропорциональны, то векторы коллинеарные.

Т.е., если = x₁ + y₁ + z₁ ; = x₂ + y₂ + z₂ и значит,

векторы и коллинеарные

4 Даны векторы = 2 - 4 и { 3;-1; -2} . Найти значения т и п, при которых векторы = -3 и {т + п; -3; т - п } коллинеарные.

Определяем координаты вектора -3

{ 2; 0; - 4 } { 1; 0; - 2 } ; { 3;-1; -2} 3 { 9;-3; -6 }

= -3 { - 8; 3; 4 }

в екторы коллинеарные = = 3т - 3п = -12

3т + 3п = -24

6т = -36, т = - 6

- 6п = 12, п = - 2

5. Даны точки А(2; -1; 0); В(-3; 2; 1) и С(1;1;1). Найти координаты точки D, если = -2

{ (x_B – x_A); (y_B – y_A);(z_B – z_A) } {-5; 3; 1} ; -2 {10; -6; -2}

{ 10; -6; -2} x_D – x_С = 10 x_D =11; y_D – y_С = -6 y_D = -5; z_D – z_С = -2 z_D = -1

D(11; -5; -1)

6. Даны точки А(-3;1; -1); В (2;-4; 1) , выразить через орты вектор и вычислить его длину.

{ (x_B – x_A); (y_B – y_A);(z_B – z_A) } {5; -5;2} 5 -5 + 2 ;

| | = = = =3

7 Даны векторы = - 3 + и = -2 + . Найти координаты вектора = -

{ 1;-3; 1} ; { -1; 0; 1}

= - { 3;-3; 0}

8. Даны точки А( 1;2; -1); В (-2; 1; 1) . Вычислить расстояние от начала координат до середины отрезка АВ

С( ; ; ) С(- 0,5; 1,5; 0)

| | = = =

Письменно ответьте на вопросы:

1. Как в координатной форме выполняется сложение векторов? Умножение вектора на число?

2. Как вычисляется длина вектора, заданного в координатной форме?

3. Как записать сложение векторов (умножение вектора на число) в форме разложения по ортам?

Выполните задания:

1. Даны точки А(-3; 1; -1) и В(2;-4; 1). Выразить через орты вектор и вычислить его дину.

2. Вычислить координаты вектора = - , если = 2 - 5 + 3 ; = -2 + - 3 .

3. Даны точки А(1; 2; -1) и В(-2; 1; 1). Вычислить расстояние от начала координат до середины отрезка АВ.

4. Даны точки А(0; -1; 2) и В(- 1; 4; 1); С(- 2; 1; 0); D(-2; 1; 0).

Вычислить координаты вектора т = + .

5. Выразить через орты вектор = - , если = - 3 + 2 ; = 2 - - 2 .

6. Вычислить длину вектора = (2 ) - ( ), если = (2;3;1); = (0; 1; 1).

7. Вычислить длину вектора = 2 + , если = - + ; = - - .

8. На векторах и построен параллелограмм. Выразить в ортах его диагонали, если

= + , = -3

9. Доказать коллинеарность векторов { ; ; - }; { ; ; - };

10. Выяснить, будут ли векторы { 1; -2; 0 } ; = 2 + 3 - и =3 - 2 коллинеарными.