Координаты вектора

Координаты точки – это числа, соответствующие ее проекциям на оси координат. Проекциями произвольного отрезка на оси координат являются проекции этого отрезка на оси координат.

Для вектора , имеющего начало в точке О(0;0), координаты точки А являются

координатами вектора. Записывается: { х_А; у_А }. Такая запись называется: «Запись вектора в координатной форме». Пусть А(3;2), тогда { 3;2 }.

При выполнении действий с векторами единицы масштаба

у называют координатными векторами (ортами) и обозначают: по оси

абсцисс, и по оси ординат и по оси аппликат. В нашем случае = 3 =2 (на плоскости)

проекция вектора на ось 0х равна 3 ; на ось 0у равна 2 .

у_А А (3;2)

И по правилу сложения векторов = х + у .

Такая запись называется: «Разложение вектора по ортам»

в нашем случае = 3 + 2 .

0 х_А х

Если начало вектора не совпадает с началом координат, то координатами вектора являются его проекции на оси координат: (х_В– х_А , у_В– у_А). И тогда в координатной форме вектор записывается: { (х_В–х_А); (у_В–у_А) }. В нашем случае: А(1;3), В (4;5), и в координатной форме вектор записывается: { 3; 2 }, а его разложение по ортам: = 3 + 2 .

у

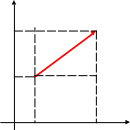
у_В В (4;5) В прямоугольном треугольнике АСВ: катеты АС и ВС,

гипотенуза - вектор { 3; 2 }, и по теореме Пифагора

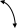у длина вектора, или его модуль вычисляется по формуле

| | = , (1 ) если

у_А А(1;3) С заданы координаты точек А и В;

или | | = , (2) если

вектор задан в координатной форме или в виде

0 х_А х х_В х разложения по ортам.

Е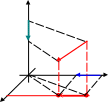 сли 0х, то проекции точек А и В совпадают и проекция вектора ось 0х равна 0

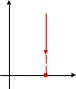у z Для трехмерного пространства

пр._Оz

пр._Оу

0 у

0 х

На плоскости пр._Ох = 0

х

Для трехмерного пространства во всех формулах добавляется третья координата:

{ (х_В–х_А); (у_В–у_А);(z_B - z_A)},

= x + y +z

| | = .

Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью: пр._Ох = | | ·cos .

Проекция вектора на ось положительное число (+),если

направление вектора совпадает с положительным направлением оси,

х т.е. = пр._Ох = | | ·cos .

Проекция вектора на ось отрицательное число (–),если

вектор и ось имеют противоположные направления.

или если < < π пр._Ох = - | | ·cos .

х

1. Проекции равных векторов на одну и ту же ось равны.

2. В данной системе координат каждый вектор имеет единственный набор координат.

3. Координаты вектора, отложенного от произвольной точки, равны разности соответствующих координат его конца и начала.

4. Векторы параллельны (коллинеарные) тогда и только тогда, когда их координаты пропорциональны

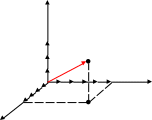1. Записать координаты вектора: = 4 + 5 + 3 z

= 4 + 5 +3 { 4; 5; 3}

Графически это означает: 3

А (4;5; 3)

0 5 у

4

х А₁(4;5)

2. Записать координаты векторов:

= – 4 + – { –4; 1; –1 }

= – 2 + { 0; – 2; 1 } ; = + { 0; 1; 1}

= – {–1; 0; 1 }; = 0,7 { 0; 0; 0,7}

3. Если вектор отложен от начала координат, то координаты вектора равны координатам конца вектора. Векторы ₁ ; ₁; ₁; ₁ в этом случае называются радиус-векторами.

У прямоугольного параллелепипеда ОА = 2, ОС = 3, ОО₁ = 2.

Найдите координаты векторов ₁ ; ₁; ₁; ; ; ;

z

O₁ А₁ (2; 0; 2) ₁ { 2; 0;2 } ₁ = 2 + 2 ,

С₁

A₁ В₁

₂

O ₃ С В₁ ( 2; 3; 2) ₁ { 2; 3; 2} ₁ = 2 + 3 + 2

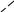₂ у

х A B О₁( 0; 0; 2) ₁ { 0; 0; 2} ₁ = 2 ,

С₁(0,3;2); О₁(0,0;2); А(2,0;0); С(0,3;0); В( 2; 3; 0)

{ - 2,3; 2 } ; {- 2, 0; 2 } ; { 0; 3; -2}

4. Найти длину радиус- векторов , , , если А(0,2;5); В(-1; 3; ); С(3; -2; 2 ).

| | = = =

| | = = = 4

| | = = = 5

5. Даны две координаты вектора {4; -12; z } . Найти его третью координату, если: | | =13

| | = 13² = 16 + 144 + z² z² = 9 z = ± 3

6. Какие координаты имеет вектор , если А(1;2;3): = + 2 + 3

А(-5;4;-1): = -5 + 4 -

7. Назовите координаты векторов: а) = – 2 + 6 ={ – 2; 6 }

б) = + 3 { 1; 3} в) = – 3 { 0;– 3} d) = – 5 { –5; 0}

8. Разложите по координатным векторам , если А(0;0;2) и С(0;2;0)

= 0 + 2 –2 , = 2 –2

8. Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов

; ; { 2; –3: 0} { 7; –12; 18 } { –8; 0; 5}

Письменно ответьте на вопросы

1. Что называется вектором?

2. Что называется модулем вектора?

3. Какие векторы называются нулевыми? Равными?

4. Какие векторы называются коллинеарными? Компланарными?

5. Что называется координатами вектора?

6. В каком случае координата вектора равна нулю?

7. Сформулируйте признак коллинеарности векторов.

8. В каком случае все три координаты вектора равны нулю?

9. Что называется разложением вектора по координатным векторам?

10. Что означают числа х, у, z при записи вектора в координатной форме?

11. Какова связь между проекцией вектора на ось, модулем вектора и углом между вектором и координатной осью?

Выполните задания:

1. Даны векторы { 3; 2; 1} ; { 1; –3; 5 } ; { – ; 0,75; –2 } . Запишите координаты точек А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5).

2. Запишите в координатной форме ВС, если С(-2; 1; 3); В(3; -2; 1)

3. Вершины куба имеют координаты А(3;-1;1); В(-1;-1;1); С(-1; 3; 1); С₁ (-1; 3; 5).

а) найдите координаты вершин В₁ и D₁

б) разложите по координатным векторам векторы: и

4. Векторы и равны. Найдите координаты точки А, если { – 1; 2; 4 } и С(2;0;5)

5. Определить, при каких значениях т векторы и равны, если { 2т; 2 } и {т; 1}.

6. Найдите значения т и п, при которых векторы и удут коллинеарными, если { 1; – 2; т },

{ п; 6; 3 }.

7. Векторы { 10; т; 5 } и { п; 3; 2} коллинеарные. Найти значения т и п .

8. Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов

; ;

9. Найти координаты вершины D параллелограмма АВСD, если А(3; 0; 1); В(4; 2; –1); С (1; 2; 5);

10. Проверить, являются ли точки А(– 4; – 4); В(–3; 4); С (4; 5); D(10; –2) вершинами трапеции

АВСD.