
- •Элементы линейной алгебры
- •0 УМ у ось ординат
- •Преобразование координат
- •Координаты вектора
- •Сложение и вычитание векторов. Умножение вектора на число.
- •Скалярное произведение векторов
- •Уравнение прямой
- •Уравнение плоскости
- •Комплексные числа и арифметические операции над ними. Тригонометрическая форма записи комплексного числа
- •Действия над комплексными числами в алгебраической форме
Преобразование координат
Переход от одной системы координат в другую называется преобразованием системы координат.
Мы будем рассматривать два случая преобразования системы координат, и выведем формулы зависимости между координатами произвольной точки плоскости в разных системах координат. (Методика преобразованием системы координат аналогична преобразованию графиков).
1. Параллельный перенос. В этом случае меняется положение начала координат, а направление осей и масштаб остаются неизменными.
Если начало координат переходит в точку 01 с координатами 01(х0; у0), то для точки М(х;у) связь между координатами системы х0у и х00у0 выражена формулами:
х = х0 + х'
у = у0 + у'
Полученные формулы позволяют найти старые координаты по известным новым х' и у' и наоборот.
у'
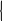
 у
М(х;у)
у
М(х;у)
![]() М(х'; у')
М(х'; у')
у'
01 (х0; у0), х'
у у0
0 х
х0 х'
х
2 .
Поворот
осей координат.
В этом случае обе оси поворачиваются
на один и тот же угол
.
Поворот
осей координат.
В этом случае обе оси поворачиваются
на один и тот же угол
![]() ,
а начало координат и масштаб остаются
неизменными.
,
а начало координат и масштаб остаются
неизменными.
у
М(х;у)
у1 х1
r
Координаты точки М в старой системе М(х;у) и М(х'; у') - в новой. Тогда полярный радиус в обеих системах одинаков, а полярные углы соответственно равны + и , где - полярный угол в новой системе координат.
П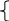 о
формулам перехода от полярных координат
к прямоугольным имеем:
о
формулам перехода от полярных координат
к прямоугольным имеем:
x = rcos( + ) x = rcos · cos - rsin ·sin
y = rsin( + ) y = rcos · sin + rsin · cos
н о rcos = х' и rsin = у', поэтому
x = х' · cos - у'·sin
y = х' · sin + у'· cos

Письменно ответьте на вопросы:
Что называется прямоугольной системой координат на плоскости? в пространстве?
Какая ось называется осью аппликат? Ординат? Абсцисс?
Каково обозначение единичных векторов на осях координат?
Что называется ортом?
Как вычисляется в прямоугольной системе координат длина отрезка, заданного координатами своих концов?
Как вычисляются координаты середины отрезка, заданного координатами своих концов?
Что называется полярной системой координат?
Какова связь между координатами точки в прямоугольной и полярной системах координат?
Выполните задания:
1. На каком расстоянии от координатных плоскостей находится точка А(1; -2; 3)
2. На каком расстоянии находится точка А(1; -2; 3) от координатных прямых а)Оу; б) Оу; в)Оz;
3. Какому условию удовлетворяют координаты точек пространства, одинаково удаленных:
а) от двух координатных плоскостей Оху и Оуz; АВ
б) от всех трех координатных плоскостей
4. Найдите координаты точки М середины отрезка АВ, А(-2; -4; 1); В(0; -1; 2) и назовите точку, симметричную точки М , относительно а) оси Ох
б) оси Оу
в) оси Оz.
5. Дана точка В(4; - 3; - 4). Найдите координаты оснований перпендикуляров, опущенных из точки на оси координат и координатные плоскости.
6.На оси Оу найти точку, равноудаленную от двух точек А(1; 2; - 1) и В(-2; 3; 1).
7. В плоскости Охz найдите точку, равноудаленную от трех точек А(2; 1; 0); В(-1; 2; 3) и С(0;3;1).
8. Найдите длины сторон треугольника АВС и его площадь, если координаты вершин: А(-2; 0; 1), В(8; - 4; 9), С(-1;2; 3).
9. Найдите координаты
проекций точек А(
2; -3;
5); В (3;-5;![]() );
С( -
;
-
);
С( -
;
-![]() ;
;
![]() -
).
-
).
10. Даны точки А(1; -1; 0) и В(-3; - 1; 2). Вычислите расстояние от начала координат до данных точек.
![]()
ВЕКТОРЫ В ПРОСТРАНСТВЕ. ОСНОВНЫЕ ПОНЯТИЯ
Все величины, с которыми имеют дело в физике, технике, обыденной жизни разделяют на две группы. Первые полностью характеризуются своим численным значением: температура, длина, масса, площадь, работа. Такие величины называются скалярными.
Другие величины, например, сила, скорость, перемещение, ускорение и т.д. определяются не только своим числовым значением, но и направлением. Называются такие величины векторными, или векторами. Векторная величина геометрически изображается в виде вектора.
 Вектор -
это направленный прямолинейный отрезок,
т.е. отрезок, имеющий
определенную длину и направление.
Вектор -
это направленный прямолинейный отрезок,
т.е. отрезок, имеющий
определенную длину и направление.
Вектор изображают стрелкой, которая показывает его направление.
Если А
- начало вектора, а В
- его конец, то вектор обозначается
символом
![]() или
или
![]()


 В
- конец
вектора
А
В
- конец
вектора
А
А - начало вектора или В
вектор
![]()
Точки А и В, ограничивающие вектор, играют различную роль. Вектор называется противоположным вектору . Вектор, противоположный вектору обозначается – , = -
Любую точку
плоскости также можно считать вектором,
в котором начало вектора совпадает с
его концом. В этом случае вектор называется
нулевым
и обозначается, например,
![]() или
или
![]() ,
или
,
или
![]() .
.
Абсолютной
величиной
вектора,
или модулем,
ненулевого вектора называется длина
отрезка, которым он изображается. Модуль
обозначается
![]() или
или
![]() .
Длина нулевого вектора равна нулю
.
Длина нулевого вектора равна нулю
![]() =
0 Для
ненулевого вектора модуль |
| =
| АВ
|
=
0 Для
ненулевого вектора модуль |
| =
| АВ
|
![]()
 В
D
C
В
D
C
А

•![]()
α
Для выполнения действий с векторами принят ряд терминов.
Коллинеарными
называются векторы
и
![]() ,
если они лежат на одной прямой или на
параллельных прямых; записываются:
a||b
. Коллинеарные
векторы, имеющие одно направление,
называются
сонаправленными:
,
если они лежат на одной прямой или на
параллельных прямых; записываются:
a||b
. Коллинеарные
векторы, имеющие одно направление,
называются
сонаправленными:
![]() и противоположно
направленными, если
их направление различно:
и противоположно
направленными, если
их направление различно:
![]() .
.
Нулевой вектор коллинеарен любому вектору.
Равными называются два сонаправленных вектора, имеющих равные модули. Равные векторы также называют свободными.
Два вектора, равные третьему вектору, равны.
Вектор можно перемещать вдоль прямой, совпадающей с его направлением и переносить его параллельно самому себе в любую точку пространства.

D С
A В ↑↑
|
|=|
![]() |
=
|
=
В параллелепипеде АВСDА1В1С1 D1 изобразить векторы: сонаправленные, противоположно направленные, равные.
три группы коллинеарных, сонаправленных
 D1
C1
векторов:
D1
C1
векторов:
![]() .
. .
.
. .
А1
В1
=
![]() - равные векторы
- равные векторы
D C
А В
D1
C1
Векторы![]()
![]() ;
;
коллинеарные ,
противоположно направленные
,
противоположно направленные
А1 В1
D С
Компланарными называются три вектора, если при откладывании их от одной точки они лежат в одной плоскости.
Любые два вектора - компланарные.
Три вектора, два из которых коллинеарные, - компланарные.

В1
С1
Векторы
![]()
![]() компланарные
компланарные
А1 D1
В С
А D
