0 УМ у ось ординат
хМ
М(х;у;0)
х
ось абсцисс
Каждой тройке чисел х, у, z сопоставляется
одна и только одна точка пространства.
И наоборот, каждой точке пространства
п
лоскость
соответствует
только одна тройка чисел,
образуется
в
которые
называются ее
координатами: М(
хм
; ум;
zм
).
пространстве
осями Ох и Оz
Если точка лежит на координатной плоскости, то одна из ее координат равна 0:
Z
F(0;y;z)
ZF
С(0;0;z)
ZD
D
(x;0;z)
0 (0;0;0)
YF
YE
B(0;y;0)
Если точка лежит в плоскости
Oxy
y
(хорошо
известной прямоугольной системе
X
D
A(x;0;0)
координат),
то у нее существуют две
XE
координаты
x
и
y.
Третьей координаты z
у
E(x;y;0) точки нет, поэтому, если мы хотим показать, что
рассматриваем точку в трехмерном пространстве, то третью координату записывают равной нулю: E(x;y;0); у точки лежащей на плоскости Oуz, нулю равна координата x: F(0;y;z). У точки, лежащей в плоскости Oxz, нулю равна координата у: D(x;0;z ).
У точки, лежащей на оси координат, две из ее координат равны 0: на оси Ох: А(хА; 0;0); на оси Оу: В(0;уВ; 0); на оси Oz: С(0;0;zC)
Любую точку пространства можно рассматривать как вершину прямоугольного параллелепипеда, построенного на его осях координат. Тогда координаты этой точки (проекции точки на оси координат) x; y и z можно рассматривать как измерения прямоугольного параллелепипеда: a, b и c.
z
А3(x;0;z0)
ZA
A2(0;y;z)
- проекция
точки А на
плоскость Oyz.
проекция
т
очки
А A(x;y;z)
на плоскость YA
Oxz
0 у
XA
х A1(x;y;o) – проекция точки А на плоскость Oyx
Пусть
точка А
-
вершина
параллелепипеда, тогда отрезок АО
является его диагональю, и его длина
вычисляется по известной формуле: d2
= a2
+ b2
+ c2,
где
a,
b
и c
–
измерения
параллелепипеда,
и одновременно координаты точки А(х,
у, z),
т.е.
r(АО) =
.
Случай, когда один конец отрезка совпадает с началом координат, весьма редкий и его можно рассматривать как частный случай. В общем виде концы отрезка с началом координат не совпадают. Тогда проекцией произвольного отрезка на ось координат является число, равное разности соответствующих координат проекций на эту ось концов данного отрезка. В пространстве это три отрезка xB - xA ; yB- уA
и zB- zA
у
z
уВ
В
zB
уА
А
0 хА х В х zA
B
х В – хА A
yA yB y
xA
xB
x
Тогда
расстояние между двумя
точками,
заданными своими координатами, равно
корню квадратному из суммы квадратов
разностей одноименных координат
заданных точек
Т.е.
АВ =
ПОСТРОЕНИЕ ТОЧКИ ПО ЗАДАННЫМ КООРДИНАТАМ
При построении точки по заданным координатам, необходимо помнить, что в соответствии с правилами черчения масштаб по оси Ох уменьшается в 2 раза в сравнении с масштабом по осями Оу и Оz.
1. Построить точкy: А(2; 1; 3) хА = 2; уA = 1; z A = 3
а
)
обычно в первую очередь строят проекцию
точки на плоскость Оху.
Отметить точки хA
=2
и уA
=1
и провести через них прямые, параллельные
осям Ох
и
Оу.
Точка их пересечения
имеет
координаты
(2;1; 0)
Построена
точка
A1(2;1;
0.)
А(2; 1; 3)
а) б)
0
уA
=1
хA =2 у
A1(2;1; 0) 0 уA =1 у
х хA =2 A1(2;1; 0)
х
б) далее из точки A1(2;1; 0) восстанавливают перпендикуляр к плоскости Оху ( проводят прямую, параллельную оси Оz) и откладывают на ней отрезок, равный трем: z A = 3.
2. Построить точкy: B(3; - 2; 1) х B = 3; у B = -2; Z B = 1
z
уB = - 2
B(3; -2; 1) О у
B1(3;-2 ) хB =3
х
3
.
Построить точку C(-2;
1; 3)
z
C
(-2; 1; 3)
ХА = -2; YA = 1; ZA = 3
хC
= -
2 C1(-2;1;0)
уA =1 у
х
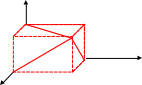
4. Дан куб. А...D1, ребро которого равно1. Начало координат совпадает с точкой В, ребра ВА, ВС и ВВ1 совпадают с положительными лучами осей координат. Назвать координаты всех остальных вершин куба. Вычислить диагональ куба.
z
АВ = ВС = ВВ1 ВD1 = =
В1(0;0;1)
С1
(0;1;1) =
=
А1 (1;0;1) D1(1;1;1)
В(0;0;0) С(0;1;0) у
А(1;0;0) D(1;1;0)
х
5. Постройте точки А(1;1;-1) и В(1; -1;1). Пересекает ли отрезок ось координат? плоскость координат? проходит ли отрезок через начало координат? Найдите координаты точек пересечения, если они есть. z Точки лежат в плоскости, перпендикулярной оси Ох.
Отрезок
пересекает ось Ох
и плоскость хОу
в точке
(1;0;0)
В(1;
-1;1)
0(0;0;0)
у
С(1;0;0)
х
А(1;1;-1)
6. Найти расстояние между двумя точками: А(1;2;3) и В(-1;1;1).
а)
АВ =
=
=
=3
б) С(3;4;0) и D(3; -1;2).
СD =
=
=
В пространстве для определения координат середины отрезка вводится третья координата.
В
( хВ;
уВ;zB
)
С(
;
;
)
А( хА; уА; zA)
7. Найти координаты С середины отрезков: а) АВ, если А(3; – 2; – 7), В( 11; – 8; 5),
хМ = = 7; уМ = = - 5; zМ = = - 1; С(7; - 5; - 1)
8. Координаты точки А(х;у;z). Напишите координаты точек, симметричных данной относительно:
а) координатных плоскостей
б) координатных прямых
в) начала координат
а) Если точка А1 симметрична данной относительно координатной плоскости хОу, то разница в координатах точек будет только в знаке координаты z: А1 (х;у;-z).
точка А2 симметрична данной относительно плоскости Охz, тогда А2(х; -у;z).
точка А3 симметрична данной относительно плоскости Оуz, тогда А2(-х; у;z).
б) Если точка А4 симметрична данной относительно координатной прямой Ох, то разница в координатах точек будет только в знаках координат у и z: А4 (х; -у;-z).
точка А5 симметрична данной относительно прямой Оу, тогда А5(-х; у; -z).
точка А6 симметрична данной относительно прямой Оz, тогда А6( -х; -у; z).
в) Если точка А7 симметрична данной относительно начала координат, то А6( -х; -у; -z).