
- •2)Внутренние силы:
- •6) Деформация при растяжении-сжатии
- •9)Условие прочности
- •11) Механические характеристики материалов
- •20) Момент инерции простых ф-р относ их центральных осей.
- •23) Правило для контроля правильности построения эпюр:
- •24) Чистый изгиб:
- •26) Условие прочности по норм напряж
- •30)Методы начальных параметров для определения прогибов и углов поворота балок
- •44)Практические расчёты на сдвиг
1) В курсе сопр мат из-тся принципы и методы расчётов эле-ов констр-ий на прочность, жёсткость, устойчивость. Прочность – сп-ть эл констр выд-ть нагрузки не разрушаясь. Жёсткость – сп-ть эл констр выд-ть н-ки существенно не изм свои формы и размеры. Устойч-сть – сп-ть эл констр сохр-ть под действием н-ки первонач-ую форму равновесия.
Схематиз св-в материала: 1) материалсчит однородным(св-ва во всех точках одинаковы); 2) материал счит изотропным (св-ва во всех направлениях одинаковы); 3) материал обладает св-вами идеальной уругости (деформир тело полностью восстанавливается после снятия нагрузки); 4) форма и размеры упругого тела прямопропорц изменению нагрузок(подчин з-ну Гука); 5) материал облад. св-вами сплошности ( без пустот заполн пространство ограничен размерами тела)
Эл констр по своим размерам:
1![]()
![]()
![]() .
брус – эл, у которого поперечн сечен
намного меньше его длины. z
– продольная ось, x,y
– поперечные оси (основные). Попер
сечение ┴ продольной оси.
.
брус – эл, у которого поперечн сечен
намного меньше его длины. z
– продольная ось, x,y
– поперечные оси (основные). Попер
сечение ┴ продольной оси.
2. пластина (оболочка) – эл, у кот один р-р много меньше двух др.
3. массив – эл, где все три р-ра соизмеримы.
В![]() иды
нагрузок:
иды
нагрузок:
Сосредоточенные и распределённые:
Сосредоточ-характер как вектор, характер велич, местом прилож и направлением действия.
F![]() – соср-ая сила – счит прилож в одной
точке
– соср-ая сила – счит прилож в одной
точке
m – соср-ый момент
q – интенсивность распр-ой нагрузки – т.е. вел-на н-ки на единицу длины.
2. Поверхностные (силы распространеные по поверхности) и объёмные (силы распредел по объему и действуют на кажд частицу внутри тела (собствен вес, силы инерции)).
3. Статические и динамические: стат нагр приклад медленно с постояным наростанием до конечного значения, динам – резко, могут менять свою величину, место прилож и направл.
Типы опор:
1![]()
![]() .
Шарнирно подвижная опора (опора им одну
связь, т.е. одну реакцию)
.
Шарнирно подвижная опора (опора им одну
связь, т.е. одну реакцию)
2![]() .
Шарнирно неподвижная (две связи – две
реакции)
.
Шарнирно неподвижная (две связи – две
реакции)
3. Жесткая заделка (3 св – 3 р-ции); mA – опорный момент.
Все опорные р-ции опред из ур-ий статики.
2)Внутренние силы:
П![]() од
действием нагр-ок в теле возник внутр
силы (силы упр).
од
действием нагр-ок в теле возник внутр
силы (силы упр).
Внутренние силы – результат взаимодействия элементарных ч-ц обеспечивает целостность тела и совместимость его деф-ции.
Внутр силы опред методом сечений: «Тело рассек на 2 части и рассм-тся равновесие любой из них под действ внешн сил действ-их по одну сторону от сечения и внутр сил действ-их в их сечении».
В![]() нутр
силы заменяют действие отброш-ой части
и тело остаётся в равновесии.
нутр
силы заменяют действие отброш-ой части
и тело остаётся в равновесии.
И![]() з
теоретической механики: «Любую силу
можно перенести ║ приложенной, но её
необходимо уравновесить такой же, но
противоположной по знаку, т.е. приложенную
силу и пару сил (момент)».
з
теоретической механики: «Любую силу
можно перенести ║ приложенной, но её
необходимо уравновесить такой же, но
противоположной по знаку, т.е. приложенную
силу и пару сил (момент)».
Каждую внутр силу к центру тяжести сечения, где и получим результ силу и рез момент.
![]() Разложим
рез силу и момент по коорд осям получим
6 внутр сил.
Разложим
рез силу и момент по коорд осям получим
6 внутр сил.
N – продольная сила (действ вдоль прод оси)
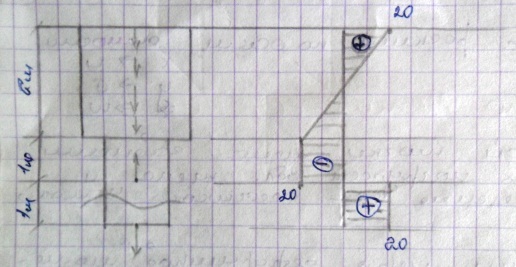
Q![]() X
, QY
– поперечные
силы (┴ прод оси). MX
, MY
– изгибающие моме-нты (изгибают прод
ось). MZ
– крутящий
момент (крутит прод ось).
X
, QY
– поперечные
силы (┴ прод оси). MX
, MY
– изгибающие моме-нты (изгибают прод
ось). MZ
– крутящий
момент (крутит прод ось).
Все внутр силы опред из ур статики:
ΣΖ = 0; ΣΧ = 0; ΣY = 0; ΣMX = 0; ΣMY = 0; ΣMZ = 0.
3![]() )Деформация
тела – измен
формы и разм под действием нагр-ки.
Бывают упругие и пластические. Упругие
– д исчезают после снятия н-ки.
Пластические (остаточные) – остаются
после снятия н-ки. Деф-ции различают
линейные и угловые. Линейные – измен
линейные размеры тела (∆l).
Угловые – изм угловых р-ров тела (γ).
)Деформация
тела – измен
формы и разм под действием нагр-ки.
Бывают упругие и пластические. Упругие
– д исчезают после снятия н-ки.
Пластические (остаточные) – остаются
после снятия н-ки. Деф-ции различают
линейные и угловые. Линейные – измен
линейные размеры тела (∆l).
Угловые – изм угловых р-ров тела (γ).
Простые виды деформации:
1![]() .
Растяжение-сжатие:
.
Растяжение-сжатие:
![]()
2.
Сдвиг:![]() ;
3. Кручение:
;
3. Кручение:
![]()
4.
Изгиб:
![]()
Напряжение–![]() вел-на внутр силы приходящаяся на
единицу площади сечения. В сечении
выделим элем-ную площадку площадью dA.
В ней действ элем-ая сила ∆R.
вел-на внутр силы приходящаяся на
единицу площади сечения. В сечении
выделим элем-ную площадку площадью dA.
В ней действ элем-ая сила ∆R.
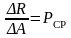 - среднее напряж
по данной площадке.
- среднее напряж
по данной площадке.
Е![]() сли
перейти к пределу, то получим полное
напряженте точки.
сли
перейти к пределу, то получим полное
напряженте точки.
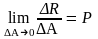 ,
[Па]
,
[Па]
Усилие можно разложить на 2-е сост-ие: ∆N - ┴ составляющая площадки; ∆Q – касательная сост к площадке.
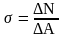 - нормальное
напряжение
- нормальное
напряжение
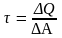 - касательное
напряжение
- касательное
напряжение
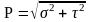 - полное напряжение
- полное напряжение
Внутр усилие можно опр-ть через напряжение, если известны з-ны распред-я напряжений.
В сечении выделим эл-ную площадку dA на расстоянии x, y от коорд осей.Выразим усилие через напряжение

![]()
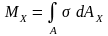 ;
;
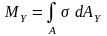
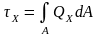 ;
;
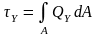
Перемещение- это преход точек тела в новое полож в следств изменен формы и разм тела под действием нагрузки. Перемещение любой точки тела зависит от деформац всех нагруж облост тела и включ в себя перемещ как жесткого целого всех ненагруж частей.
4)Растяжение-сжатие-![]()
![]() такой вид деф эл констр, когда в поперечном
сечении возникает только одна внутр
сила – продольная сила N.
Если внешние силы или их равнод прилож
в центре тяжести сечен прямого бруса
и напр вдоль его прод оси, то возник
центр-ще растяж-сжатие.
такой вид деф эл констр, когда в поперечном
сечении возникает только одна внутр
сила – продольная сила N.
Если внешние силы или их равнод прилож
в центре тяжести сечен прямого бруса
и напр вдоль его прод оси, то возник
центр-ще растяж-сжатие.
Определение внутренних сил
Прод-ая сила N опр-тся методом сечения. Намечаются уч-ки бруса, границей уч-ка явл-ся точки приложения сил. Рассечём уч-к пл-тью и мысленно отбросим одну часть бруса. В сечении прикл-ют прод-ую силу направим её в сторону отбр-ной части, т.е. предположим, что N – растяг-ей сост-щей ур-ия равновесия: сумма всех сил на OZ = 0, из кот опред-ся N. Прод-ая сила N, численно равная алг-кой сумме внешних сил, распол-ых по одну сторону от сечения..
Что бы наглядно видеть места с наиб-им N строится эпюра, это график показ-ий изм-ие того или иного фактора по длине бруса.
5) По усилию нельзя судить о прочности стержня.
Определение нормальных напряжений (σ) в поперечном сечении
Рассм-им растянутый стержень:
В сечении выделим элем-ую площадку dA, по ней действ-щее напряжение σ:
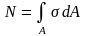
Для нахождения напряжения ур-ий статики не достаточно, необх знать з-н распред напряжения в поперечном сечении.
Прибегнем к эксперименту на пов-ть образца нанесём ряд ║ линий, увидим, что после деф поперечные линии не искривились и все точки по высоте сечения переместились на одну и туже вел-ну. Можно предположить, что такая же картина происх и в нутрии тела, т.е. плоские попер сечения до деф остаются плоскими и после деф. Эта гипотеза плоских сечений или гипотеза Бернулли. Из этой гипотезы следует, что и нормальное напряжение по высоте сечения остаются постоянными.
σ = const
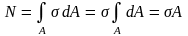
 - нормальное
напряжение при прод-ом растяж-сжатии
- нормальное
напряжение при прод-ом растяж-сжатии
При расчете напряжения также используется принцип Сен-Венона: « Напряж состоян тела на достаточно удален от облости действия нагрузок очень мало зависит от детального способа прилож этих нагрузок

