§ 2. Основные методы интегрирования
Основные методы интегрирования – это: а) метод разложения; б) метод подстановки; в) метод интегрирования по частям. Рассмотрим эти методы.
1. Метод разложения. Метод заключается в том, что подынтегральную функцию представляют в виде суммы таких функций, интегралы от которых можно взять по таблице.
Поясним этот метод примерами.
Пример 1.
.
Пример 2.
.
2.
Метод подстановки. Пусть
на промежутке
.
Если
– дифференцируемая на некотором
интервале функция, а её значения
,
то согласно замечанию 3 §1 имеем
. (1)
Формула (1) и является сутью метода подстановки. Частным случаем этого метода является метод подведения под знак дифференциала, когда явно переменную не вводят. Продемонстрируем метод примерами.
Пример 3.
.
В частности,
.
Пример 4.
.
Преобразуем квадратный трёхчлен в знаменателе следующим образом:
,
где
,
– дискриминант.
а) Пусть Д<0, тогда
.
б) Пусть Д>0, тогда
.
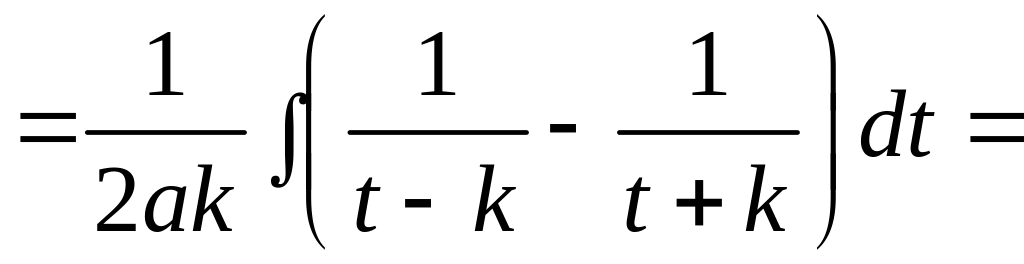
Упражнение.
Вычислить
интеграл
.
Пример 5.
.
3. Интегрирования
по частям. Пусть функции
и
– дифференцируемые на некотором
промежутке
и интеграл
– существуют. Тогда существует и интеграл
. (2)
Для доказательства
(2) достаточно убедиться, что дифференциал
правой части равен подынтегральному
выражению левой части. Действительно,
.
Что и требовалось доказать.
Формула (2) называется формулой интегрирования по частям.
Формула применяется для вычисления интегралов вида:
и некоторых других.
Пример 6.
.
Пример 7.
.
.
Пример 8.
.
Упражнение.
.
Доказать.
Пример 9.
или
. (1)
Формула (1) называется
рекуррентной. Она сводит вычисление
интеграла
к вычислению интеграла
.
Например,
.
Согласно формуле (1),
.
Зная теперь
,
вычислим
и
так далее.
Пример 10.
.
Подстановкой
сводится к интегралу примера 9.