Глава 7. Неопределённый интеграл

§ 1. Первообразная и неопределённый интеграл. Таблица интегралов

В главе 5 мы для заданной функции находили её производную . Операцию нахождения производной называли дифференцированием. Не менее важна обратная операция – по заданной производной найти (восстановить) функцию . Например, согласно второму закону Ньютона , где – время, – сила, действующая на точку. Эта сила обычно известна, а нужно найти закон движения точки под действием этой силы. То есть по известной производной найти функцию .

Операция, обратная дифференцированию, называется интегрирова-нием.

Определение 1. Пусть функция определена на некотором конечном или бесконечном промежутке . Функция , определённая и дифференцируемая на этом же промежутке , называется первообразной функции , если .

Например, . Очевидно, – первообразная этой функции, поскольку

.

Замечание 1. Часто вводят понятие нестрогой первообразной функции . В этом случае не требуют дифференцируемости, но требуют непрерывности функции и равенства во всех точках , исключая, быть может, счётное множество точек. Очевидно, всякая первообразная является нестрогой первообразной, но не наоборот.

Если – первообразная функции , то и , где , – также первообразная, так как . С другой стороны, если и – первообразные функции , то , или (смотри теорему 1 §3 глава 5). То есть произвольную первообразную можно записать в виде , где – некоторая конкретная первообразная. Другими словами, – множество всех первообразных функций на некотором промежутке .

Определение 2. Множество всех первообразных функции , определённых на некотором промежутке , называют неопределённым интегралом функции . Обозначают

. (1)

Выражение называют подынтегральным, а – подынтегральной функцией.

Равенство (1) означает, что или , то есть подынтегральное выражение – это дифференциал произвольной первообразной.

Возникает вопрос – каждая ли функция имеет первообразную? Ответ – нет. Например, функция не может иметь первообразную на интервале, содержащем точку , так как производная функция не может иметь точек разрыва 1-го рода (см. следствие теоремы 2 §3 гл. 6).

Позже докажем, что любая непрерывная на промежутке функция имеет на нём первообразную. А поскольку всякая элементарная функция непрерывна в области определения, то любая элементарная функция на любом промежутке непрерывности имеет первообразную.

Заметим, что непрерывность – достаточное условие существования первообразной, но не является необходимым условием. Например, функция разрывна в точке , но является первообразной этой функции на любом интервале числовой оси (убедиться в этом самостоятельно).

Замечание 2. Функция является нестрогой первообразной функции на любом интервале числовой оси, так как .

Операции дифференцирования и интегрирования – взаимно- обратные, то есть если , то . Поскольку , где – тождественный оператор, то имеем следующие свойства:

. (2)

Оператор интегрирования обладает свойством линейности, то есть

, (3)

если функции и имеют первообразные на одном и том же промежутке . Чтобы доказать (3), достаточно убедиться в том, что дифференциал правой части (3) равен подынтегральному выражению левой части этого равенства.

Действительно,  . Что и требовалось доказать.

Замечание 3. В равенстве (1) предполагалось, что – независимая переменная функций и . Однако равенство (1) справедливо и в случае, когда – дифференцируемая функция переменной  .То есть из (1) следует, что

. (4)

Действительно, используя инвариантность формы первого дифференциала, имеем . Что и требовалось доказать.

Таблицу неопределённых интегралов от основных элементарных функций получим из таблицы производных (дифференциалов).

1. .

2. .

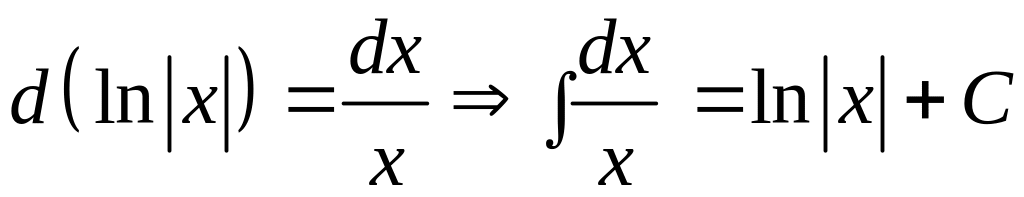3. .

4. .

5. .

6. .

7. .

8. .

9.

.

10. .

11. .

12. (проверить дифференцированием).

Согласно замечанию 3 все табличные интегралы справедливы и в том случае, если – дифференцируемая функция аргумента . В частности, используя 8-й табличный интеграл, получим

.

Аналогично из 9-го интеграла таблицы получим

.

Замечание 4. Первый интеграл таблицы справедлив и для отрицательных при некоторых значениях . Например, при имеем . Здесь – первообразная функции на любом интервале числовой оси. При имеем , не является первообразной функции на интервале, содержащем точку , так как не является на нём дифференцируемой функций. В то же время является нестрогой первообразной. При имеем . Функция не является даже нестрогой первообразной для функции на интервале, содержащем точку , так как не является на нём непрерывной. На любом интервале, не содержащем точку , она является первообразной.

Аналогичное замечание можно сделать и для второго интеграла таблицы и для некоторых других.

Замечание 5. Определения 1 и 2 справедливы и для векторной функции действительного аргумента . Например, для функции первообразной будет . В частности, для комплексной функции скалярного аргумента первообразной будет .