
- •§10. План исследования функции и построение графика
- •§ 11. Вектор-функция скалярного аргумента. Основные понятия
- •§ 12. Понятие кривой, касательная к кривой, длина кривой
- •§13. Кривизна и кручение кривой
- •Глава 7. Неопределённый интеграл
- •§ 1. Первообразная и неопределённый интеграл. Таблица интегралов
- •§ 2. Основные методы интегрирования
§13. Кривизна и кручение кривой
М
Пусть
![]() – гладкая
кривая,
– единичный
вектор касательной к кривой
в точке
– гладкая
кривая,
– единичный
вектор касательной к кривой
в точке
![]() ,
а
,
а
![]() – в точке
– в точке
![]() ,
,
![]() – приращение
вектора
на дуге
– приращение
вектора
на дуге
![]() ,
длина которой
,
длина которой
![]() ,
а угол между векторами
и
равен
,
а угол между векторами
и
равен
![]() .
Его называют углом смежности (см. рис.).
.
Его называют углом смежности (см. рис.).
Определение 1. Кривизной кривой в точке называют предел отношения угла смежности к длине дуги , то есть
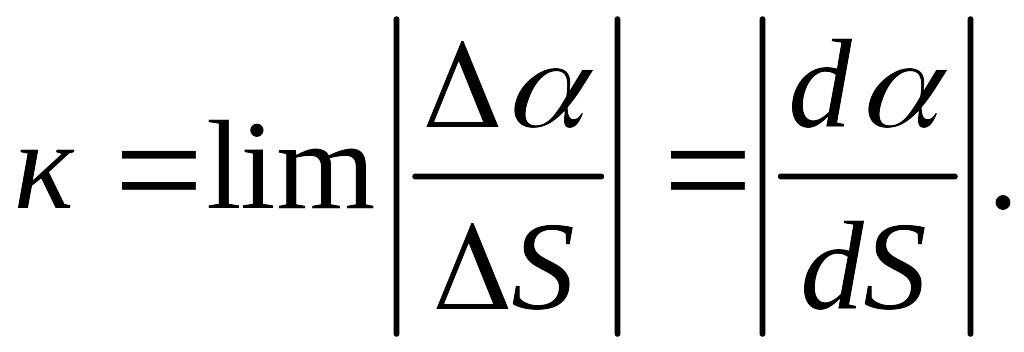 (1)
(1)
Обратную величину
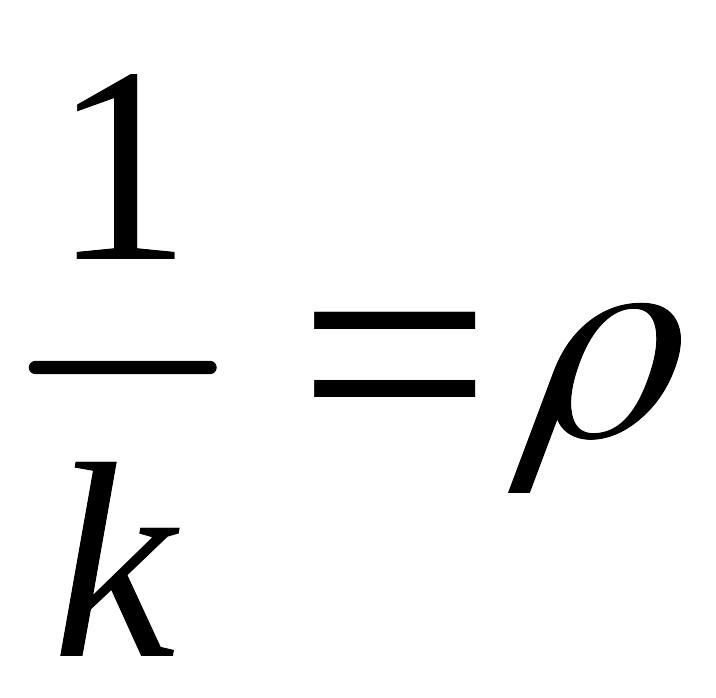 называют радиусом кривизны кривой в
точке
.
называют радиусом кривизны кривой в
точке
.
Из рисунка видно, что
 при
при
![]() (2)
(2)
Тогда из (1) с учётом (2) получим
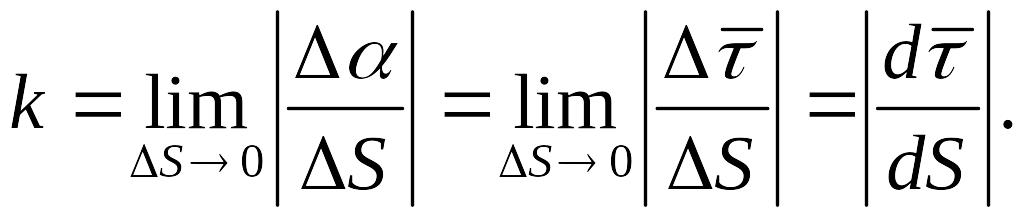 (
)
(
)
Лемма. Производная единичного вектора перпендикулярна к самому вектору.
Доказательство.
Пусть
![]() – единичный
вектор. Тогда
– единичный
вектор. Тогда
![]() .
Дифференцируя это тождество, найдём
.
Дифференцируя это тождество, найдём
 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Продифференцируем
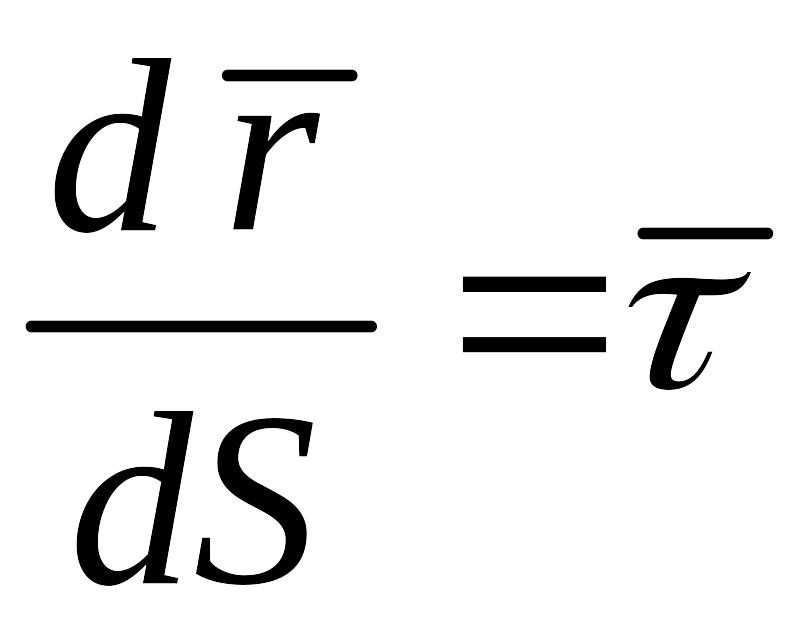 (см. (15) §12)
ещё раз
(см. (15) §12)
ещё раз
 (3)
(3)
Здесь
![]() – кривизна
кривой, а
– кривизна
кривой, а
![]() – единичный
вектор. Согласно лемме он перпендикулярен
единичному вектору касательной
.
Его называют главной нормалью кривой
в точке
.
Единичный вектор
– единичный
вектор. Согласно лемме он перпендикулярен
единичному вектору касательной
.
Его называют главной нормалью кривой
в точке
.
Единичный вектор
![]() называют
бинормалью,
а правую ортонормированную тройку
векторов
называют
бинормалью,
а правую ортонормированную тройку
векторов
![]() и
и
![]() репером
Френе.
репером
Френе.
Если
![]() – скорость
точки, то
– скорость
точки, то
![]() – её
ускорение. По правилу дифференцирования
сложной функции найдём
– её
ускорение. По правилу дифференцирования
сложной функции найдём
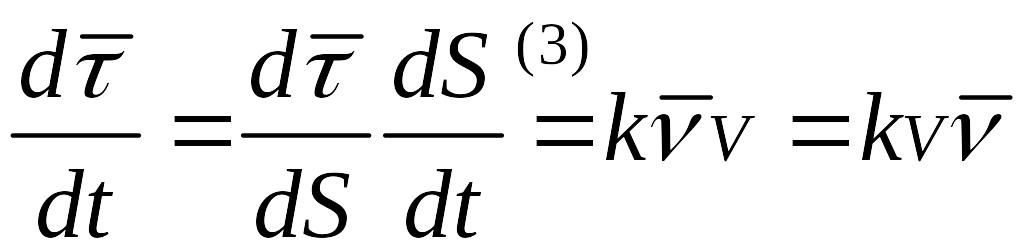 . (4)
. (4)
 . (5)
. (5)
Получили разложение
ускорения на касательное
 и нормальное
и нормальное
 .
.
Предполагая
существование нужных производных,
выразим кривизну
кривой через
производные векторной функции
.
Поскольку векторы
и
![]() коллинеарные, то угол смежности между
векторами
и
коллинеарные, то угол смежности между
векторами
и
![]() будет равен углу между векторами
будет равен углу между векторами
![]() и
и
![]() .
.
![]() . (6)
. (6)
Поскольку
![]() и
и
![]() при
при
![]()
![]()
(см. ( ) §12), то из (1) получим


Итак,  (7)
(7)
Плоскость, проходящую
через точку
![]() на кривой
,
нормалью которой служит бинормаль
на кривой
,
нормалью которой служит бинормаль
![]() ,
называют соприкасающейся
плоскостью.
,
называют соприкасающейся
плоскостью.
Так как
![]() ,
а
,
а
![]() (см. (5)), то векторы
(см. (5)), то векторы
![]() перпендикулярны бинормали
перпендикулярны бинормали ![]() ,
следовательно, лежат в соприкасающейся
плоскости.
,
следовательно, лежат в соприкасающейся
плоскости.
Пусть
– произвольная
точка соприкасающейся плоскости. Тогда
векторы
![]() и
и
![]() – компланарные
и их смешанное произведение равно нулю.
– компланарные
и их смешанное произведение равно нулю.
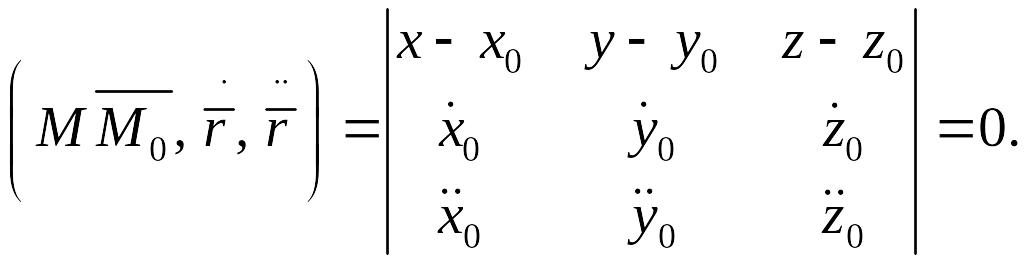 (8)
(8)
Уравнение (8) – уравнение соприкасающейся плоскости.
Пусть
![]() – угол
между двумя соприкасающимися плоскостями,
проходящими через точки
и
на кривой
,
а
–
длина дуги
– угол
между двумя соприкасающимися плоскостями,
проходящими через точки
и
на кривой
,
а
–
длина дуги
![]() .
.
Определение 2. Предел отношения угла к длине дуги называют абсолютным кручением кривой в точке
 (9)
(9)
Угол
между соприкасающимися плоскостями в
точках
и
равен углу между нормалями
и
![]() в этих точках. Сравнивая определения
кривизны и абсолютного кручения, видим,
что они ничем не отличаются, углы только
берутся не между касательными, а между
бинормалями. Поэтому аналогично получим
формулу
в этих точках. Сравнивая определения
кривизны и абсолютного кручения, видим,
что они ничем не отличаются, углы только
берутся не между касательными, а между
бинормалями. Поэтому аналогично получим
формулу
 (
(![]() )
)
(см. вывод формулы ( )).
Согласно лемме
![]() и
– ортогональны.
Поэтому можно записать
и
– ортогональны.
Поэтому можно записать
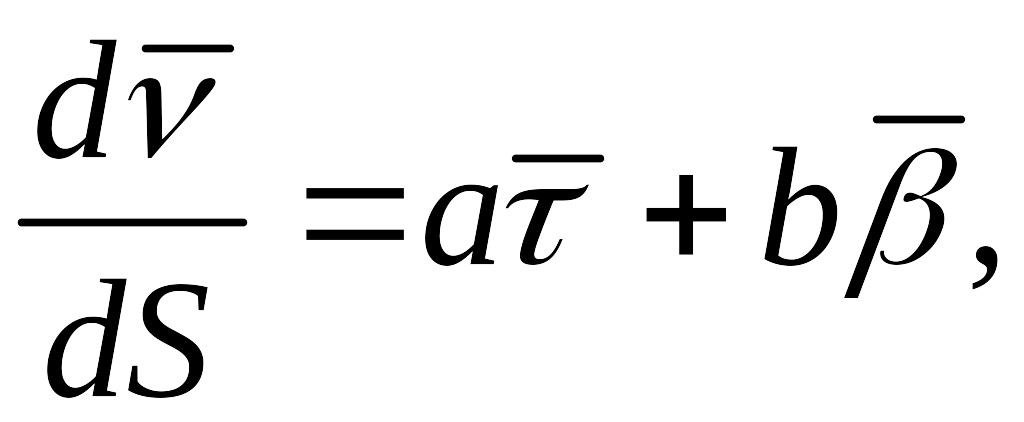 (10)
(10)
где
![]() и
и
![]() – неизвестные
коэффициенты разложения.
– неизвестные
коэффициенты разложения.
Дифференцируя
тождество
![]() ,
получим
,
получим

Учитывая это, перепишем (10) в виде
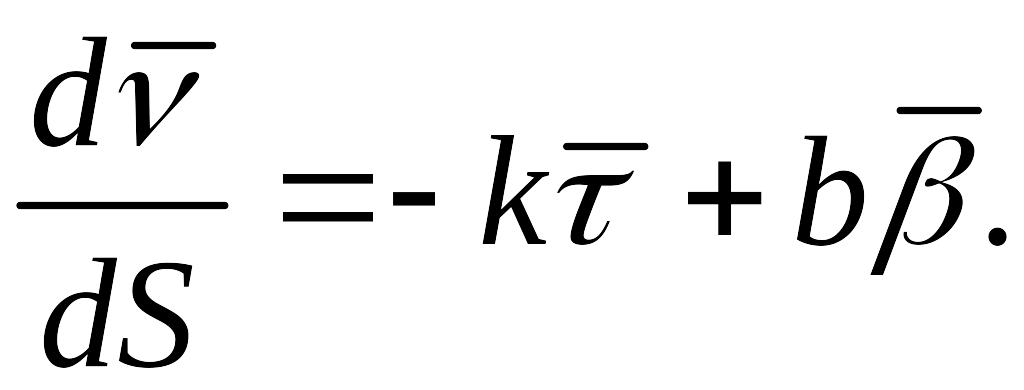 (
(![]() )
)
Продифференцируем другое тождество . Получим
 . (11)
. (11)
Из (11) получим
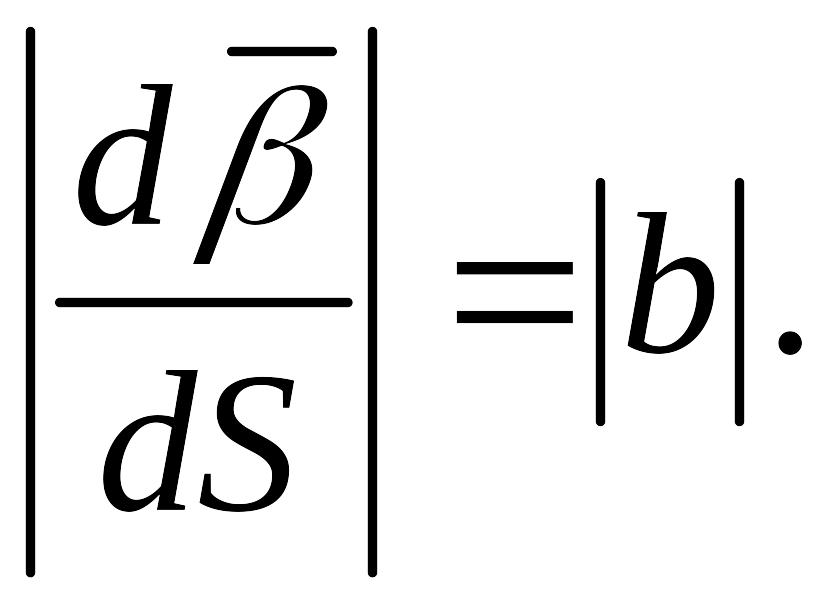 (12)
(12)
Сравнивая (12) с
(
),
найдём
![]() .
Назовём
.
Назовём
![]() кручением кривой в точке
кручением кривой в точке
![]() (в отличие от абсолютного кручения
(в отличие от абсолютного кручения
![]() может быть и отрицательным). Перепишем
формулу (
)
и (11)
может быть и отрицательным). Перепишем
формулу (
)
и (11)
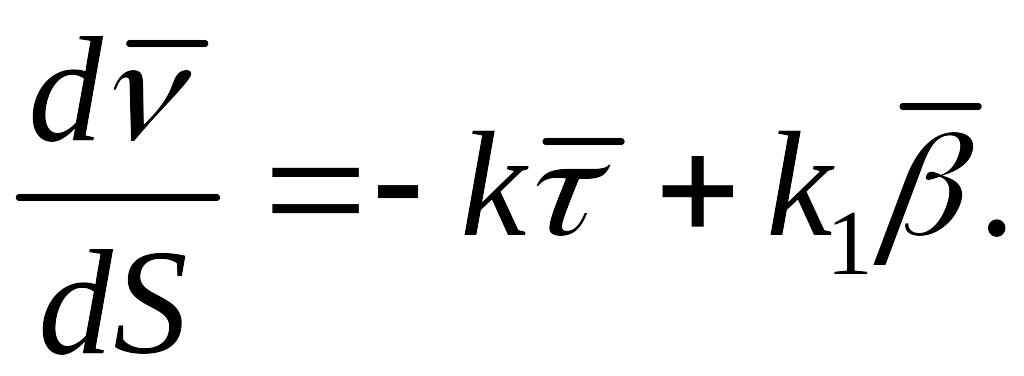 (
(![]() )
)
 (
(![]() )
)
Дифференцируя (3), получим
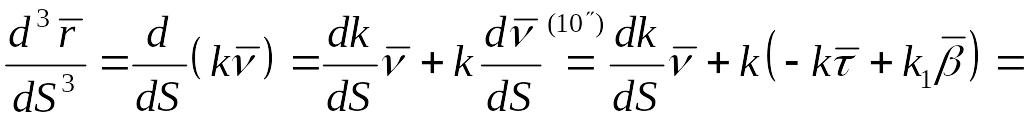
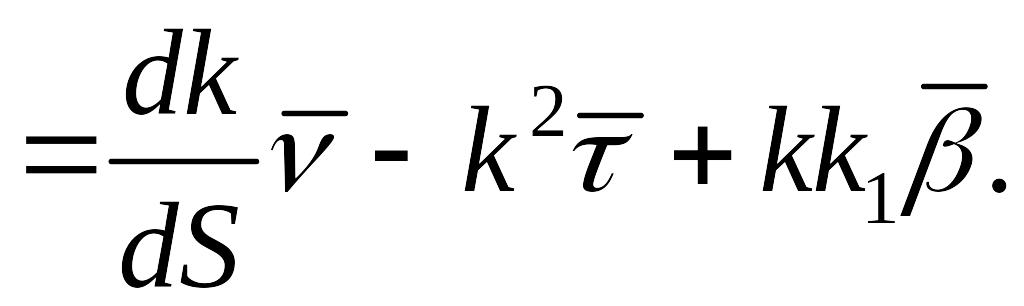 (13)
(13)
Выпишем полученные формулы.
 (см. (15) §12),
(см. (15) §12),
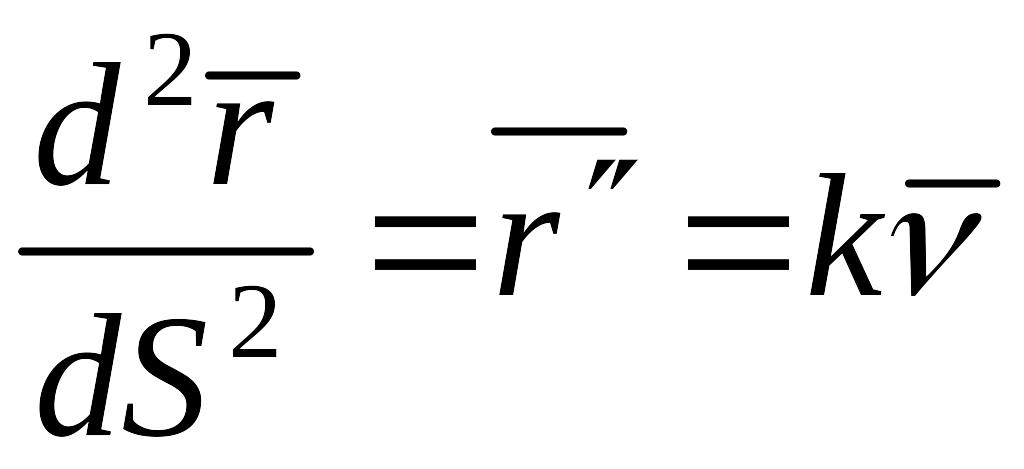 (3),
(3),
 (13).
(13).
Найдём векторное произведение
![]() (14)
(14)
Найдём смешанное произведение
![]() .
.

 . (15)
. (15)
Зная векторное
представление кривой
![]() ,
по формуле (15) можно вычислить кривизну
.
,
по формуле (15) можно вычислить кривизну
.
Замечание. Формула
(15) верна и в том случае, если производные
берутся не по длине кривой
![]() ,
и по параметру
.
То есть формулу (15) можно записать
,
и по параметру
.
То есть формулу (15) можно записать
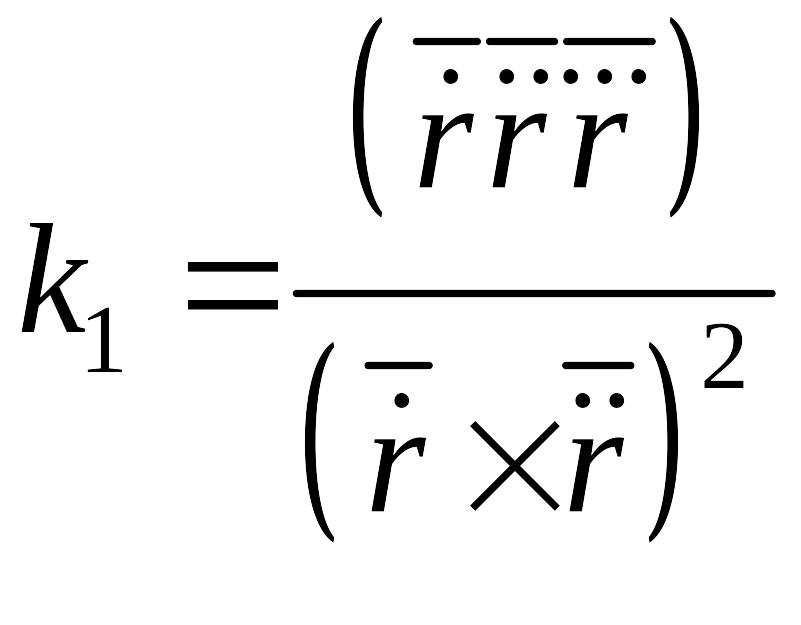 . (
. (![]() )
)
Пример. Найти
кривизну и кручение винтовой линии
![]() ,
,
![]() .
.
Решение. Найдём производную радиус-вектора
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
Согласно ( ),
 .
.
Согласно (7),
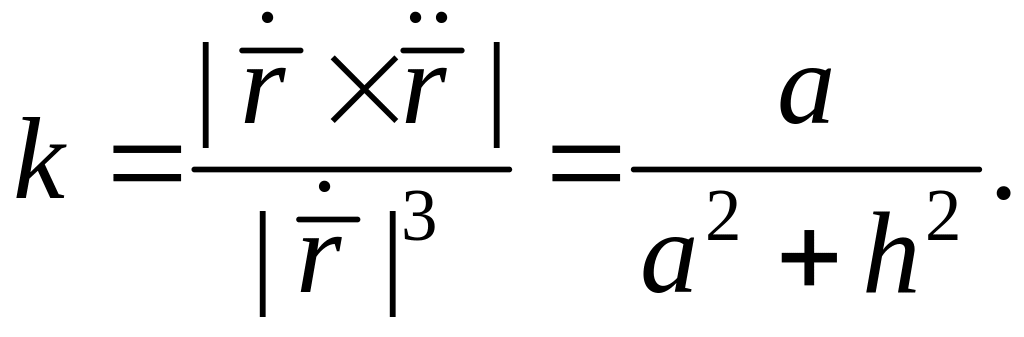
Как видно, винтовая линия имеет постоянное кручение и кривизну.
