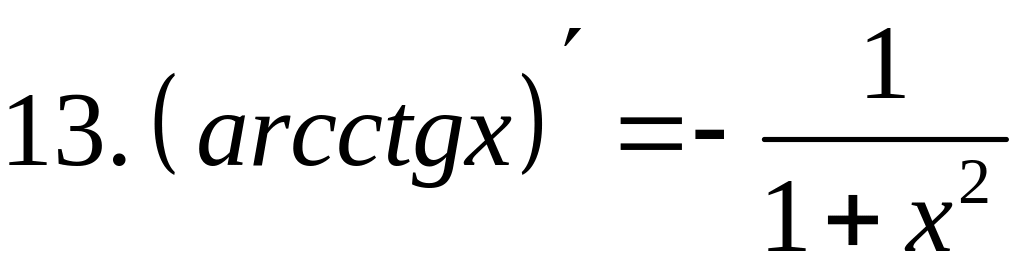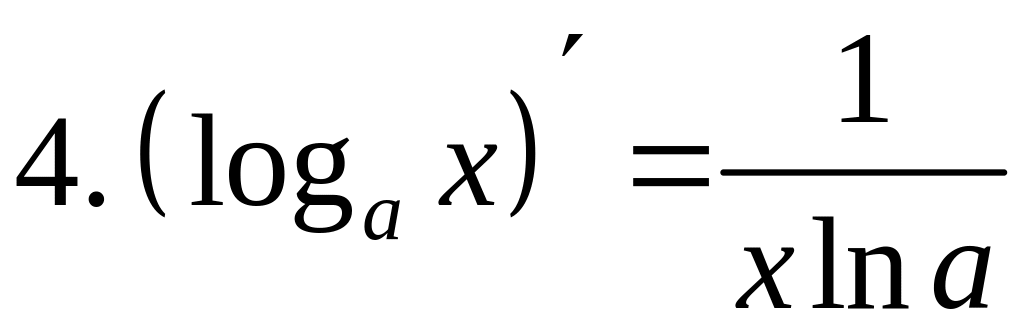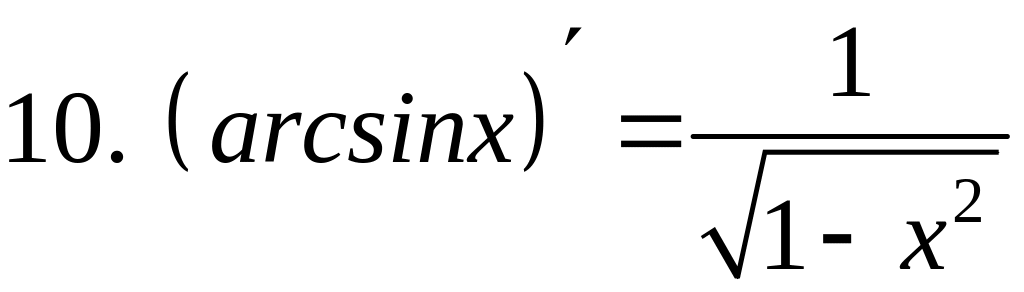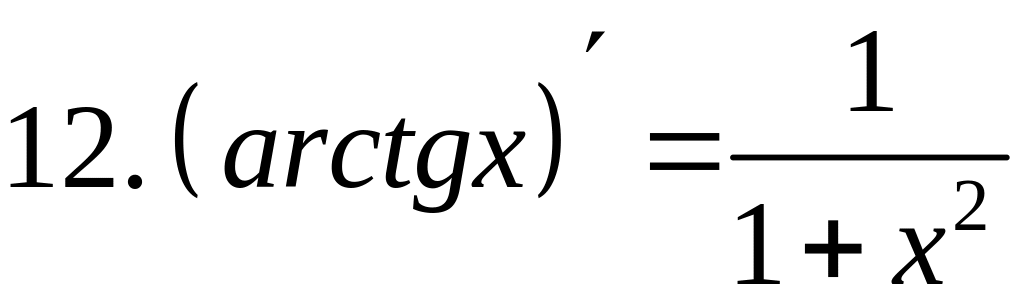- •2) Логарифмическая функция
- •3) Степенная функция
- •4) Обратные тригонометрические функции
- •Глава 5. Дифференциальное исчисление функции одной переменной
- •§1. Понятие производной функции
- •§2. Геометрический и физический смысл производной
- •§3. Дифференцируемость функции. Дифференциал
- •§4. Правила вычисления производной и дифференциала
- •§5. Производная обратной и сложной функций. Таблица производных
- •§6. Производная высшего порядка. Формула Лейбница
- •§7. Производные высших порядков от сложной, неявной и параметрически заданной функций
- •§8. Инвариантность формы первого дифференциала. Дифференциалы высших порядков
§5. Производная обратной и сложной функций. Таблица производных
Теорема 1. Пусть
функция
определена, непрерывна и строго монотонна
в окрестности точки
и пусть ее производная в точке
существует и отлична от нуля,
![]() Тогда обратная функция
Тогда обратная функция
![]() также
имеет производную в точке
также
имеет производную в точке
![]() ,
причем
,
причем
 . (1)
. (1)
Доказательство.
Существование
обратной
функции
![]() ,
непрерывной и строго монотонной в
окрестности точки
гарантирует теорема 3 §11 главы 4. Поэтому
условия
,
непрерывной и строго монотонной в
окрестности точки
гарантирует теорема 3 §11 главы 4. Поэтому
условия
![]() и
и
![]()
эквивалентны и
так как обе функции строго монотонны,
то
![]() и
и
![]() .
Запишем тождество
.
Запишем тождество
 .
.
![]()
Переходя к пределу, имеем

Так как предел правой части существует, то существует и предел левой части, то есть

Теорема доказана.
Равенство (1) можно записать в симметричной форме
 .
.
Индекс показывает, по какой переменной берется производная.
Пример 1.
![]() Найти
Найти
![]()
Решение.
![]() .
.
Согласно имеем
 .
.
Итак,
 .
.
Пример 2.
![]()
![]()
![]()
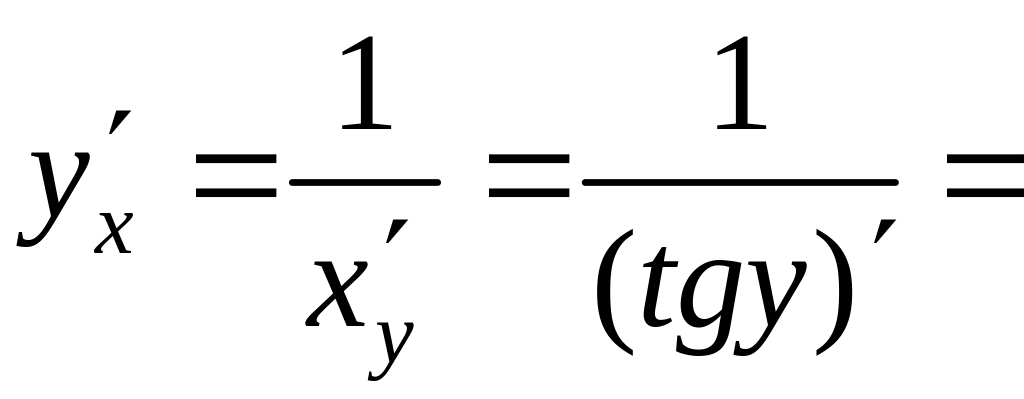
![]()
 .
.
Итак,
 .
.
Упражнение. Доказать, что  ,
,
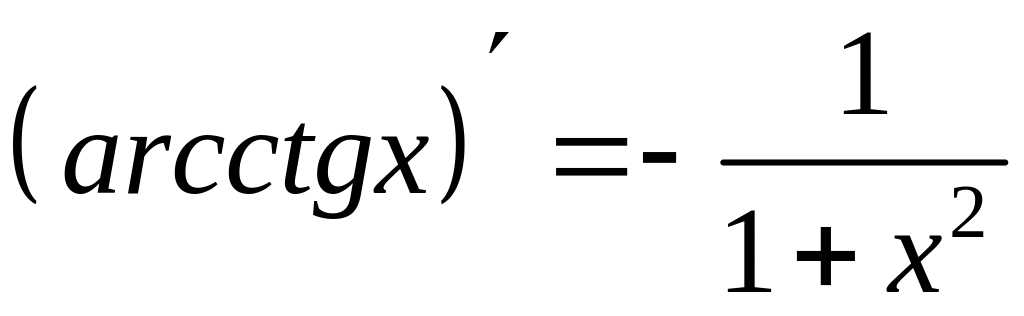 .
.
Если
![]() ,
а
,
а
![]() ,
то суперпозицию этих функций называют
сложной функцией
,
то суперпозицию этих функций называют
сложной функцией
![]() .
.
Теорема 2. Если
![]() и
и
![]() существуют, где
существуют, где
![]() ,
то существует и производная сложной
функции
,
то существует и производная сложной
функции
![]() в точке
,
причем
в точке
,
причем
![]() .
. ![]()
Доказательство.
Так как
функции
и
![]() имеют производные в точках
и
соответственно, то и непрерывны в этих
точках (см. §7). Сложная функция
непрерывна в точке
(см. теорему 2 §8 гл. 4), поэтому при
имеют производные в точках
и
соответственно, то и непрерывны в этих
точках (см. §7). Сложная функция
непрерывна в точке
(см. теорему 2 §8 гл. 4), поэтому при
![]() .
Функция
.
Функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
поэтому
,
поэтому
![]()
(см. §3). 
 .
Итак,
.
Итак,
![]() .
. ![]()
Теорема доказана.
Пример 3. Найти
производную степенной функции
![]() .
.
Решение.
![]() ,
,
![]() – сложная функция. Воспользуемся
– сложная функция. Воспользуемся
![]() .
.
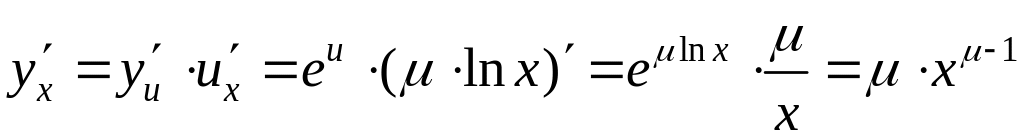 .
.
Итак,
![]()
Пример 4. ![]()
![]() сложная функция.
сложная функция.


Итак,

Пример 5. ![]() сложная функция.
сложная функция.
![]()

Замечание 1. Теорема 2 верна и для большего числа суперпозиций функций.
Пример 5. ![]()
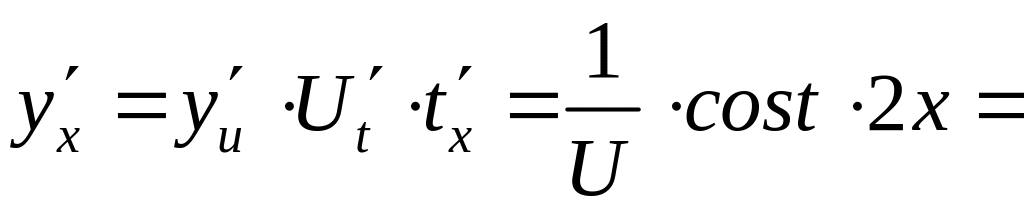

Сведем все вычисленные выше производные в таблицу (таблицу выучить наизусть).
Таблица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 2. Как видно из приведенных примеров, основные элементарные функции дифференцируемые. Из правил дифференцирования суммы, произведения, отношения, сложных функций следует, что любая элементарная функция имеет производную в области определения и является элементарной функцией в области определения.
§6. Производная высшего порядка. Формула Лейбница
Пусть функция
определена на интервале
![]() и в каждой точке этого интервала имеет
производную
.
Так как производная
является функцией, определённой на
интервале
,
то сама может иметь производную.
Производная от производной называется
второй производной, или производной
второго порядка. Обозначают её так:
и в каждой точке этого интервала имеет
производную
.
Так как производная
является функцией, определённой на
интервале
,
то сама может иметь производную.
Производная от производной называется
второй производной, или производной
второго порядка. Обозначают её так:
![]()
Аналогично можно
ввести третью и так далее производную.
n-я
производная – это производная от
![]() -й
производной
-й
производной
![]() .
.
Функция называется n-раз непрерывно дифференцируемой в точке x, если существует некоторая окрестность этой точки, в которой
![]() -я
производная непрерывна. Естественно,
что
-я
производная в этой точке – функция
дифференцируемая.
-я
производная непрерывна. Естественно,
что
-я
производная в этой точке – функция
дифференцируемая.
Пример 1.
![]() .
.
Очевидно
![]() (1)
(1)
Формулу можно доказать методом математической индукции.
В частности, если
![]() натуральное,
то
натуральное,
то
![]() !,
а
!,
а
![]() при
при
![]() .
.
Пример 2.
![]() ,
,
![]()
![]()
![]() (2)
(2)
![]()
Пример 3.
![]() ,
,
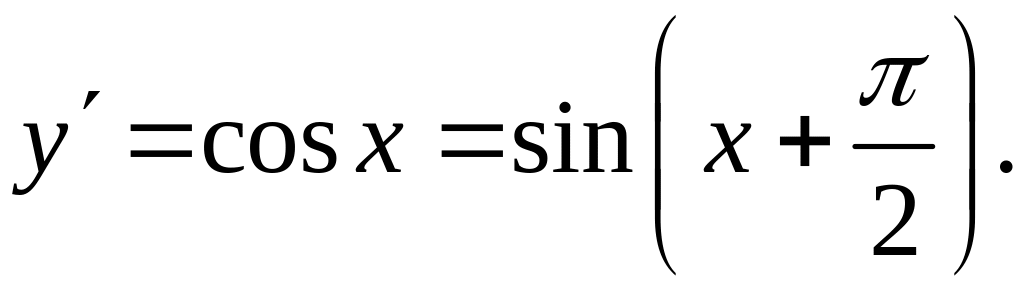
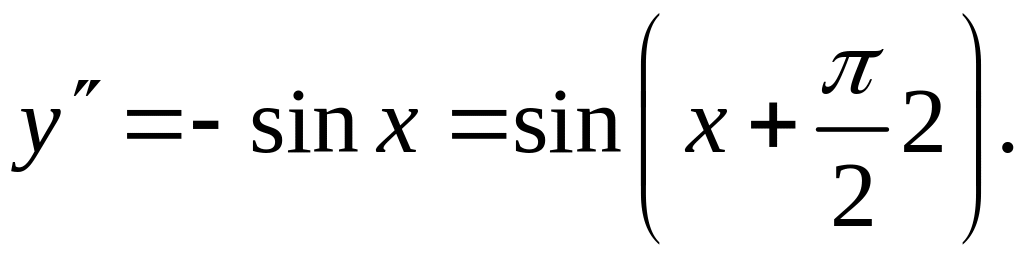
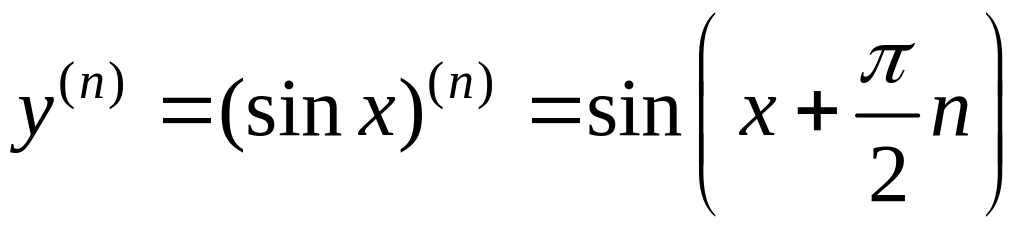 – гипотеза.
– гипотеза.

 .
.
Формула доказана методом математической индукции.
Упражнения. Доказать, что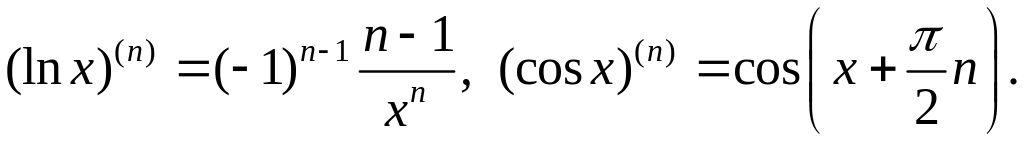
Очевидно, константу можно вынести за знак производной любого порядка, то есть
![]() .
.
Производная от суммы двух функций равна сумме производных, то есть
![]() ,
,
если последние существуют.
Найдём теперь -ю производную от произведения двух функций. Докажем, что
 ,
(3)
,
(3)
где
![]() Формула (3)
называется
формулой Лейбница.
Формула (3)
называется
формулой Лейбница.
Доказательство. Воспользуемся методом математической индукции, предварительно отметив, что
![]()
Проверим формулу
(3) при
![]() .
.
![]()
– формула
справедлива. Пусть (3) справедлива. Найдём
![]() -ю
производную.
-ю
производную.

(введём обозначение
![]() в первой сумме)
в первой сумме)

![]()

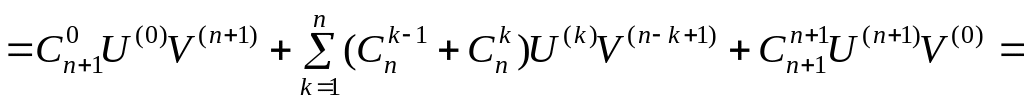
 .
.
Что и требовалось доказать.
Пример 4. Найти
![]() .
.
Решение. Воспользуемся формулой Лейбница.
![]() .
.