Поскольку
и
(см. §4 гл. 2), то по теореме о двух
милиционерах из (2) и (1) получим
Если
,
доказательство аналогично. Теорема
доказана.
2) Логарифмическая функция
Поскольку у=ах
– строго монотонна и непрерывна на
всей числовой оси, то, согласно теореме
3 §11, обратная функция
существует,
монотонна и непрерывна на всей числовой
оси. (Если переобозначить аргумент и
функцию, то получим данную функцию
).
3) Степенная функция
Ранее (см. пример
1 §7) мы доказали, что при
степенная функция непрерывна. Докажем,
что она непрерывна при любом действительном
.
Запишем степенную
функцию в виде
,
то есть в виде суперпозиции двух функций
и
.
Поскольку обе
функции (
и
)
непрерывны, то согласно теореме 2 §8
сложная функция
непрерывная в области определения.
4) Обратные тригонометрические функции
Ранее (см. пример
9 §7) доказано, что тригонометрические
функции
и
непрерывны на всей числовой оси. Поскольку
на отрезке
функция
строго монотонна, то, согласно теореме
3 §11, она имеет на этом отрезке обратную
функцию
,
строго монотонную и непрерывную.
Аналогично можно доказать, что 
непрерывная
функция.
Таким образом, мы доказали, что все основные элементарные функции непрерывны в своей области определения. А так как любая элементарная функция получается из основных пяти элементарных функций путем конечного числа арифметических операций и путем суперпозиций функций, то из теоремы 1, 2 §8 следует справедливость следующей теоремы.
Теорема. Всякая элементарная функция непрерывна в своей области определения.
Глава 5. Дифференциальное исчисление функции одной переменной
§1. Понятие производной функции
Пусть действительная
функция
определена
на интервале
и пусть
– любая точка этого интервала. Дадим
приращение аргументу
такое, что
и вычислим приращение функции
в точке
.
Определение. Если существует предел отношения приращения функции к приращению аргумента
,
(1)
то этот предел
называется производной функции
в точке
.
Обозначают производную так:
(Лагранж),
(Лейбниц),
(Ньютон).
Процесс нахождения
производной называют дифференцированием
функции. Оператор
называют дифференциальным.
Если в (1) берется
левый или правый пределы, то и производная
называется левой или правой. Обозначают
и
соответственно. Очевидно, если существует
производная (1), то существуют левая и
правая производные, причем
=
.
Наоборот, если существуют
,
и
=
,
то существует и производная (1).
Если производная
существует во всех точках интервала
,
то мы имеем производную функцию
,
заданную на интервале
.
Если еще вдобавок существует
и
,
то имеем производную функцию
,
заданную на отрезке
.
(В общем случае областью определения
функции
является множество точек
,
в которых она существует).
Пример 1.
Найти производную функции
,
.
Решение. Дадим приращение аргументу и найдем приращение функции в произвольной точке .
.
Воспользуемся (1).
.
(воспользовались
первым замечательным пределом и
непрерывностью функции
).
Итак,
для любого
.
Упражнение.
Доказать,
что
Пример 2. Найти
производную функции
в точке
.
Решение. Найдем
левую и правую производные в точке
.
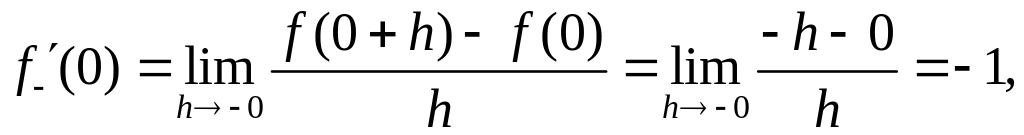
Итак,
,
следовательно, функция не имеет
производной в точке
.
Очевидно,
Заметим, что функция
всюду непрерывная, а ее производная
функция разрывная.
Пример 3.
Найти .
Решение. Найдем сначала производную в точке .
Пусть теперь
Итак,
Заметим, что
не существует, но
,
то есть функция
терпит разрыв в точке
.
Это точка разрыва второго рода.
Теорема. Если функция имеет производную в точке , то она непрерывна в этой точке.
Доказательство. Из существования предела (1) следует
,
где
бесконечно
малая в точке х.
Тогда
при
Так как бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывная. Теорема доказана.
Следствие. Если
функция определена в некоторой окрестности
точки
,
но в точке
терпит разрыв, то
не существует. Доказательство от
противного.
Пример 4. Найти
производную функции
Решение. Очевидно,
функция разрывная всюду, исключая точки
и
.
В них она непрерывная, поэтому, согласно
следствию, она может иметь производную
только в этих точках. Пусть
–рациональное, тогда
Пусть теперь – иррациональное, тогда
,
Итак, данная функция имеет производную только в одной точке , причем .
Пример 5.
то
есть разрывная функция имеет всюду
производную. Где ошибка?
Замечание. Иногда рассматривают частный случай производной, так называемую симметрическую производную, или производную
Шварца. Она определяется формулой
.
(2)
Очевидно, если существует обычная производная (1), то существует и равная ей производная Шварца. Однако, если обычная производная не существует, то симметрическая производная может существовать. Например, производная в нуле функции примера 2 не существует, а производная Шварца существует и равна нулю. Действительно,
.