Свойства аффинного преобразования:

1. любое аффинное преобразование может быть представлен как последовательность операции из числа простейших: сдвиг, растяжение, сжатие, поворот.

2. сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Трехмерные аффинные преобразования.

Запишем их в виде формул:

X=Ax+By+Cz+D

Y=Ex+Fy+Gz+H

Z=Ix+Jy+Kz+l

где A…L=const.

В матричной форме это выражение представляется в следующем виде:

Для трехмерного пространства любое аффинное преобразование также может быть представлено последовательностью простейших операций. Рассмотрим эти операции:

1. сдвиг осей координат на dx, dy, dz по аналогии с двухмерном пространстве:

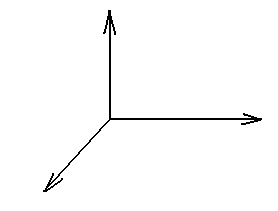
2. растяжение, сжатие(k_x,k_y,k_z):

X=x/k_x

Y=y/k_y

Z=z/k_z

3)поворот, подразделено на 3 операции:

а) поворот вокруг оси x

б) поворот оси y

в) поворот вокруг оси z

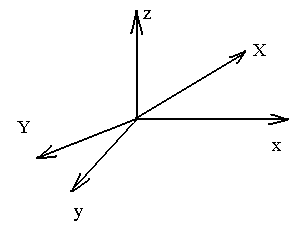
Преобразование объектов.

Преобразование объектов можно описать так. Пусть любая точка, которая принадлежит определенному объекту, имеет координаты k₁,k₂…k_n в n-мерной системе координат. Тогда преобразование объекта можно определить как изменение положения точек объекта. Новое положение точки отвечает новым значениям координат m₁,m₂…m_N.

Соотношение между новыми и старыми координатами для всех точек объекта:

(m₁,m₂…m_N)=F(k₁,k₂…k_n)

и будет определять образование объекта.

Классифицировать преобразование объекта можно по типу функции преобразования и по типу систем координат. Афинные преобразования на плоскости и в трехмерном пространстве аналогичны афинным преобразованиям координат. Преобразование объектов и преобразование координат связаны между собой. Движение объектов можно рассматривать как движение в обратном направлении соответствующей системы координат. Такая относительность для объектов отображения и систем координат дает дополнительные возможности для моделирования и визуализации пространственных объектов. С каждым объектом может быть связано собственная локальная система координат, так и единое для нескольких объектов. Данное свойство широко используется для моделирования подвижных объектов.

Рассмотрим пример комбинированного подхода. Пусть необходимо получить функцию расчета координат для поворота вокруг точки с произвольным центром.

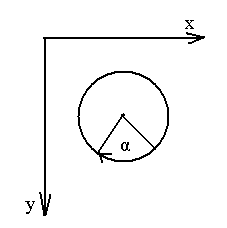
X=x-dx

Y=y-dy

1. X=x-x₀

Y=y-y₀

2. X=(x-x₀) cosα- (y-y₀)sinα

Y=(x-x₀) sinα- (y-y₀)cosα

3. X=((x-x₀) cosα- (y-y₀)sinα)+ x₀

Y=((x-x₀) sinα- (y-y₀)cosα)+ y₀

1 шаг. Сдвиг системы координат к центру, вокруг которого будет производиться вращение.

2 шаг. Вращение объекта.

3 щаг. Сдвиг системы координат.

Проекции

В настоящее время наиболее распространены отображения, которые синтезируют изображения на плоскости. Следовательно, при использовании любых графических устройств обычно используют проекции. Проекция задает способ отображения объекта на графическом устройстве.