5. Методы организации данных

5.1. Структуры данных и алгоритмы в ЭИС

Методы хранения данных в памяти компьютера обычно предполагают раздельное хранение значений каждой СЕИ (записи). Множество записей образуют массив или файл. Термин «массив» обычно относят к оперативной памяти, «файл» - к внешней. Как правило, файл содержит записи, принадлежащие к одной СЕИ, хотя в общем случае это не обязательно.

Организация данных понимается как относительно устойчивый порядок расположения записей данных в памяти компьютера и способ обеспечения взаимосвязи между записями.

Организация данных может быть линейной и нелинейной. При линейной организации данных каждая запись (кроме первой и последней) связана с одной предыдущей и одной последующей. При нелинейной организации количество предыдущих и последующих записей может быть произвольным.

Линейные методы различаются только способами указания предыдущей и последней записей по отношению к данной. В основном применяется последовательная организация данных, соответствующая понятию «массив» («файл»). Записи располагаются в памяти строго одна за другой, без промежутков, в той последовательности, в которой они обрабатываются.

Записи делятся на записи фиксированной, переменной и неопределенной длины. Записи переменной и неопределенной длины занимают меньший объем памяти, но обрабатываются медленнее.

В структуре записей выделяется один или несколько ключевых атрибутов, по значениям которых происходит доступ к значениям остальных атрибутов той или иной записи. Состав ключевых атрибутов необязательно соответствует первичному ключу.

Будем считать, что последовательный массив состоит из М записей фиксированной длины, в каждой из которых выделен только один ключевой атрибут P(i), где i - номер записи. Записи могут быть упорядоченными или неупорядоченными по значениям ключевого атрибута (ключа), имя которого одинаково во всех записях. Часто требуется упорядоченность записей по нескольким именам ключевых атрибутов. В этом случае среди атрибутов устанавливается старшинство. Условия упорядоченности записей имеют вид:

p(i)  p(i+1) - упорядочение по возрастанию,

p(i)  p(i+1) - упорядочение по убыванию.

Основные алгоритмы обработки данных сводятся к формированию, поиску, корректировке и последовательной обработке данных.

Данные обычно возникают в неупорядоченной форме. Перед обработкой их целесообразно упорядочить по значениям ключей - отсортировать. Это повышает эффективность обработки и облегчает восприятие человеком. Будем далее считать все массивы упорядоченными по возрастанию значений одного (ключевого) атрибута.

Естественная характеристика эффективности любого алгоритма - время его выполнения в зависимости от ряда параметров хранимой информации. Поэтому для каждого метода организации данных анализируют следующие величины:

1) время формирования данных, т.е. время создания в памяти компьютера так или иначе упорядоченного представления данных;

2) время поиска данных, обычно это поиск по совпадению - «найти записи, у которых значение ключевого атрибута равно заранее заданной величине q»;

3) время корректировки данных - обычно учитывается включение или исключение одной записи;

4) объем дополнительной памяти, расходуемой под служебную информацию (например, для хранения адресов связи).

Поскольку время - параметр не объективный (быстродействие компьютера, язык и стиль программирования влияют на время решения задачи), методы организации данных анализируют по количеству элементарных операций, в частности, операций сравнения, необходимых для реализации того или иного алгоритма.

Кроме того, при анализе алгоритмов принимают ряд допущений:

- распределение значений ключевых атрибутов в массиве из М записей равномерное,

- значение q при поиске выбрано случайно, это значит, что поиск может закончиться на любой записи массива с равной вероятностью (1/М),

- положение включаемой или исключаемой записи при корректировке, определяется теми же вероятностями, что при поиске.

Минимальное число сравнений при упорядочении последовательного файла определяется числом перестановок его элементов М!, т.е. все его состояния равновозможны. Процедура упорядочения состоит из серии сравнений значений ключевых атрибутов и тех или иных перестановок записей по результатам сравнения. Число сравнений (вопросов с возможными ответами “да - нет”) для упорядочения массива из М записей составляет

C = log₂M!

После преобразований по формуле Стирлинга получим

C=M(log₂M-1,43)

или C  Mlog₂ M

Поиск - процедура выделения из некоторого множества записей определенного подмножества, записи которого удовлетворяют поставленному условию. Условие поиска часто называют запросом на поиск. Простейшее условие - поиск по совпадению.

Базовый метод доступа к массиву - ступенчатый поиск. Метод предполагает упорядоченность обрабатываемых записей.

1 вариант - одноступенчатый (последовательный) поиск. Значение q последовательно сравнивается с ключами 1-й, 2-й и т.д. записей до момента совпадения (или пока q не станет больше p(i)). Поиск может закончиться с равной вероятностью 1/М на любой записи, поэтому

C=(M+1)/2 или C  M

2 вариант - двухступенчатый поиск. Задается константа d1 - шаг поиска. На первой ступени значение q сравнивается последовательно с p(1), p(1+d1), p(1+2d1), ..., p(1+kd1) до тех пор, пока не будет впервые достигнуто неравенство p(1+md1)>q. На второй ступени q последовательно сравнивается со всеми ключами, которые имеют номер 1+(m-1)d1 и больше до тех пор, пока в процессе сравнений не будет достигнут ключ, больший, чем q. Извлеченные при этом записи образуют результат поиска.

Среднее число сравнений здесь

Параметр d1 выбирается так, чтобы значение С было минимальным. Вычислив первую производную и приравняв ее к нулю, получим .

Аналогично анализируется многоступенчатый поиск.

3 вариант - бинарный поиск, наиболее важный вид многоступенчатого поиска. Задаются левая и правая границы интервала поиска: А=0 и В=М+1 (интервал охватывает весь массив). Вычисляется середина интервала i=(A+B)/2 с округлением в меньшую сторону. Ключ i-ой записи p(i) сравнивается с q. Если p(i)=q, поиск заканчивается. Если p(i)>q, записи с номерами от i до M включительно заведомо не содержит ключа q. Интервал сокращают вдвое, приняв B=i. Аналогично, при p(i)<q принимают A=i. Далее середина интервала вычисляется заново и действия повторяются. Если будет достигнут интервал [A, B] нулевой длины, то требуемой записи в массиве нет.

Максимальное число сравнений при бинарном поиске C_m=log₂M. Среднее число сравнений составляет C=log₂M-1.

Лучший метод поиска определяется из следующих рассуждений. Во всех трех случаях время поиска - функция от числа записей М:

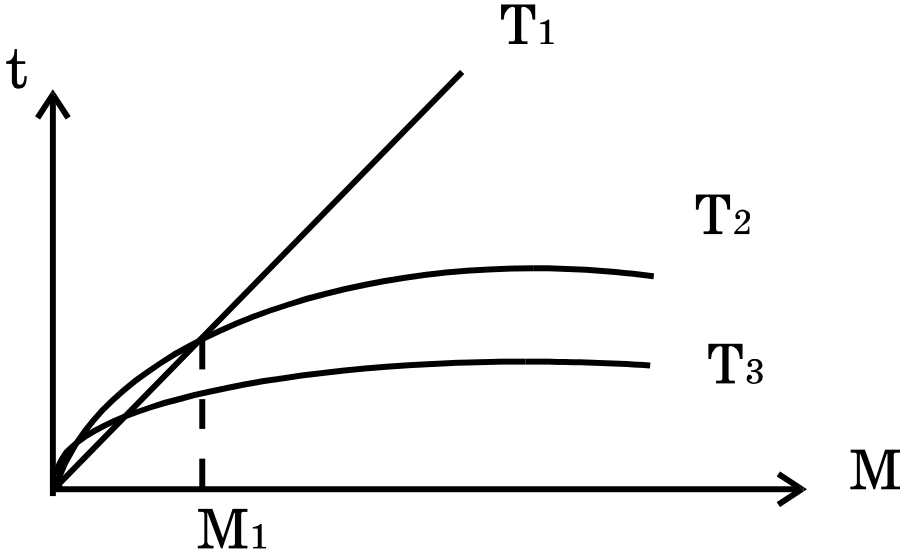
Т₁  М или Т₁=K1M

T₂  M или Т₂=К2М

Т₃  log₂M или Т₃=К3log₂M

Коэффициенты пропорциональности K1, К2 и К3 определяются быстродействием компьютера, языком и стилем программи-рования. Они влияют на граничную величину М1, выше которой преимущество бинарного поиска безусловно.

Корректировка массива может касаться одной записи или группы записей. Отдельная запись может включаться в массив и исключаться из него. Кроме того, в записи могут быть изменены значения отдельных атрибутов (как правило, неключевых). В любом случае перед непосредственной корректировкой выполняется поиск корректируемой записи. Включение новой записи в упорядоченный последовательный массив не должно нарушать его упорядоченность. Выполняемые при этом действия: поиск места вставки, сдвиг элементов массива вправо от места вставки, непосредственно вставка.

Следовательно, время корректировки составляет Тк  log₂M+ML (при бинарном поиске). L - длина одной записи. На практике ML >> log₂M, поэтому Tk  ML.

Аналогичная оценка используется для исключения записи.

Из этих оценок можно сделать вывод, что включение и исключение записей поодиночке - длительные процедуры. Поэтому в ряде случаев целесообразно накапливать корректирующие записи в специальном массиве изменений, а не вносить их поодиночке. Этот массив имеет размер в несколько процентов от основного, он упорядочен. При необходимости обработки основного массива он объединяется с массивом изменений. Слияние массивов выполняется по следующему алгоритму:

- ключ очередной записи основного массива сравнивается с ключом очередной записи массива изменений, и запись с меньшим значением ключа добавляется в новый массив (результат слияния);

- когда все записи одного из массивов будут перезаписаны полностью, оставшиеся записи другого массива добавляются в результирующий массив, на этом алгоритм заканчивается.

Если требуется использовать методы организации данных, которые позволили бы связать физически разнесенные в памяти данные в логическую последовательность, определяющую порядок их обработки, применяют списковую (цепную) организацию данных.

Список - множество записей, занимающих произвольные участки памяти, последовательность которых задается с помощью адресов связи. Адрес связи - атрибут, в котором хранится номер записи, обрабатываемой после данной записи. Обычная последовательность обработки записей в списке определяется возрастанием значений ключа в них.

В списке выделяется собственно информация (записи с содержательными сведениями) и ассоциативная информация, т.е. адреса связи.

Описание записей списка может быть произведено двумя способами (иллюстрируем их средствами языка программирования Паскаль):

1. определение адресов связи как начальных адресов записей

type link = ^zapis;

zapis = record

key: integer; {ключ записи}

other: string [30];{остальные атрибуты}

next: link

end

2. определение адресов связи как номеров записей

const M=20;

type zapis = record

key, next: integer;

other: string [30]

end;

Второй вариант более практичен, особенно если информация хранится во внешней памяти.

Возможны 2 способа организации списков:

- совместное размещение собственной и ассоциативной информации, запись и адрес связи образуют единое целое;

- раздельное размещение, где используется списковая организация адресов связи и последовательное хранение собственной информации.

При формировании упорядоченного списка записей возможно:

- вновь поступающие записи вставлять так, чтобы не нарушать упорядоченность по ключу, или

- создать сначала неупорядоченный список, а затем отсортировать его.

Второй вариант более целесообразен (использует метод слияния). В итоге время формирования упорядоченного списка оценивается, как

T  Mlog₂M.

Для поиска данных в однонаправленном списке целесообразен единственный метод - последовательный поиск, здесь Т  М. Бинарный поиск может быть реализован только последовательно и время его можно оценить, как

T  M/2+M/4+M/8+... или T  M.

Следовательно, здесь бинарный поиск неэффективен.

Для ускорения доступа к списку используют двунаправленные и кольцевые структуры.

Списковые структуры используют цепной каталог - сплошной участок памяти (или несколько таких участков), в котором одновременно размещается список обрабатываемых записей и список свободных позиций памяти. Адреса связи в цепном каталоге могут быть представлены номерами записей.

Пример описания цепного каталога на языке Паскаль

Const M=9

type

zapis = record

key, next: integer

end;

var

t:array [1..M] of zapis

В этом описании key - ключ, next - адрес связи.

Включение и исключение записей в цепном каталоге предполагает поиск местоположения включаемой (исключаемой) записи и замену значений адресов связи для установления новой последовательности записей основного списка и списка свободной памяти.

Оценка времени корректировки складывается из времени поиска и времени на замену значений адресов связи. Число пересылок адресов связи всегда одинаково и не зависит от числа записей в цепном каталоге, поэтому доминирующими являются затраты времени на поиск, и время корректировки оценивается, как Т  М.

Древовидная организация данных (дерево) - множество записей, расположенных по уровням так, что на 1-м уровне имеется только одна запись (корень дерева), а к любой записи, i-го уровня ведет адрес связи только от одной записи (i-1)-го уровня. Количество уровней в дереве называется рангом. Записи дерева, которые адресуются от одной записи (i-1)-го уровня, образуют группу. Максимальное число записей в группе называется порядком дерева.

Наиболее распространены деревья порядка 2 (бинарные), основным элементом которых является структура: вершина (ключ), левая ветвь, правая ветвь. Они интересны тем, что составляющие их записи могут быть упорядочены. Для этого один из атрибутов записи объявляется ключевым. Записи, у которых заполнены 2 адреса связи, называются полными, записи с одним адресом связи - неполными, записи с двумя незаполненными адресами - концевыми.

В упорядоченном бинарном дереве значение ключевого атрибута каждой записи должно быть больше, чем значение ключа у любой записи на левой ветви, и не меньше, чем ключ любой записи на ее правой ветви. Это определение позволяет также различать левые и правые адреса (ветви).

Упорядоченное бинарное дерево формируется из неупорядоченного массива по специальному алгоритму. Он создает корень дерева из первой записи массива с ключом p1. Значение ключа второй записи p2 сравнивается с p1, находящимся в корне дерева. Если p2<p1, то вторая запись помещается на левой от корня ветви, в противном случае - на правой. По этому же правилу на каждом следующем шаге создается очередная ветвь. Действия повторяются до исчерпания элементов массива.

Аналогично производится поиск по заданному ключу. Здесь либо достигается нужная вершина, либо поиск заканчивается, когда у какой-либо записи отсутствует адрес связи для продолжения поиска.

Оценка числа операций по формированию упорядоченного бинарного дерева C  Mlog₂M. Оценка числа сравнений при поиске записи C  Mlog₂M.

Оценки показывают преимущество бинарного дерева - минимальное время поиска (самый важный критерий).

5.2. Методы ускорения доступа к данным

Ускорение доступа к данным достигается применением принципиально новых методов размещения информации в памяти, либо созданием массивов вспомогательной информации о хранимых данных.

Доступ к требующимся записям может осуществляться не только путем сравнения искомого значения ключа с ключами записей массива по определенному алгоритму, но и в результате вычисления местоположения записи.

1) Интерполяционный поиск.

Записи исходного массива упорядочены некоторым алгоритмом сортировки. Значения ключевого атрибута p(i) для 1<i<M интерполируются с помощью линейной функции, которая строится по точкам (1, p(1)) и (М, р(М)). Для произвольной точки (i, M(i))

Если ведется поиск по значению ключевого атрибута q, подставим в формулу q вместо p(i), тогда получим номер искомой записи i по формуле:

Поскольку реальное расположение записей в отсортированном массиве соответствует линейной функции приближенно, интерполяционный поиск необходимо завершить последовательным поиском значения q, начиная с i-й записи.

2) Для упорядочения поиска может быть использована специальная расстановка записей в памяти, которая, вообще говоря, нарушает типичную при последовательной организации упорядоченность записей по значениям ключа.

Расстановка записей происходит в соответствии с так называемой адресной функцией (ХЭШ-функция или рандомизирующая функция).

Адресная функция имеет вид i=f(p), где i - номер записи, р - значение ключевого атрибута в записи. Записи, имеющие одинаковые значения i, называются синонимами. Основные требования к адресной функции:

- она должна быть аналитически задана и быстро вычисляться;

- ключевые атрибуты, подчиняющиеся произвольному распределению, функция должна переработать в равномерно распределенные (обычно это условие выполняется приближенно);

- число записей-синонимов должно составлять 10-20% от общего числа записей.

Простейшая адресная функция i=p-a, где a=const. Обозначим минимальное значение ключевого атрибута в массиве - р1, максимальное - р2. Тогда a=p1-1. Необходимый участок памяти для данных оценивается b=p2-p1+1 запись. Записи-синонимы связываются в цепочки с помощью адресов связи, они занимают дополнительную (резервную) память.

Пример: массив 13, 11, 14, 15, 11, 17, 14.

р1=11, р2=17, b=17-11+1=7.

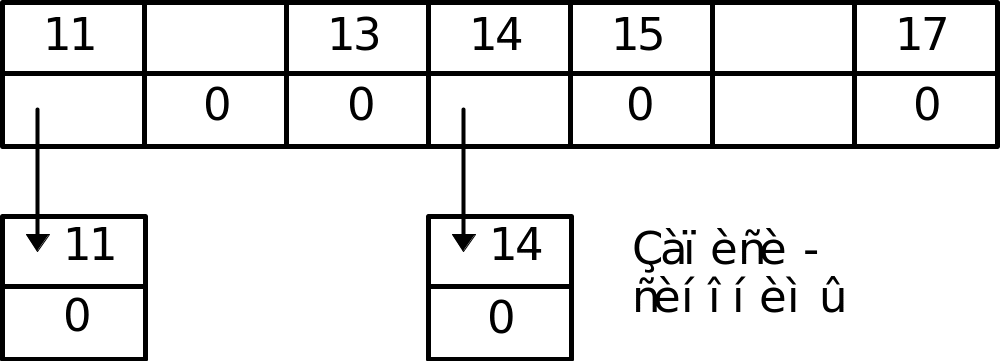
При доступе к записи q вычисляется i=f(q) и производится обращение к i-й записи. При необходимости извлекаются записи-синонимы.

Недостаток адресной функции i=p-a - большой объем неиспользуемой памяти, если р”-p>>M.

Указанного недостатка лишена функция вида i=ОСТ(p/m) - остаток от деления р на целое число m. Эта операция представляется в языках программирования, как деление числа р по модулю m, где m - простое число, непосредственно больше или непосредственно меньше числа записей М.

Для хранения информации выделяются две зоны памяти - основная и резервная. Основная зона содержит m записей, резервная предназначена для размещения записей-синонимов. При формировании данных согласно адресной функции сначала заполняется основная зона. Если позиция основной зоны, полученная при вычислении, уже занята, то текущая запись помещается в резервную зону и адресуется из этой позиции основной зоны. В дальнейшем при такой ситуации наращивается цепочка записей в резервной зоне.

3. Массив индексов

Индексом называется набор ключей и адресов записей, которые выбираются из основного массива по определенному закону. Отдельный элемент набора индексов также называется индексом.

Имеется 3 практически важных разновидности индексов:

а) информация о каждой записи основного массива попадает в индекс; это так называемая сплошная индексация;

б) номера записей, информация о которых выносится в индекс, образуют арифметическую прогрессию с шагом d>1; основной массив, дополненный таким индексом, называется индексно-последователь­ным;

в) ключи записей, информация о которых выносится в индекс, приближенно образуют арифметическую прогрессию.

Сплошной индекс связан с созданием инвертированного массива ключевых атрибутов к основному массиву.

Основной массив Инвертированные массивы

Адреса	Ключевые атрибуты			ключ А		ключ В
записей	А	В		a1		b1
400	a1	b1		400		400
500	a2	b1		900		500
600	a2	b2		a2		700
700	a3	b1		500		b2
800	a2	b3		600		600
900	a1	b3		800		b3
				a3		800
				700		900

Элементы, составляющие инвертированный массив, называются группами. Каждая группа содержит значение ключевого атрибута, имеющееся в массиве, и набор адресов записей, содержащих этот ключ. Сами группы являются записями неопределенной длины.

В информационно-поисковых системах ключевые атрибуты соответствуют ключевым словам, определяющим тематику документа. Количество ключевых слов для документа может быть любым.

Основной массив			Инвертированный массив
100	BE		A	B	C	D	E
150	ACE		150	100	150	200	100
200	DBA		200	200	250		150
250	EC						250

Связь основного и инвертированного массива в этом случае выглядит иначе.

Эффект инвертированного массива проявляется при поиске данных по нескольким условиям. Например, требуется найти все записи, содержащие ключевые слова А и С. Система обращается к инвертированному массиву, находит группы ключей А и С. Совпадающие значения адресов дают в примере запись с адресом 150.

Логические связки в запросах могут быть любыми. Например, при обработке запроса “Найти все записи, содержащие ключи С или Е, кроме А” (в терминах теории множеств СЕ\А) производится последовательное вычисление логического выражения ({150,250}{100,150,250})\{150,200}={100,250}.

Таким образом, запросу удовлетворяют записи с адресами 100 и 250.

Отметим, что поиск по инвертированному массиву обнаруживает только адреса записей и плохо приспособлен для указания всех ключей, связанных с найденной записью. Между тем, эта информация часто запрашивается.

4) Индексно-последовательный массив

Это последовательный массив, отсортированный по значениям ключевого атрибута, к которому создается дополнительный массив индексов. В индекс выносится информация о записях, номера которых образуют арифметическую прогрессию с шагом d (ниже в схеме принят шаг d=3).

П оиск значения q производится в 2 этапа:

1 этап - в массиве индексов (который отсортирован в силу упорядоченности основного массива);

2 этап - среди записей основного массива, которые расположены между двумя соседними индексами, найденными на 1-й стадии.

Применение индексов приводит к ускоренному доступу, если основной массив расположен на устройстве внешней памяти, а массив индекса - полностью в оперативной.

5. Рандомизация индекса (адресная функция для индекса).

Здесь ключи записей, информация о которых выносится в индекс, образуют приближенно арифметическую прогрессию. Индекс с номером n хранит адрес записи основного массива, ключ которого равен или непосредственно больше значения

p(1)+z(n-1),

где z - константа (шаг арифметической прогрессии), р(1) - значение ключа 1-й записи основного массива.

Примечательно, что значения ключей здесь хранить не нужно.

Поиск в рандомизированном индексе осуществляется так:

1. Номер требуемого индекса определяется по формуле

Результат деления округляется в меньшую сторону.

2. Интервал записей основного массива определяется адресами, указанными между n и n+1 индексами.

Частным случаем доступа к данным является обработка информации по нескольким ключевым атрибутам. В структуре массива определяется несколько ключевых атрибутов, причем в различных прикладных программах доступ к записям требуется осуществлять по различным сочетаниям этих атрибутов. Возможна последовательная обработка всего массива. В таких случаях устанавливается порядок старшинства атрибутов.

В СУБД таким образом может быть установлено индексирование.

Для доступа к данным по нескольким ключевым атрибутам используется мультисписковая организация данных. Мультсписок - это множество списков, организованных на общем множестве записей. Если требуется доступ к записям по К ключам, то формируется К списков для каждого ключевого атрибута в отдельности.

Пример мультисписка:

Фамилия	Профессия
	слесарь	токарь	электрик
Белов Бунин Иванов Ильин Петров Попов	А(3) А(6) А(8) А(11)	А(1) А(4) А(9) А(12)	А(2) А(5) А(7) А(10)

Здесь ключевые атрибуты - фамилия и профессия. А(i) - номера записей, которые содержат именно эти значения в качестве ключей.

В простейшем случае мультисписок состоит из двух списков:

- указатель ФАМИЛИЯ - (А(1), А(2), А(3),..., А(11), А(12),

- указатель ПРОФЕССИЯ - (А(3), А(6), А(8), А(11), А(1),..., А(12), А(2), ..., А(10)).

При размещении мультисписка во внешней памяти необходимо размещать каждый список в небольшом числе расположенных последовательно участков, что позволит уменьшить время доступа. Эффективная организация мультисписка предполагает следующее:

- число записей в каждом списке должно быть небольшим,

- адреса хранения записей должны монотонно возрастать.

Для сокращения длины списков можно детализировать содержимое указателей. Например:

1) Фамилия = “Б”  (А(1), А(2), А(3), А(4))

2) Фамилия = “И”  (А(5), А(6), А(7))

3) Фамилия = “П”  (А(8), А(9),..., А(12))

4) Профессия = “Слесарь”  (А(3), А(6), А(8), А(11)) и т.д.

При поиске в сокращенных списках необходимо сначала проанализировать все указатели, чтобы выбрать список, заведомо содержащий требуемую информацию.

Пример: пусть сформирован запрос на отбор данных по критерию

Фамилия = “Иванов” И Профессия = “Слесарь”

Для реализации запроса требуется 3 обращения к памяти для выбора списка (А(5), А(6), А(7)) и 3 обращения для выбора списка (А(3), А(6), А(8), А(11)). По сравнению списков находится запись А(6).

5.3. Организация данных во внешней памяти компьютера

Основные устройства внешней памяти компьютера - магнитные диски и магнитные ленты. В отличие от оперативной памяти здесь время доступа к данным зависит от места расположения данных на диске или ленте (требуется время на подвод нужного участка к механизму чтения-записи).

Данные во внешней памяти хранятся в виде файлов. Файл - множество логически связанных записей. В простейшем случае файл - последовательный массив записей.

Серьезным фактором, влияющим на время доступа к данным, является взаимное расположение файлов и записей на магнитном носителе. Его характеризуют адресным расстоянием - разностью адресов предыду­щего и текущего обращений к памяти dA=|A(i-1)-A(i)|.

Рассмотрим магнитный диск. С диска читается (записывает­ся) не один символ (байт), а сектор или блок данных размером обычно 512 байт. Время доступа к гибкому диску (FDD) - 200-500 мс, к жесткому (HDD) - до 10-12 мс.

Размер сектора оговорен конструкцией диска и не зависит от проектировщика системы. Обмен дисковой памяти с оперативной происходит только целыми секторами. Поэтому оптимальные длины записей, при которых достигается минимальное время обмена, должны быть кратными длине сектора. Правда, выигрыш по сравнению с записями, пересекающими границу сектора, составляет всего 2-5%.

Операционная система отводит часть оперативной памяти под буферы ввода-вывода. Каждый буфер имеет размер сектора, а их количество задается пользователем. При попытке чтения какого-либо сектора из внешней памяти операционная система ищет его сначала среди буферов, и только в случае его отсутствия происходит реальное чтение из внешней памяти. Считанный сектор занимает свободный буфер или вытесняет из одного из буферов давно не используемую информацию.

Во внешней памяти несколько смежных секторов (обычно 2 или 4, а вообще - до 16) образуют кластер. При создании файла ему отводится один кластер. Если информация выходит за пределы кластера, файлу отводится новый кластер из числа свободных на диске. Он может быть несмежным с первым и связывается с ним в цепочку. Длина цепочки ограничивается только наличием свободных кластеров.

На диске выделяется место под таблицу размещения файлов (FAT - File Allocation Table), остальное пространство диска используется для размещения файлов. В таблице хранятся описания файлов и соответствующие им списки (цепочки) кластеров.

Доступ к файлу начинается с обращения к FAT и поиска имени файла, при успешном поиске становятся доступны кластеры файла в области размещения файлов. При записи на диск нового файла в FAT предоставляется очередная свободная строка, а в области размещения файлов - очередные свободные кластеры.

При удалении файла первый символ имени файла в FAT заменяется служебным символом (обычно знаком вопроса). В результате имя файла и занимаемые им кластеры становятся недоступными, однако содержимое кластера не уничтожается, пока на диск не записываются новые данные (в последнем случае возможна потеря содержимого этих кластеров). Это дает возможность восстановить файл (например, утилитой UNERASE из пакета Norton Utilites). Новый файл может занимать кластеры в разных местах диска (не сплошной участок) - фрагментация (сегментация) файла, что может привести к существенному замедлению работы с диском. Этот эффект можно устранить, выполнив дефрагментацию файлов на диске, например, утилитой SPEEDISK из того же пакета утилит.

Существует ряд стандартных методов организации файлов на магнитном диске и соответствующих методов доступа к ним.

1. Последовательный файл

Доступ к элементам файла возможен только в направлении от начала к концу файла. Переход в обратном направлении невозможен, единственный путь - закрыть файл, открыть его снова и двигаться от начала к нужной записи.

2. Индексно-последовательный файл

Это последовательный файл, снабженный индексами. На диске для него выделяется 3 области:

а) первичная - в ней располагаются упорядоченные по значениям ключа записи, когда файл создается;

б) индексная; в зависимости от размера первичной области могут создаваться один, два или три уровня индексов. Индекс 1 уровня отмечает последовательную запись каждой дорожки диска. Индекс 2 уровня - последнюю запись каждого цилиндра диска. 3 уровень используется, если файл индекса 2 уровня достаточно велик.

в) область переполнения - для размещения записей, включаемых в файл.

Характеристики индексно-последовательного доступа:

- значения ключей должны быть отсортированы,

- в индекс заносится наибольший ключ для всех записей блока (дорожки);

- наличие повторяющихся ключей недопустимо;

- эффективность доступа зависит от числа уровней индексации, распределения памяти для размещения индекса, числа записей в файле и размера области переполнения.

3. Индексно-произвольный файл

В индекс помещается информация о ключе каждой записи. Записи файла при этом могут быть не упорядочены. Индекс формируется практически всегда как многоуровневый. Типичная организация соответствует понятию В-дерева. Нижний уровень образуют индексы со ссылкой на каждую запись основного массива, они разделены на страницы, и в конце каждой страницы оставляется резервная память. Последний индекс каждой страницы поступает на страницу предыдущего уровня В-дерева и т.д. Минимальное время доступа образует В-дерево с числом уровней, примерно равным lnM.

Корень В-дерева обычно имеет 2 ветви. Количество ветвей на следующих уровнях, в принципе, не ограничено. Ниже приведен пример схемы такого В-дерева.

Достоинство В-дерева - его простое расширение. При переполнении у какой-либо страницы половины ее содержимого индекс переходит в новую страницу, а на вышестоящем уровне появляется новый индекс.

4. Файл прямого доступа

Соответствует файлу, использующему адресную функцию вида i=p-a.

Особенности прямого доступа:

- не требуется упорядоченность записей файла,

- наличие повторяющихся значений ключа недопустимо,

- значениям нескольких ключей может соответствовать один и тот же адрес.

Отметим, что прямой метод доступа обеспечивается многими языками программирования.

Доля выборки записей	Наилучшая организация файла
единицы записей 0...10% 10...100%	Прямого доступа Прямой, индексный последовательный

На выбор между перечисленными методами существенное влияние оказывает количество записей, которые должны быть обработаны в процессе реализации запроса. Этот параметр называется долей выборки и равен отношению числа требуемых при выборке записей файла к общему числу записей в файле. Рекомендации к выбору метода организации файла дает следующая таблица: