4.4. Приложение к лабораторной работе № 2

4.4.1.Уточнённая модель (B₀ B₁).

Учтём отличие вращательных констант молекулы B₀ B₁ в её основном и первом возбуждённом колебательных состояниях.

Используя уравнения (3.22) и (3.23), а также правила отбора, для волновые числа переходов в Р-ветви (J = 1) можно представить следующим образом:

= ₀ + В₁ (J-1) J – B₀ J(J+1) (4.1)

Для R-ветви J = +1 и частота перехода получится:

₀ + B₁ (J + 1)(J+2) - B₀ J(J+1) (4.2)

1) Расстояние между двумя линиями с одинаковыми значениями J нижнего уровня P- и R- ветвей составит

= B₁ (J + 1)(J+2)  В₁ J(J-1) = 2B₁ (J +1). (3.24)

Отсюда легко найти B₁.

2) Сравнивая переходы со сдвигом квантовых чисел J_R = J_P 2, можно рассчитать B₀:

=[B₁J(J1) В₀ (J 1)(J2)]  [B₁ (J 1) J  В₀ J(J+1)]= = B₀ ( 4J  2)= 2B₀ ( 2J  1) _. (3.25)

4.4.2. Дистанция между ближайшими линиями разных ветвей равна

_R(0)  _P(1) = [ ₀ + 2B₁] – [ ₀  2B₀] = 2 (B₁ + B₀)  4 B_{среднее}. (4.3)

Диаграмма переходов в колебательно-вращательном спектре двухатомных газов представлена на рис. 3.3.

4.4.3. Пример. Обработка колебательно-вращательного ик-спектра газа hf

Таблица 3.5.4.

	P-ветвь	R-ветвь	Сдвиги частот (волновых чисел), см-1
J
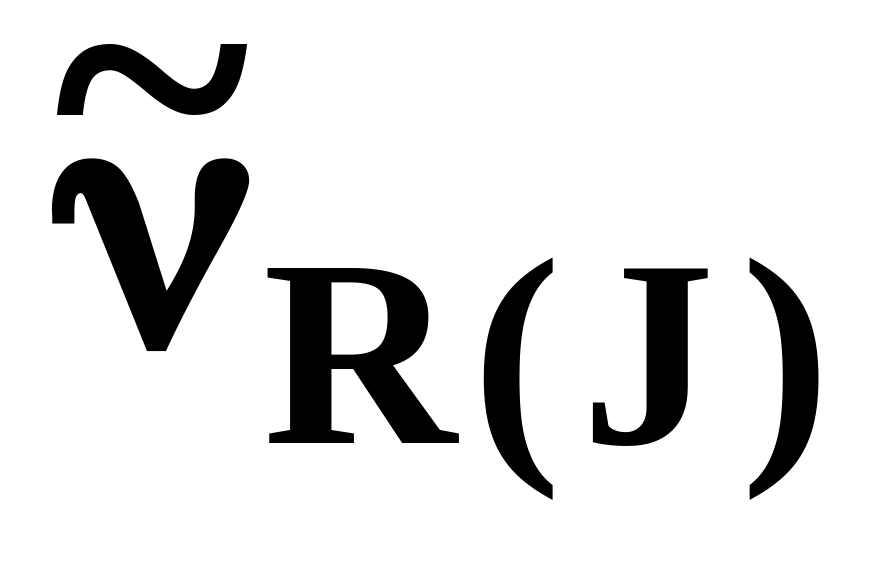
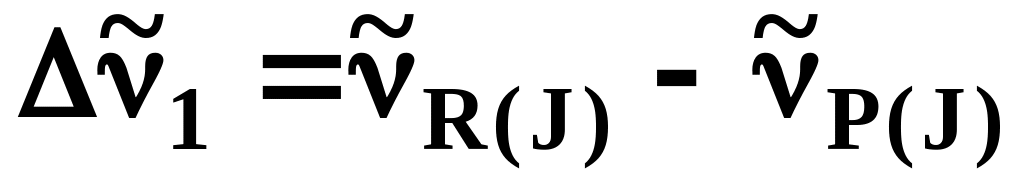
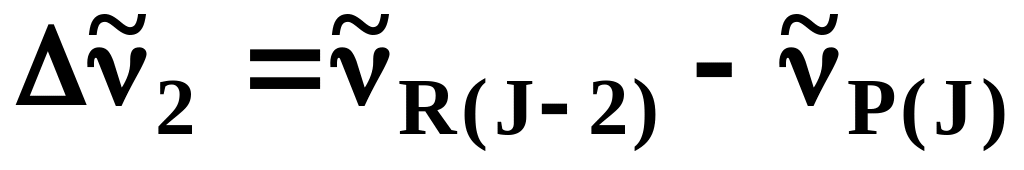
0	-	3998	-	-
1	3917	4035	118	-
2	3874	4071	197	124
3	3830	4105	275	205
4	3785	4137	352	286
5	3738	4166	428	367
6	3689	4193	504	448
7	3637	4214	577	529
8	3590	4238	649	604

По данным таблицы построены графики зависимостей (рис.4.1) :

f(J) и f(J) .

Рис. 4.1. Сдвиги частот в колебательно-вращательном спектре газообразного HF (к расчету вращательных постоянных В₀ и В₁)

Далее рассчитаны структурные характеристики молекулы:

А) Вращательная постоянная основного колебательного уровня

В₀ = /4 = 20,5 см^-1;

51

Б) Момент инерции:

I₀ = ,

В) Приведённая масса = ,

Г) Межатомное расстояние r_HF = = ,

Д) Вращательные уровни энергии в приближении жёсткого ротатора

E_J= hcB₀J(J+1)=6,62.10^-34Дж.с3.10⁸м/с.20,5.10²м^-1J(J+1)

E_J=4,0710^-22J(J+1) Дж,

J =0,1,2,3,...; E_J10²² = 0; 8.14; 24.42; 48.84; ... Дж

Е) Статистические веса вращательных (ротационных) уровней

g_J=2J +1; J =0,1,2,3,...; g_J=1,3,5,7,...

Ж) Факторы Больцмана вращательных уровней f_J = exp(-EJ/kT) (см. табл.)

З) Ненормированные заселённости вращательных уровней (ненормирован-ные вероятности)

g_Jf_J = g_J  exp(-E_J/kT)= (2J +1)  exp(-E_J/kT) (см. таблицу).

И) Вращательная сумма состояний (по приближённой формуле)