Числовые и функциональные ряды
301.-310. Исследовать на сходимость ряд.
301. 
302. 
303. 
304. 
305. 
306. 
307. 
308. 
309. 
310. 
311.-320. Исследовать на абсолютную и условную сходимость ряды.
311. 
. 312. 
313. 
314. 
315. 
316. 
317. 
318. 
319. 
320. 
321.-330. Разложить функцию f(x) в ряд по степеням x .
321. 
322. 
323. 
324. 
325. 
326. 
327. 
328. 
329. 
330. 
331.-340. Разложить в ряд Фурье в указанном интервале функцию f(x). Построить график этой функции и график суммы полученного ряда Фурье.
331. 
в
интервале (-1, 1).
332. 
в
интервале (0, 3) по синусам.
333. 
в
интервале (-,
).
334. 
в
интервале (-,
).
-/2, x(-, 0),
335. 
0, x
= 0, в интервале (-,
).
/4, x (0, )
336. 
в
интервале (-2, 2).
337. 
в
интервале (0, 2)
по косинусам.
338. /4 – x/2 в интервале (0, ) по синусам.
339. 
в
интервале (-,
).
340. ( – x)/2 в интервале (0, ) по синусам.
Кратные и криволинейные интегралы
341.-350. Вычислив с помощью замены переменных двойной интеграл, найти площадь фигуры, ограниченной заданными линиями.
351.-360. С помощью двойного интеграла найти объем тела, ограниченного поверхностями, уравнения которых заданы.
361.-370. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями.
371.-380. Вычислить криволинейный интеграл второго рода вдоль заданной линии. Для незамкнутых кривых ориентация соответствует возрастанию параметра t или переменной x. Для замкнутых кривых направление обхода предполагается положительным.
L– отрезок прямой,
от точки (0;0) до (
;2).
L – дуга линии
от точки (0;0) до точки (1;1).
L
– дуга линии
от точки (0;0) до точки (1;1).
L–
дуга окружности
L
– эллипс
L–
дуга окружности
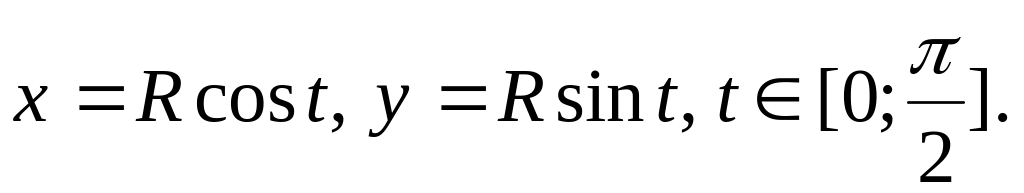
L
– линия
,
x[-1;1].
L
– линия y = 1- |1-x|,
x[0;2].
L– арка циклоиды
L
– окружность x2
+ y2 = R2.
381.-390. Дано скалярное поле
и векторное поле
.
Найти
,
и
в точке
.
.
.
.
.
.
.
391.-400. Найти поток векторного поля
через часть плоскости
,
расположенную в первом октанте (нормаль
образует острый угол с осью
).
401.-410. Доказать потенциальность поля
и найти его потенциал
.
Специальные разделы
411.-420. Восстановить аналитическую функцию f(z) = u+iv по заданной действительной или мнимой части.
411. 
. 412. 
. 413. 
.
414. 
. 415. 
. 416. 
.
417. 
. 418. 
. 419. 
.
420. 
.
421.-430. Найти все особые точки функции
и определить их характер. Разложить
в ряд Лорана в указанном кольце.
421. 
.
422. 
.
423. 
.
424. 
425. 
426. 
427. 
428. 
.
429. 
430. 
.
431.-440. Средствами операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
431. x + 2x –3x = e - t, x(0) = 0, x(0) = 1.
432. x + 2x = t sin t, x(0) = 0, x(0) = 0.
433. x + 2x + x = sin t, x(0) = 0, x(0) = –1.
434. x + 2x + x = t2, x(0) = 1, x(0) = 0.
435. x + 2x + 2x =1, x(0) = 0, x(0) = 0.
436. x + x = cos t, x(0) = 2, x(0) = 0.
437. x – 2x +5x = 1–t, x(0) = 0, x(0) = 0.
438. x + 2x + x = t, x(0) = 0, x(0) = 0.
439. x – 2x + x = t – sin t, x(0) = 0, x(0) = 0.
440. x + x = t cos2t , x(0) = 0, x(0) = 0.
441.-450. Используя теорию вычетов, вычислить интегралы.
441. 
. 442. 
.
443. 
. 444. 
.
445. 
. 446. 
447. 
448. 
.
449. 
450. 
451.-460. Однородный упругий стержень длины l изготовлен из материала с плотностью и модулем упругости E. Стержень имеет постоянное поперечное сечение площади A. Найти методом Фурье решение уравнения продольных колебаний стержня
при заданных начальных и граничных условиях.
451. u(x,0) = Px/EA, u(x,0)/t = 0;
u(0,t) = 0, u(l,t)/x = 0.
452. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = 0, u(l,t)/x = P/EA.
453. u(x,0) = 0, u(x,0)/t = 0;
u(0,t)/x = P/EA, u(l,t)/x = P/EA.
454. u(x,0) = –P(l–x)/EA, u(x,0)/t = 0;
u(0,t)/x = 0, u(l,t) = 0.
455. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = P/EA, u(l,t) = 0.
456. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = 0, u(l,t) = Vt.
457. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = –Vt, u(l,t) = 0.
458. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = 0, u(l,t) = U∙sin(t).
459. u(x,0) = 0, u(x,0)/t = 0;
u(0,t) = 0, u(l,t)/x = (P/EA)∙sin(t).
460. u(x,0) = 0, u(x,0)/t = 0;
u(0,t)/x = (P/EA)∙sin(t), u(l,t) = 0 .