Вычисление интегралов, содержащих квадратный трехчлен

и

При вычислении интегралов и используется выделение полного квадрата.

ПРИМЕР 9. Вычислить .

Для квадратного трёхчлена получим

Подставим это выражение в интеграл.

ПРИМЕР 10. Вычислить .

.

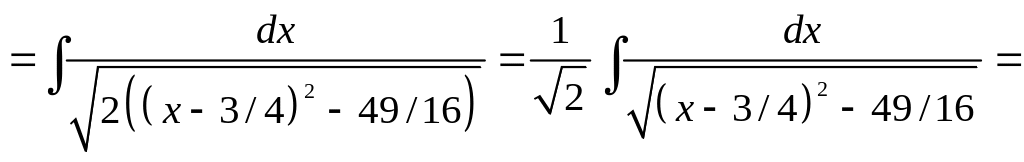
ПРИМЕР 11. Вычислить

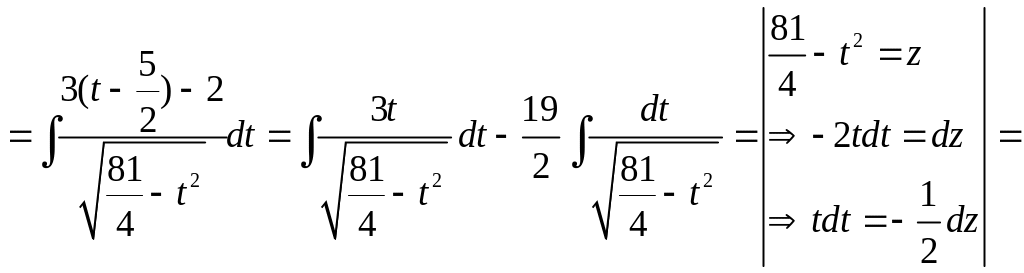
Интегрирование рациональных дробей

Интегрирование частного от деления многочлена на многочлен, так называемой рациональной дроби, происходит в несколько этапов. Прежде всего, нужно сравнить степени числителя и знаменателя. Если степень числителя меньше степени знаменателя, то дробь называется правильной. Если степень числителя больше или равна степени знаменателя, то дробь называется неправильной и из неё нужно выделить целую часть. В простых случаях для этого преобразуют числитель, в более сложных делят “уголком”. Для этого записывают оба многочлена, начиная со старшей степени, и делят старшую степень делимого на старшую степень делителя. Процедура деления проводится в той же последовательности, что и деление чисел.

ПРИМЕР 12. Выделить целую часть рациональной дроби .

_ _

__

__

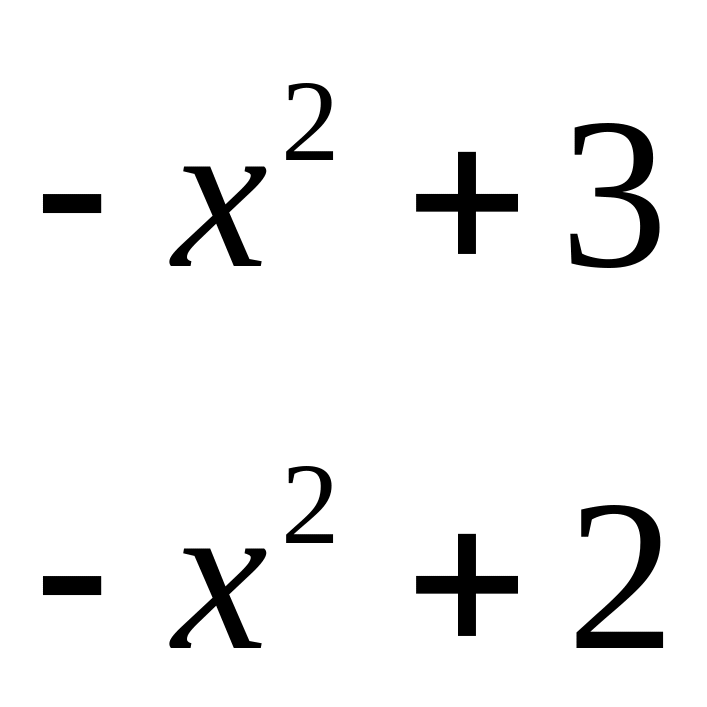
1

Итак, частное равно , а остаток равен 1. Следовательно, . То есть мы разложили неправильную дробь на сумму целой части и правильной дроби .

При затруднениях в выписывании целой части и правильной дроби, полезно рассмотреть какой-нибудь числовой пример.

Н апример, , т.к. .

2

Посмотрите внимательно, куда записано частное 1, остаток 2 и делитель 5. Здесь неправильная дробь 7/5 разложена на сумму целого числа 1 и правильной дроби 2/5.

ПРИМЕР 13. Выделить целую часть рациональной дроби .

-

-

-

-

-

45

.

Таким образом, интеграл от неправильной дроби можно разложить на сумму интегралов от многочлена и правильной дроби.

Чтобы проинтегрировать правильную дробь её нужно разложить на сумму элементарных дробей. Элементарными называют дроби следующих четырёх видов:

1. ,

2. , (n ≥ 2),

3. , где дискриминант < 0, то есть квадратный трёхчлен не имеет действительных корней;

4. , где n ≥ 2, < 0.

Чтобы представить правильную дробь в виде суммы элементарных дробей, сначала нужно разложить знаменатель на линейные и квадратичные множители:

, где квадратные трёхчлены не имеют действительных корней.

Затем правильную дробь раскладывают на сумму элементарных дробей с неопределёнными коэффициентами.

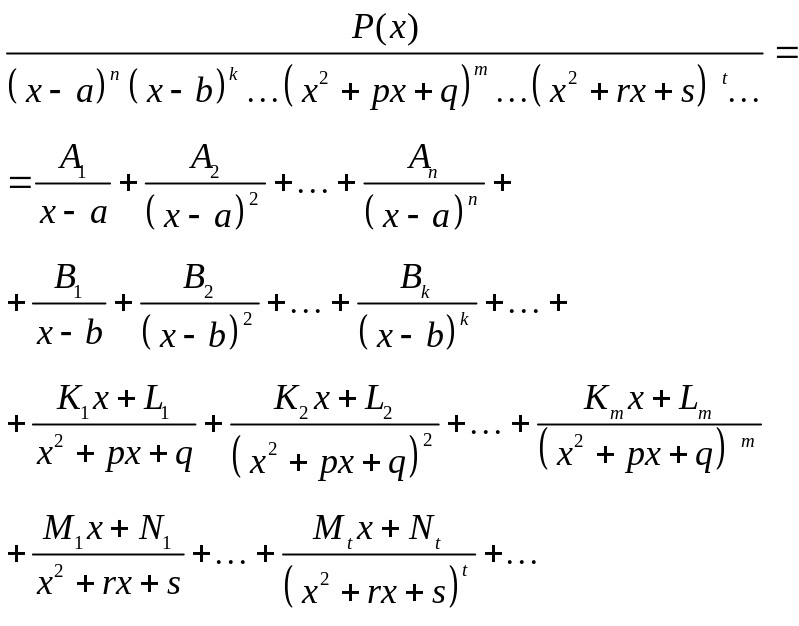
Здесь каждому сомножителю соответствует n дробей, в числителях которых стоят неизвестные пока числа , а степени знаменателей меняются от 1 до n.

Каждому сомножителю в знаменателе раскладываемой дроби соответствуют m элементарных дробей с числителями , а степени знаменателей меняются от 1 до m.

Чтобы найти неопределённые коэффициенты приводят элементарные дроби к наименьшему общему знаменателю и приравнивают полученный числитель к числителю первоначальной дроби.

ПРИМЕР 14. Разложить на элементарные дроби .

Так как знаменатели первой и последней дробей равны, то должны быть равны и числители. То есть

.

Приравняем коэффициенты при одинаковых степенях x и решим полученную систему уравнений.

Очевидно, A = -1, B = 2, C = 3, D = -1. Тогда

.

ПРИМЕР 15. Разложить на элементарные дроби .

Используем метод подстановки для вычисления коэффициентов. Эти многочлены должны быть равны при всех значениях . Поэтому при подстановке любого числа в левую и правую части, должны получаться верные равенства. В качестве значений удобно брать корни знаменателя и небольшие целые числа.

x = 1 | 3 = 3B

x = 0 | 4 = 2C

x = -2 | 18 = -18D

x = -1 | 11 = 2A – B + 4C – 4D.

Итак, A = 0, B = 1, C = 2, D = -1, то есть

.

Рассмотрим теперь интегрирование основных элементарных дробей.

1.

2.

3.

Дроби четвертого типа интегрируются аналогично.

ПРИМЕР 16. Вычислить интеграл

Так как дробь неправильная, то начинаем с выделения целой части.

_

_

Разложим правильную дробь на сумму элементарных дробей.

То есть Таким образом

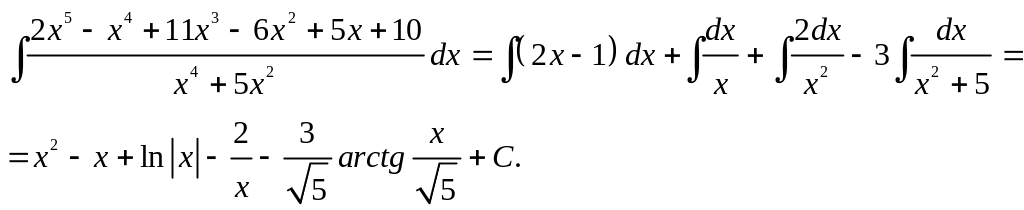
ПРИМЕР 17. Вычислить интеграл

Выделим целую часть неправильной дроби. Для этого в знаменателе придётся открыть скобки.

-

-

Разложим правильную дробь на элементарные.

Решим эту систему методом Гаусса.

~ ~

~ ~ ~

~

A = 1, B = -2, C = 0, D = 2.