2.1.5. Пространство параметров. Бифуркации. Комбинированные пространства, бифуркационные диаграммы

Б ифуркация – качественное изменение состояния системы, изменение фазового пространства (напр, измерение числа аттракторов в ФП). Мультистабильность – наличие при равных параметрах нескольких вариантов движений (аттракторов) в фазовом пространстве. Комбинированные пространства – по оси абсцисс можно отложить значение параметра, а по оси ординат – значения динамической переменной в установившемся режиме. Построенная таким образом бифуркационная диаграмма для квадратичного отображения широко используется для демонстрации универсальных закономерностей подобия при переходе к хаосу через каскад удвоений периода. Бифуркационная диаграмма – изображение смены возможных динамических режимов системы (равновесных состояний, стационарных точек, периодических орбит и пр.) при изменении значения биф. параметра.

2.2. Основания для объявления процессов случайными Использование вероятностного подхода обычно связано с признанием некоторой величины «случайной». Существует несколько точек зрения на случайность, позволяющих ввести количественные меры. Они не всегда согласуются, и на практике могут даже дать противоположные оценки.

2.2.1. Теоретико-множественный подход связывает с понятием случайности возможность задать для действительной величины з-н распределения вероятности. Непредсказуемость значения случайной величины определяется «шириной» распределения. OX – x, OY – P(x). Дисперсия характеризует размазанность распределения, и мат. ожидание – его центр.

Н ормальный з-н распределения (гауссовский шум), где a и σ² – параметры. На практике величины, которые являются результатом действия многочисленных факторов, часто распределены примерно по нормальному закону.

2.2.2. Признаки случайности, традиционные для физиков (связаны с отсечением повторимости) 1). Нерегулярная (непериодическая) форма временной. Нет периода – случайность, есть – детерминированность. 2). Спадающие корреляции. Этим признаком является убывание автокорреляционной функции ρ (τ) до 0 с ростом τ. АКФ 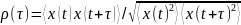. 3). Сплошной спектр. Согласно этому признаку случайным называют процесс со сплошным, непрерывным спектром; спектр периодического сигнала дискретен. 4). По виду фазового портрета (мн-в в восстановленном «фазовом пространстве»): точка, цикл, тор, странный (отсутствие признаков конечной размерности) и т.д. Существуют и другие качественные критерии: невоспроизводимость процесса и его неконтролируемость, т.е. невозможность создать условия, при которых процесс протекал бы одинаковым или заранее предписанным образом.

2.2.3. Алгоритмический подход интерпретирует «отсутствие закономерностей», как чрезмерную сложность алгоритма, требуемого для воспроизведения данного процесса в цифровом виде. Любой процесс можно представить последовательностью нулей и единиц. Колмогоров предложил считать мерой сложности такой последовательности длину минимальной программы l (в битах), которая воспроизводит последовательность {y_i}. Если единицы и нули расположены случайно, программа будет состоять в том, чтобы транслировать последовательность посимвольно: она не сжимается. l ~ N для случайных последовательностей и l << N для неслучайных.