Глава 2. Два подхода к моделированию и прогноз (вероятностный и динамический)

Динамический подход основан на вере что можно точно предсказать последующее поведение системы по знанию поведения в настоящий момент. Приверженец этого подхода – Лапласс.

Статистический – основан на признании некоторых величин «случайными» и на использовании понятия вероятности и теории вероятности.

2.1. Основные понятия и особенности динамического моделирования

2.1.1. Определение динамической системы

Динамический подход опирается на понятие динамической системы. Для того, чтобы задать динамическую систему, нужно:

1) Однозначно установить состояние системы. Состоянием (вектором состояния) называют совокупность D величин: x=(x₁, x₂,..., x_D), где D – размерность описания. Величины x_k называются динамическими переменными.

2) Задать оператор эволюции Φ_t: x(t₀+t)=Φ_t(x(t₀)), который позволяет по начальному состоянию x₀(t₀) однозначно определить состояние объекта в любой последующий момент времени.

2.1.2. Нестрогий пример. Переменные и параметры. Кошка – объект. Цель – описание эволюции ее здоровья. x1 – рост, х2 – масса, х3 – густота шерсти. D = 3. Параметры: а1 – количество еды, а2 -время прогулок. Фазовое пространство (состояний) и пространство параметров.

2 .1.3. Фазовое пространство. Консервативные и диссипативные системы. Аттракторы, мультистабильность, бассейны притяжения

С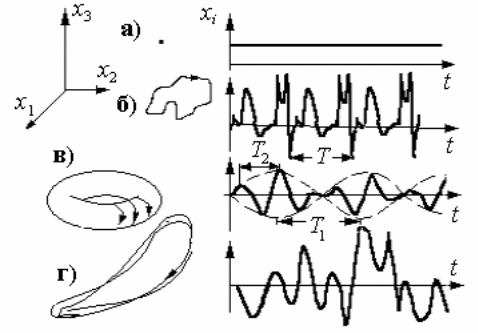 остоянию x(t) в некоторый момент t в фазовом пространстве соответствует точка с координатами x1(t), x2 (t), x3 (t) – изображающая точка. В процессе эволюции изображающая точка смещается вдоль некоторой линии – фазовой траектории. Совокупность характерных фазовых траекторий называют фазовым портретом системы. Фазовые траектории не могут пересекаться, т.к. это означало бы нарушение правила динамического описания – у одного настоящего одно будущее. В точках равновесия состояние ДС остается неизменным сколь угодно долго. В типичной фазовой траектории можно выделить начальный участок (переходный процесс) и более поздний этап движений, которые отличаются большей степенью повторяемости – установившиеся движения. Установившимся движениям в фазовом пространстве диссипативных систем соответствуют аттракторы – это состояния устойчивого равновесия. Множества точек в фазовом пространстве, из которых система попадает на аттрактор, называется бассейном притяжения данного аттрактора. Аттракторы могут существовать в пространстве состояний только диссипативных динамических систем – обладающие свойством сжатия фазового объема. В консервативных системах начальный фазовый объем сохраняется, лишь изменяя свою форму. Аттракторы существуют в пространстве состояний, бифуркации – в пространстве параметров.

Виды аттракторов в фазовом пространстве: точка соотв. состоянию равновесия; цикл – периодическому процессу (б); тор – «бесконечно тонкая нитка, наматывающаяся на бублик» – образ квазипериодических движений (с двумя характерными периодами T₁ и T₂ , находящимися в иррациональном соотношении); странный аттрактор – фрактально устроенное множество, сосредоточенное в ограниченной области фазового пространства, образ хаотических колебаний.

В фазовом пространстве систем с непрерывным временем при D = 1 могут существовать лишь состояния равновесия, при D = 2 – точки равновесия и циклы, при D ≥ 3 – все перечисленные предельные множества. Характерные черты хаотических движений: 1) неповторимость во времени; 2) сильная чувствительность к возмущению начальных условий.

Другая ситуация с аттракторами складывается в системах с дискретным временем. Вид аттрактора в их фазовом пространстве можно представить, разрезав левые картинки на рис. плоскостью (сечение Пуанкаре). Точка и однооборотный цикл дадут в разрезе одну точку. Более сложные циклы – несколько точек. Траектория на торе точками прокола секущей плоскости «нарисует» замкнутую кривую, которая в дискретной системе представляет в фазовом пространстве квазипериодическое движение. Хаотический аттрактор будет представлять собой сложно структурированный (часто, самоподобный) набор точек.

2.1.4. Характеристики аттракторов. 2.1.4.1. Геометрические характеристики. Топологическую размерность D_T: для точки устанавливается размерность D_T = 0; множество, которое может быть разделено на непересекающиеся части подмножеством размерности D_T , имеет размерность D_{T +1}. В соответствии с этими правилами гладкая линия имеет топологическую размерность D_T =1, поверхность – D_T = 2 , объем – D_T = 3. Соответственно, точка равновесия, цикл и тор имеют топологические размерности 0, 1 и 2. Странные аттракторы фрактальны (самоподобны), требуется введение фрактальных размерностей. Наиболее простая из них – емкость – оценивает только геометрию аттрактора. Вводятся и обобщенные размерности, учитывающие посещаемость его подмножеств изображающей точкой. Пример фрактала: поделим отрезок на 3, среднюю часть отбросим; повторим, и т.д. Получится группа точек, устроенная наподобие разорванного множества.

2.1.4.2. Динамические характеристики. Ляпуновские показатели характеризуют скорость разбегания или сближения изначально очень близких фазовых траекторий. Малое отклонение изображающей точки от некоторой траектории на аттракторе, т.е. малое возмущение ε₀ , до тех пор, пока оно не достигло значительных величин, эволюционирует приближенно по экспоненциальному закону вида ε (Δt) = ε₀e^λΔt. Не давая системе увеличивать возмущения ограничением отрезка времени наблюдения τ, можно вычислить показатели экспоненты: λ_i = (1/τ)ln(ε_i/ε₀). Усредненные по всему аттрактору значения этих коэффициентов называют показателями Ляпунова, Λ₁,Λ₂ ,...,Λ_D. Они характеризуют устойчивость движения на аттракторе в линейном приближении. Упорядоченный по убыванию набор значений Λ_i называют спектром Ляпуновских показателей, а последовательная запись их знаков (+, –, или 0) – сигнатурой спектра. Если (−, −, ..., −), то аттрактором является точка равновесия. Сигнатура предельного цикла – (0, −, ..., −), для двумерного тора – (0, 0, −, ..., −). В спектре ляпуновских показателей хаотического аттрактора обязательно присутствует хотя бы один положительный показатель. Странный аттрактор – (+, 0, −, ..., −), «разбегание» изначально близких траекторий. Если 2 и > положительных показателя, то говорят о гиперхаосе.