- •21. Основные теоремы динамики точки. Импульс силы. Теорема об изменении количества движения и момента количества движения
- •23. Работа силы
- •Работа силы тяжести, силы упругости и силы тяготения.
- •23. Теорема об изменении кинетической энергии
- •24. Затухающие колебания материальной точки
- •26 Механическая сиситема. Силы внутренние и внешние. Масса системы. Центр масс.
- •Масса системы.Центр масс
- •27 Момент инерции тела относительно оси. Радиус инерции. Примеры вычисления моментов инерции некоторых однородных тел.
- •Примеры вычисления моментов инерции некоторых однородных тел.
- •28. Момент инерции относительно параллельных осей. Теорема Гюйгенса.
24. Затухающие колебания материальной точки
Рассмотрим колебательное движение материальной точки под действием линейной восстанавливающей силы F и силы сопротивления движению R пропорциональной скорости в точке.
![]()
![]() ,
где
,
где
![]()
Тогда ДУ прямолинейного движения:
![]()
Обозначим через
![]() и
получим:
и
получим:
![]()
Для интегрирования (3.8) составим характеристическое уравнение и найдем его корни:
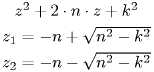
где
![]() —
частота собственных колебаний материальной
точки, а
—
частота собственных колебаний материальной
точки, а![]() характеризует
сопротивление
характеризует
сопротивление
среды.
Рассмотрим случай,
когда
![]() :
:
![]()
Тогда общее решение уравнения (3,8) имеет вид
![]()
Положим, что
![]()
Тогда из (3.9)
![]()
![]()
Движение, определяемое уравнением (3.10) имеет колебательный характер, так как х периодически меняет свой знак.
Множитель
![]() указывает
на то, что амплитуда с течением времени
уменьшается, колебание
указывает
на то, что амплитуда с течением времени
уменьшается, колебание
такого типа называется затухающим колебанием.
Величины А
и![]() определяется
следующими выражениями:
определяется
следующими выражениями:
![]()
при этом
![]()
Частота затухающих колебаний
![]()
период:
![]()
где Т— период свободного колебания материальной точки.
Из (3.11) следует,
что период затухания колебания больше
периода свободного колебания точки.
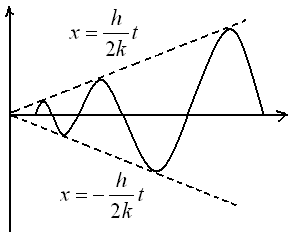
Так как
![]() ,
то есть график затухания колебаний
заключен
,
то есть график затухания колебаний
заключен
между двумя
симметричными относительно оси абсцис
кривыми:![]()

25. Вынужденные колебания. Резонанс. Вынужденные колебания при вязком сопротивлении. Амплитудно-частотная и фазо-частотная характеристики.
Колебательное движение материальной точки происходит при условии, если на точку которая отстоит от положения равновесия, действует некоторая сила F стремящаяся в эту точку, в это положение. Такая сила наз-ся восстанавливающей.
Мы будем рассм-ть случай, когда восстанавливающая сила пропорциональна отклонению от положения покоя.
![]()
Различают 2 вида вынужденных колебаний.
1)Вынужденные колебания совершаются под действием восстанавливающей
силы и силы периодического характера называемой возмущающей силой.
2)Вынужденные колебания совершающиеся под действием восстанавливающей силы, возмущающей силы и силы сопротивления дижения
Вынужденные колебания материальной точки при наличии сопротивления дижении.
Рассм-м колебание
материальной точки на которую действуют
силы восстанавливающая (
),
возмущающая сила (![]() )
изменяющаяся по гармоническому закону
и сила сопротивления (
)
изменяющаяся по гармоническому закону
и сила сопротивления (![]() )
пропорциональная скорости точки.
)
пропорциональная скорости точки.
,
,
=![]()
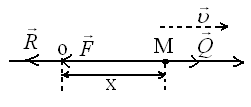
Проекция на ось х.
![]() тогда
тогда
![]()
![]()
![]() частота
возмущающей силы
частота
возмущающей силы
![]() начальная
фаза возмущающей силы, тогда
начальная
фаза возмущающей силы, тогда

(1)- это диф.ур. вынужденных колебании при наличии сопротивления движению пропорционального скорости.
Общее решение (![]() )
этого ур-я состоит слагаемых, первое из
которых яв-ся общим решением однородного
уравнения, а
)
этого ур-я состоит слагаемых, первое из
которых яв-ся общим решением однородного
уравнения, а
![]() яв-ся
частным решением (
)
неоднородного диф.ур. (1).
яв-ся
частным решением (
)
неоднородного диф.ур. (1).
![]()
![]() ещем
в виде:
ещем
в виде:
![]() допишите пожалуйста
допишите пожалуйста
В зависимости от k и n реш-е ур-я (1) будет иметь вид:
1) при k>n
![]()
2) при n>k

3) при n=k
В этом случае
![]()
Величины
![]() яв-ся постоянными интегрирования и
определяются по начальным условиям
движения.
яв-ся постоянными интегрирования и
определяются по начальным условиям
движения.
Из выражения (2)и(4) видно, что свободное колебание(первое слагаемое в решениях с течением некоторого времени, времени установления затухают и вид колебании опр-ся видом вынужденных колебании.
![]()
 м
м
![]() свободное
колебание(затухающиеся)
свободное
колебание(затухающиеся)
![]() вынужденное
колебание
вынужденное
колебание
Явление резонанса
Явление резонанса возникает при совпадении частот вынужденных, свободных колебаний точки, т.е. когда p=k.
1) Рассм. Случай когда нет сопротивлении среды, тогда

Частота и период
вынужденных колебании равна частоте k
и периоду
![]() свободных колебании точки.
свободных колебании точки.
Исследование вынужденных колебании при наличии сопротивления движению
Фаза вынужденных
колебании при наличии сопротивления
![]() отстает
от фазы взаимодействия силы
отстает
от фазы взаимодействия силы
![]() на
величину
на
величину
![]() .
.
Эту величину наз-т сдвигом фазы и поределяют
![]()
Величина
зависит
от отношения
![]() характеризующую
возмущающую силу
характеризующую
возмущающую силу
и отношение
![]() характеризующего
сопротивление среды. Построим график
характеризующего
сопротивление среды. Построим график
![]() .
.
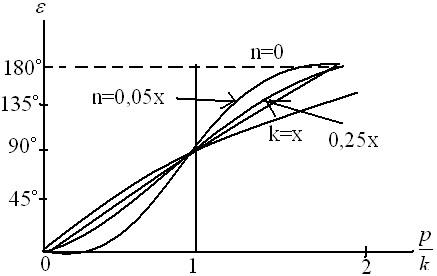
При отсутствии
сопротивления:
![]()
![]() при
при
![]() ;
;
![]() при
при
![]()
Под влиянием сопротивления этот разрыв сглаживается.
Если
![]() ,
то
,
то
![]() (коэф
затухания)
(коэф
затухания)
![]() .
Зная
.
Зная
![]() можно определить сдвиг фаз непосредственно
по этому графику. Амплитуда вынужденных
колебаний.
можно определить сдвиг фаз непосредственно
по этому графику. Амплитуда вынужденных
колебаний.
![]() Введем коэф
динамичности
Введем коэф
динамичности
![]() где
где
![]() -
это амплитуда вынужденных колебаний
при наличий сопротивления,
-
это амплитуда вынужденных колебаний
при наличий сопротивления,
![]() -
это амплитуда статического отношения
точки от начала корд, равный
-
это амплитуда статического отношения
точки от начала корд, равный
![]() ,
,![]() под действием постоянной силы.
под действием постоянной силы.
 Напишем зависимоть
Напишем зависимоть
![]()

Отсюда видно, что при отсутствии сопротивления амплитуда вынужденных колебаний стремится к бесконечности.
При наличии
сопротивления амплитуда вынужд колебании
имеет конечную величину
![]() То влияние сопротивления на вынужденные
колебания внутр точки выражается в
сдвиге фазы возмущающей силы и в
уменьшении амплитуды колебания по мере
увеличения сопротивления.
То влияние сопротивления на вынужденные
колебания внутр точки выражается в
сдвиге фазы возмущающей силы и в
уменьшении амплитуды колебания по мере
увеличения сопротивления.
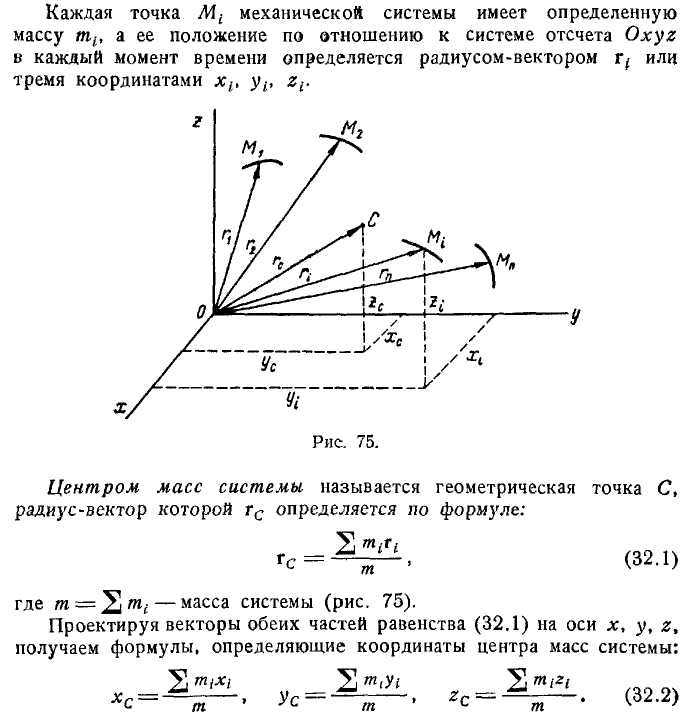
26 Механическая сиситема. Силы внутренние и внешние. Масса системы. Центр масс.





Масса системы.Центр масс