Теорема о работе равнодействующей

Т еорема: Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Допустим, что на точку действуют силы 

Равнодействующая этих сил 

Если точка M получает элементарное перемещение  , то элементарная работа равнодействующей силы  на этом перемещении

. Для вычисления работы равнодействующей силы на участке  воспользуемся формулой (3.103)

, или .

Вычисление работы в некоторых частных случаях: работа постоянной силы на прямолинейном перемещении, работа сил тяжести

Такой случай может иметь место,  когда действующая сила  постоянна по модулю и направлению (F= const), а точка, к ко­торой приложена сила, движется прямолинейно (рис.7}. В этом случае   и работа силы   .

Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).

  

1) Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу весом  , будет равна  , где   и  - координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна

,

где Р - вес системы,  - вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действую­щих на систему, вычисляется как работа их равнодействую­щей Р на перемещении центра тяжести (или центра масс) системы.

Работа силы, приложено к вращающемуся телу

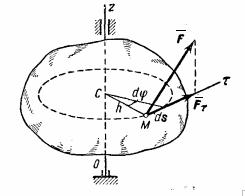
Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.27) будет равна

,

так как  , где  - угол поворота тела.

Но, как легко видеть,  . Будем называть величину   вращающим моментом. Тогда получим:  .

Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать  .

При повороте на конечный угол   работа будет равна

,а в случае постоянного момента  .

Если на тело действует пара сил, лежащая в плоскости, перпендикулярной к оси Оz, то Мz будет, очевидно, означать момент этой пары.

Укажем еще, как в данном случае определяется мощность

.

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощ­ности вращающий момент будет тем больше, чем меньше угловая скорость.

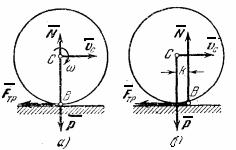
Работа силы трения при качении без скольжения

Работа сил трения, действующих  на   катя­щееся тело. На колесо ра­диуса R (рис.28), катящееся по некоторой плоскости (поверх­ности) без скольжения, действует сила трения F , препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы  . Но точка В в данном случае является мгновенным центром скоростей и  . Так как  , то   и для каждого элементарного перемещения  .

Следовательно, при качении без скольжения, работа силы тре­ния, препятствующей скольжению, на любом перемещении тела равна нулю.По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.28,а).

Сопротивление качению, возникающее вследствие деформации поверх­ностей (pис.28,б), создает пару ( ), момент которой  , где k-коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса  , получим:

,

где  - элементарное перемещение центра С колеса.

Если N= const, то полная работа сил сопротивления качению будет равна

Так как величина   мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.