Кинетическая энергия тела при различных видах его движения

Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки 

или

Таким образом, кинетическая энергия тела при поступатель­ном движении равна половине произведения массы тела на квад­рат скорости центра масс. От направления движения значение Т не зависит.

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рнс.25), то скорость любой его точки  , где  - расстояние точки от оси вращения, а - угло­вая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:

Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:

т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.

 

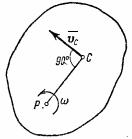
3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (рис.26). Следовательно ,где  - момент инерции тела относительно названной выше оси, - угловая скорость тела. Величина   в формуле будет перемен­ной, так как положение центра Р при движе­нии тела все время меняется. Введем вместо   постоянный момент инерции  , относительно оси, проходящей через центр масс С тела.  По теореме Гюйгенса  , где d=PC. Подставим это выражение для  . Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно,  , где  - скорость центра масс С, окончательно найдем:

.

Следовательно, при плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной с кинетической энергией вращательного движения вокруг центра масс.

Выражение кол-ва движения системы через ее массу и скорость центра масс

количество движения равно произведению массы (величина, характеризующая инертность тела при поступательном движении) на скорость

Кинетический момент вращающегося тела относительно оси вращения

кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то, очевидно, будет

Легко видеть аналогию между формулами  и  : количество движения равно произведению массы (величина, характеризующая инертность тела при поступательном движении) на скорость; кинети­ческий момент равен произведению момента инерции (величина, характеризующая инертность тела при вращательном движении) на угловую скорость.