2.1. Показатели безотказности объекта.

Безотказность [2] – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.

Наработка [28] - продолжительность или объем работы. Наработка неразрывно связана с понятием «отказ». Появление отказов (вероятность) исчерпывающе описывается законами распределения случайных величин, а для оперативных оценок – моментами СВ. Наиболее полно изучены методы оценки появления отказов – не связанные со строением элементов.

2.1.1. Вероятность безотказной работы.

[35] – вероятность того, что в пределах заданной наработки отказ не возникнет. Вероятность отказа и вероятность безотказной работы всегда образуют полную группу событий: .

Вероятность отказа , где n(t) – число отказов в интервале [0;t], N₀ – число наблюдаемых объектов.

, - рубеж, при котором вычисляется отказ при t=0, q(t)=0

t=, q(t)=1.

q(t) описывается интегральным законом распределения этой величины

q (t₁;t₂)=q(t₂)-q(t₁)

p(t) – вероятность безотказной работы:

- число отказов до t.

- вероятность того, что не откажет на интервале [0; ].

Совместное наступление событий А и В  Р(А В)=Р(А)  Р_А(В)

2.1.2. Частота отказов f(t) – отношение числа отказавших элементов в некотором интервале t к первоначальному числу отказавших элементов.

, где t – начало интервала измерения.

Определим связь между f(t), P(t), q(t).

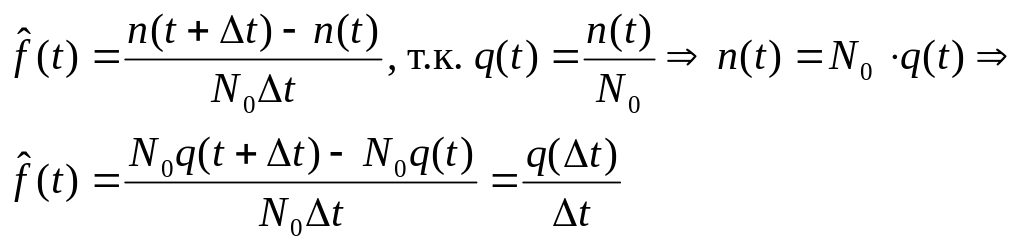
при t0

! ; т.е. соотношение интегрирования и дифференцирования.

!

1 этап – область проработки

2 этап – область нормальной эксплуатации объекта

3 этап – старение (износ) и интенсивные отказы.

2.1.3. Интенсивность отказов [39].

(t) – условная плотность вероятности возникновения отказов невосстанавливаемых объектов, определенная для рассматриваемого момента времени t, при условии, что до этого момента отказ не возникал.

при t0

2.1.4. Закон надежности – зависимость вероятностей от f.

Определить зависимость P(t) от .

- табличное f 

при начальных условиях с=0.

Из выражения (1) , что

при

2.1.5. Средняя наработка до отказа [36] – математическое ожидание этой наработки.

Определение взаимн. t₀ и P(t)

беря по частям:

06.11.02г

[36] -%-я наработка до отказа – наработка, в течение которой отказ не возникает с вероятностью , выраженной в %

t_--% наработка;

 - вероятность, выраженная в %.

, при экспоненциальном законе распределения (=const).

Примеры простейших постановок надежности.

I. Определить вероятность безотказной работы за 100 часов наработки при интенсивности отказов 25010^{-6 1}/_ч.

• Закон е-й 

Р(100)=

II. Определить интенсивность отказа устройства, обеспечивающего 10 часов наработки до отказа с вероятностью 0,999.

• Примем экспоненциальный закон надежности

III. Определить наработку дисковода, достигнутую с вероятностью 0,99; 0,999; 0,9999.

При рекламе среднего времени наработки на отказ 28 лет (250 000 часов).

При е-м законе распределения определяем нагрузку до отказа:

IV. Прогнозирование надежности. Используя подтвержденную наработку устройства = 1000 часов с вероятностью 0,99. Какова вероятность безотказной работы его за 10000часов. При е-м законе распределения

V. Определить -% медианную наработку на контакт разъема при интенсивности отказа контакта =610^{-6 1}/_ч.