
- •1. Канонические уравнения для расчета статически неопределимых систем.
- •2. Порядок расчета статически неопределимых систем при изгибе
- •3.Расчет статически неопределимых систем при изгибе. Выбор основной системы.
- •4. Определение перемещений в статически неопределимых системах
- •5.Общие принципы расчета конструкций при сложном сопротивлении
- •6.Косой изгиб. Определение положения нейтральной оси.
- •7.Косой изгиб. Определение напряжений
- •8.Косой изгиб. Определение деформаций.
- •9.Внецентренное растяжение и сжатие. Определение напряжений.
- •10. Внецентренное растяжение и сжатие. Определение положения нейтральной оси.
- •11. Ядро сечения
- •12. Построение эпюр крутящих моментов.
- •13.Кручение с изгибом
- •14. Анализ напряженного состояния при кручении с изгибом.
- •15. Понятие расчета на устойчивость.
- •16. Критическая сила. Критические напряжения. Условие устойчивости.
- •17. Влияние условий закрепления на величину критической силы.
- •18.Предел применимости формулы Эйлера.
- •19. Определение критических напряжений по формуле Ясинского.
- •32. Кривая усталости при симметричном цикле.
- •33. Понятие о пределе выносливости.
- •34. Диаграмма предельных амплитуд.
7.Косой изгиб. Определение напряжений
Косой изгиб возникает в брусе в том случае, когда плоскость действия суммарного изгибающего момента не совпадает с главными центральными осями поперечного сечения бруса.
Сила F лежит в плоскости поперечного сечения и проходит через центр тяжести.
Рассмотрим сечение, с центром тяжести совместим систему координат.
1. Напряжение:
- Используя принцип независимости действия сил, расчеты при косом изгибе удобнее представить как сумму результатов изгибов в 2х плоскостях.
Для этого раскладываем силу F на проекции. Каждая из этих проекций вызывает изгиб.
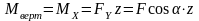
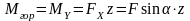
Если рассматривать в сечении точку К с координатами (XK, YK), то напряжение в этой точке можно представить как сумму напряжений от изгибов в этой горизонтальной и вертикальной плоскости.

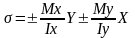 - формула для определения напряжений
при косом изгибе.
- формула для определения напряжений
при косом изгибе.
Х, У – координаты точки, в которой определяем напряжение.
Ix, Iy – моменты инерции.
«+» - если волокна, проходящие через точку растянуты.
«-» - если сжаты.
 - условие прочности при косом изгибе.
- условие прочности при косом изгибе.
8.Косой изгиб. Определение деформаций.
Косой изгиб возникает в брусе в том случае, когда плоскость действия суммарного изгибающего момента не совпадает с главными центральными осями поперечного сечения бруса.
Сила F лежит в плоскости поперечного сечения и проходит через центр тяжести. При изгибе деформация в поперечном сечении стержня определяется перемещением у центра масс сечения в направлении, перпендикулярном первоначальному положению оси стержня, называемым прогибом и углом поворота и сечения по отношению к своему первоначальному положению. Для нахождения деформаций во всех поперечных сечениях по длине стержня необходимо получить зависимости у = y(x) и и = и(x). Первую называют уравнением изогнутой оси или уравнением прогибов. Касательная к изогнутой оси стержня в любой ее точке составит с первоначальной осью угол, равный углу поворота и сечения в данной точке. Тангенс угла и наклона касательной tg и = dy/dx. Но так как фактические значения углов поворота поперечных сечений при изгибе малы, порядка тысячных долей радиана, можно тангенс угла приравнять значению угла (tgи ? и) и найти связь между углом поворота сечения и прогибом в виде зависимости и ? ? dy/dx.
9.Внецентренное растяжение и сжатие. Определение напряжений.
Таким образом, при внецентренном растяжении-сжатии возникает 3 внутренних силовых фактора – продольная сила и 2 изгибающих момента. Рассмотрим произвольное сечение с координатой z. Пометим в этом сечении т. К (XK, YK)
Определим напряжение в точке К:
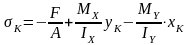
По данной формуле можно рассчитывать напряжение в любой точке.
МХ и МУ от координаты Z не зависит.
Определим max напряжение в поперечном сечении:
Согласно предыдущей формуле:
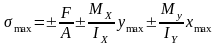
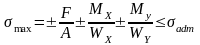 - условие прочности при внецентренном
растяжении (сжатии).
- условие прочности при внецентренном
растяжении (сжатии).
+ - растяжение волокон
- - сжатие.
10. Внецентренное растяжение и сжатие. Определение положения нейтральной оси.
Выберем точку N (Хn, Yn) таким образом, чтобы в формуле напряжений все три слагаемых были с одинаковым знаком и предположим, что эта точка принадлежит нейтральной линии сечения.
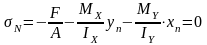
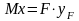 ;
;
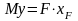 ч
ч
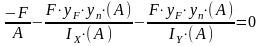
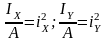 - радиусы инерции относительно осей Х
и У.
- радиусы инерции относительно осей Х
и У.
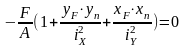
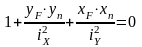 - уравнение нейтральной линии при
внецентренном растяжении(сжатии).
- уравнение нейтральной линии при
внецентренном растяжении(сжатии).
Выводы:
1. Xn, Yn – входят в уравнение первой степени, то это уравнение прямой.
2. 1-е слагаемое в уравнении «1» указывает на то, что при внецентренном растяжении (сжатии) нейтральная линия никогда не пройдет через центр тяжести сечения.
3. Если линия действия нагрузки пересекает координатную ось, то в формуле напряжений также как и в уравнении нейтральной линии выпадает одно из слагаемых.
В практических расчетах положение нейтральной линии удобно определять через отрезки, которые она отсекает на координатных осях
