6.Теоремы о сочетании элементов симметрии

• 1. Осевая теорема Эйлера - Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

• Частные случаи:

• 1) если есть поворотная ось симметрии порядка n и перпендикулярно этой оси проходит поворотная ось 2-го порядка, то всего имеется n осей 2-го порядка;

• 2) если под углом a пресекаются две поворотные оси 2-го порядка, то перпендикулярно им проходит поворотная ось с элементарным углом поворота в 2 раза большим угла пересечения (2a).

• 2. Точка пересечения оси симметрии второго порядка (L2) или четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии. Обратная теорема: Если есть центр симметрии и через него проходит плоскость симметрии, то перпендикулярно этой плоскости через центр симметрии проходит двойная ось симметрии.

• 3. Линия пересечения двух плоскостей симметрии является осью симметрии, причем, угол поворота вокруг оси вдвое больше угла между плоскостями. Следствия: 1) в присутствии оси симметрии порядка n и плоскости, проходящей вдоль оси, всего имеем n таких плоскостей;

• 2) Плоскость, проходящая вдоль инверсионной оси симметрии 3-его и 4-го порядков, приводит к появлению оси 2-го порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.

7.Принцип вывода 32 классов симметрии

Р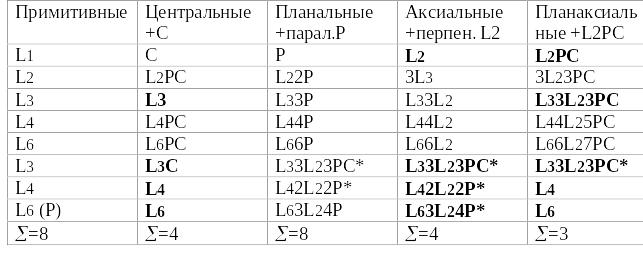 усский кристаллограф А.В. Гадолин в 19 в математически доказал, что в кристаллических многогранниках, тело которых строго ограниченно и зависит от внутреннего строения кристаллов, элементы симметрии наблюдаются в определенных комбинациях. Таких комбинаций элементов 32. Их назвали классами, или видами симметрии. Разделение кристаллов на 32 класса лежит в основе классификации геометрических форм кристаллов.

8.Сингонии и категории, их характеристика

• 32 класса симметрии подразделяются на 3 категории

(низшую, среднюю и высшую ) и 7 (6) сингоний

Категория	Сингония	Символы и названия классов
		Примитивный	Центральный	планальный	аксиальный	планаксиальный	инверсионно-примитивный	инверсионно-планальный
Низшая	Триклинная	L1 1	C 1
	Моноклинная			P m=2	L2 2	L2PC 2/m
	Ромбическая			L22P mm2=mm	3L2 222	3L23PC mmm
Средняя	Тригональная	L3 3	L3C=L3i 3	L33P 3m	L33L2 32	L33L23PC 3m=32/m
	Тетрагональная	L4 4	L4PC 4/m	L44P 4mm=4m	L44L2 422	L44L25PC 4/mmm	L4iL2 4	L4i2L22P 42m
	Гексагональная	L6 6	L6PC 6/m	L66P 6mm	L66L2 622	L66L27PC 6/mmm	L3P=L6i 6	L6i3L23P=L33L24P 6m2=62m
Высшая	Кубическая	3L24L3 23	3L24L33PC m3=2/m3	3L2 (3L4i) 4L36P 43m	3L4 4L36L2 432	3L4 4L3 6L29PC m3m
	Курсив - инверсионные оси	Оси полярные	Оси неполярные	Оси полярные	Полярные L2	Оси неполярные

• В сингонию (сходноугольность) объединяются те кристаллы, для которых одинакова симметрия элементарных ячеек их структур и одинакова система координат. В сингониях одинаковое количество единичных направлений: в низших – не менее 3-х, в средних – одно, в высшей – нет.