Вопрос 23. Асимптоты функции.

Определение: Прямая 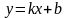называется наклонной асимптотой функции f(x) при 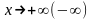, если f определена в окрестности точки 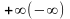и расстояние между графиком и прямой стремится к нулю.

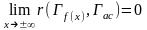
Уравнение наклонной асимптоты:

Пусть - асимптота при

, , ,

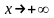
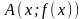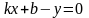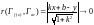
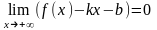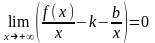, , , значит ,

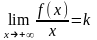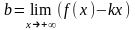
Замечание: возможен случай, когда k существует, а b – нет, в этом случае асимптот нет!

Вопрос 24. Первообразная. Теорема о первообразной.

Определение 1: Функция F называется первообразной функции f на интервале (a,b), если функция f непрерывна на интервале (a,b), и для всех x из этого интервала выполняется равенство: F΄(x)=f(x).

Замечание: Вместо (a,b) можно рассматривать [a,b], (a,b] и [a,b), но нужно будет говорить про односторонние производные: 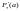=f(a), и =f(b).

Пример

.

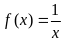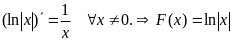
на промежутке (-∞,0) и на (0,+∞).

Теорема:(О множестве всех первообразных).

Пусть F(x) является первообразной функции f(x) на на промежутке I, тогда функции вида F(x)+C и только они являются первообразными функции f(x), где C – произвольная константа.

Доказательство:

Пусть функция F(x) – первообразная функции f(x), тогда F΄(x)=f(x) и (F(x)+C)΄=f(x). Пусть функции F и G – первообразные функции f(x) на промежутке I (нужно доказать, что они отличаются на константу). Тогда (F-G)΄=0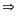 F-G=C (по теореме о функции, имеющей нулевую производную).

Теорема доказана.

Свойства первообразных.

1. Пусть функция f(x) имеет первообразную F(x) на промежутке I и функция g(x) имеет первообразную G(x) на промежутке I, тогда функция f(x)±g(x) будет иметь первообразную F(x)±G(x) на промежутке I.

2. Первообразной функции k·f(x) является функция k·F(x).

3. Первообразной производной функции f΄(x) является сама функция f(x).

Вопрос 25. Неопределенный интеграл. Его свойства.

Определение 1: Множество всех первообразных функции f(x) на промежутке I называется неопределенным интегралом и обозначается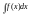 . При этом если функция F(x) – первообразная функции f(x), то .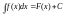

Пример:

.

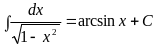Свойства неопределенного интеграла.

1. .

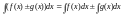Замечание: Обратное неверно! Из существования интеграла 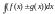не следует существование интегралов и .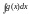

.

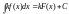2. .

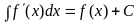3. 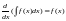(по определению).

Вопрос 26. Метод внесения под знак дифференциала. Метод подстановки.

Теорема (замена переменной в неопределенном интеграле):

Пусть функция 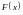является первообразной для функции на некотором промежутке 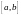и функция 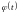непрерывная и имеет непрерывную производную на промежутке 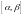, причем для всякого значения 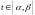выполняется неравенство 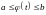. Тогда будет справедлива формула:

(*),

где .

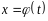Формулу (*) можно применять, не вводя явно новой переменной. В общем виде она будет выглядеть следующим образом: . Тогда, если 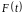- первообразная функции 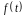, то . Такой прием называют внесением под знак дифференциала.

Основную роль в интегральном исчислении играет формула замены переменных (или подстановки) 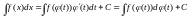(1).

В этой формуле предполагается, что есть непрерывно дифференцируемая функция на некотором интервале изменения , а - непрерывная функция на соответствующем интервале или отрезке оси . Докажем это утверждение. Слева в (1) стоит функция, которая является первообразной от . Ее производная по равна:

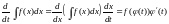
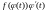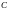Следовательно, если ввести в этой функции подстановку , то получится первообразная от функции . Интеграл же справа есть, по определению, некоторая первообразная от . Но две первообразные для одной и той же функции отличаются на некоторую постоянную . Это и записано в виде первого равенства (1). Что касается второго, то оно носит формальный характер - мы просто уславливаемся писать:

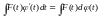
Пример: .
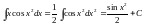