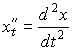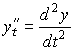Вопрос 7. Производная сложной функции.
Теорема:
Пусть
функция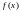
такая, что
,
и функция
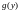такая,
что
,
.
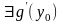Тогда функция
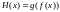и
.
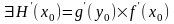Доказательство:
дифференцируема
в точке
,
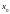тогда:
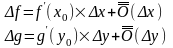
Рассмотрим ∆H:
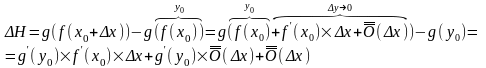
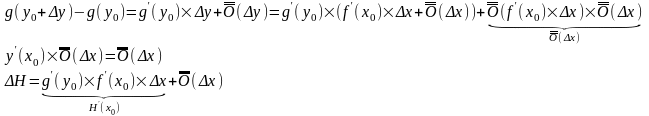
Вопрос 8. Производная высших порядков. Дифференциал высших порядков.
Пусть
функция y=f(x)
дифференцируема в точке Xo,
то есть существует ее производная в
этой точке f
’ (Xo).
Пусть f
- дифференцируема в некоторой окрестности
U(Xo).
f’(x)
определена на U(Xo)
и если дифференцируема в точке Xo,
то (f’(Xo))’=f’’(Xo).
Вообще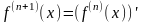
Теорема: (Формула Лейбница)
Пусть
функции U
и V
n
раз дифференцируемы, т.е. существуют
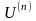и
.
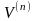Значит (U*V)
– тоже n
раз дифференцируема, при этом
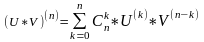
Доказательство:
Метод математической индукции:
Пусть при n=m – верно, т.е.
(*)
Надо доказать, что
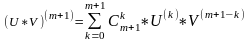
Доказательство:
Теорема доказана.
f(x)
дифференцируема,
тогда
.
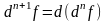Далее, пусть f
– n
раз
дифференцируема,
__________________________
.
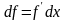
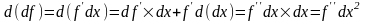
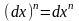Докажем, что
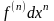
1)
,
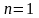2)
Пусть при n
= m
3)
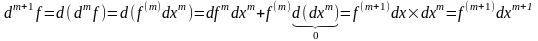
Инвариантность/Неинвариантность.
1)
y(x),
x
– независимая
переменная,
,
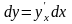пусть x
= x(t)
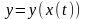
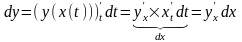
2)
y(x),
x
– независимая
переменная,
,
,
,
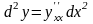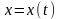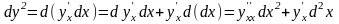здесь
,
.
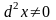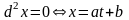Вопрос 9. Дифференцирование параметрически заданной функции.
До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений
где t -
вспомогательная переменная,
называемая параметром.
Заметим,
что функция может быть представлена в
параметрической форме различными
способами.
Например, функция,
записанная в неявном виде x2 + y2 =
1 может быть представлена в явном
виде: 
и
в параметрической форм е:
Заметим, что x2 + y2 = 1 есть уравнение окружности единичного радиуса с центром в начале координат. В первом параметрическом представлении уравнения x2 + y2 = 1 параметр t изменяется от -1 до +1 и равен абциссе подвижной точки окружности, во втором случае параметр t изменяется от 0 до 2p и равен углу, образованному радиусом подвижной точки и осью Ox. Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме
От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=j (y), так как уравнение F(x,y)=0 может оказаться неразрешимым_относительно y или x . Легко перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найти t=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)
y=y[t(x)]=f(x)
От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно. Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения
и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0. Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если
y(t)=f [ x(t) ].
Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как_функцию_от x._То_есть t=t(x).Тогда y=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле
и применим формулу, связывающую производные обратных функций:
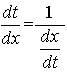
Введя обозначения
,
получим
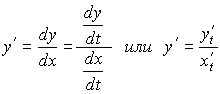
Пример.
Теперь найдем вторую производную от функции, заданной в параметрической форме. Из предыдущего уравнения и определения второй производной следует, что
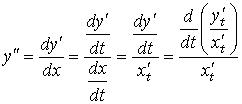
но
Следовательно
где
