
- •Вопрос 1. Определение производной, ее геометрический смысл.
- •Вопрос 2. Непрерывность функции, имеющей производную.
- •Вопрос 3. Производная суммы, произведения, частного.
- •Вопрос 4. Производная обратной функции.
- •Вопрос 5. Определение дифференцируемости функции. Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Вопрос 6. Дифференциал. Его геометрический смысл.
- •Вопрос 7. Производная сложной функции.
- •Вопрос 8. Производная высших порядков. Дифференциал высших порядков.
- •Вопрос 9. Дифференцирование параметрически заданной функции.
- •Вопрос 10. Теорема Ферма. Ее геометрический смысл.
- •Вопрос 11 Теорема Ролля. Ее геометрический смысл.
- •Вопрос 13. Теорема о среднем Лагранжа. Ее геометрический смысл.
- •Вопрос 14. Правило Лопиталя. Раскрытие неопределенностей. Правило Лопиталя. Случай 0/0.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида , , , , .
- •Вопрос 15. Разложение многочлена по степеням (х-а)
- •Вопрос 16. Формула Тейлора с остаточным членом в форме Лагранжа.
- •Вопрос 17. Остаточный член в форме Пеано.
- •Вопрос 18. Ряд Тейлора, его сходимость, признак сходимости.
- •Вопрос 19.
- •Экстремум функции. Необходимое условие экстремума непрерывной функции.
- •Вопрос 20. Экстремум функции. Достаточное условие экстремума непрерывной функции.
- •Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
- •Вопрос 21. Достаточное условие экстремума функции, имеющей n-ную производную.
- •Вопрос 22.
- •Выпуклость и вогнутость прямой. Точки перегиба.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Вопрос 23. Асимптоты функции.
- •Вопрос 24. Первообразная. Теорема о первообразной.
- •Вопрос 25. Неопределенный интеграл. Его свойства.
- •Вопрос 26. Метод внесения под знак дифференциала. Метод подстановки.
- •Вопрос 27. Интегрирование по частям.
- •Вопрос 28. Интегрирование рациональных дробей.
- •Вопрос 30.
- •Интегрирование тригонометрических функций.
- •Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
- •Вопрос 32. Необходимое условие интегрируемости.
- •Вопрос 33. Суммы Дарбу. Их свойства.
- •Вопрос 34. Необходимое и достаточное условия интегрируемости функции.
- •Вопрос 35. Достаточное условие интегрируемости функции.
- •Вопрос 36. Свойства определенного интеграла.
- •Вопрос 37. Интеграл с переменным верхним пределом, его непрерывность.
- •Вопрос 38. Дифференцируемость интеграла с переменным верхним пределом.
- •Вопрос 39. Формула Ньютона-Лейбница.
- •Вопрос 40. Замена переменной в определенном интеграле.
- •Вопрос 41. Интегрирование по частям определенного интеграла.
- •Вопрос 42. Теорема о среднем для определенного интеграла.
- •Вопрос 43. Непрерывная и гладкая прямая, заданная параметрически. Длина этой кривой.
- •Вопрос 44. Площадь фигуры, заданной в полярной системе координат.
- •Вопрос 45. Объем тел вращения.
Вопрос 41. Интегрирование по частям определенного интеграла.
Интегрирование по частям — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы для определённого интеграла:
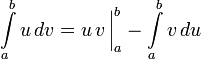
Предполагается,
что нахождение интеграла ![]() проще,
чем
проще,
чем ![]() .
В противном случае применение метода
не оправданно.
.
В противном случае применение метода
не оправданно.
Пример:
![]()
Вопрос 42. Теорема о среднем для определенного интеграла.
Теорема о среднем
Пусть
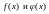 интегрируемы
на
,
причем
интегрируемы
на
,
причем
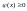 на данном промежутке, тогда
на данном промежутке, тогда
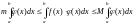 ,
где
,
где
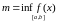 ,
,
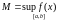
и
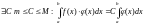
Замечание: sup и inf существуют, т.к. функция на данном промежутке интегрируема, а значит ограничена.
Доказательство:
Запишем
неравенство:
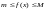 и домножим его на
и домножим его на
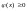 :
:
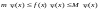 ;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
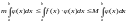 (
( )
)
Если
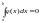 ,
то и интеграл
,
то и интеграл
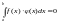 и неравенство (
)
выполняется.
и неравенство (
)
выполняется.
Если
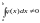 ,
тогда по теореме о неравенствах
,
тогда по теореме о неравенствах
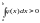 ,
значит можно неравенство (
)
на него разделить:
,
значит можно неравенство (
)
на него разделить:
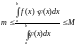 и
принимаем за
и
принимаем за
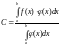 .
Теорема доказана.
.
Теорема доказана.
Вопрос 43. Непрерывная и гладкая прямая, заданная параметрически. Длина этой кривой.
Пусть l —
гладкая, спрямляемая кривая, заданная
параметрически (![]() —
касательный вектор кривой l. Пусть
также функция
—
касательный вектор кривой l. Пусть
также функция ![]() и
вектор-функция
и
вектор-функция ![]() определены
и интегрируемы вдоль кривой l в
смысле криволинейного интеграла второго
рода. Тогда
определены
и интегрируемы вдоль кривой l в
смысле криволинейного интеграла второго
рода. Тогда
![]()
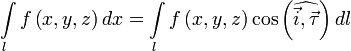
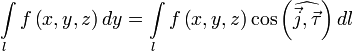
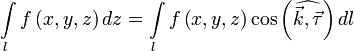
Вопрос 44. Площадь фигуры, заданной в полярной системе координат.
П
 усть
множество задано в полярных координатах:
x=r·cost,
y=r·sint.
Рассмотрим множество A,
такое, что α≤t≤β
и 0≤r≤r(t).
Введем разбиение угла [α,β]:
α=t0<t1<t2<…<tn=β.
При этом Δti=[ti
,ti+1].
Рассмотрим сектора окружностей ri=mi
– это будут сектора
усть
множество задано в полярных координатах:
x=r·cost,
y=r·sint.
Рассмотрим множество A,
такое, что α≤t≤β
и 0≤r≤r(t).
Введем разбиение угла [α,β]:
α=t0<t1<t2<…<tn=β.
При этом Δti=[ti
,ti+1].
Рассмотрим сектора окружностей ri=mi
– это будут сектора
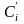 и ri=Mi
– это будут сектора
и ri=Mi
– это будут сектора
 .
.
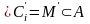 и
и
 .
Окружности (с углом 2π) соответствует
площадь πR2,
а сектору с углом α – площадь αR2/2.
Поэтому
.
Окружности (с углом 2π) соответствует
площадь πR2,
а сектору с углом α – площадь αR2/2.
Поэтому
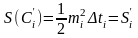 и
и
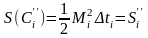 .
.
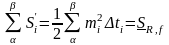 и
и
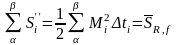 -
нижняя и верхняя суммы Дарбý для функции
f=r2/2.
Получим
-
нижняя и верхняя суммы Дарбý для функции
f=r2/2.
Получим
 и
и
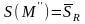 .
То есть площадь S(A)
существует и равна S
(т.е. A квадрируема)
тогда и только тогда, когда существует
интеграл
.
То есть площадь S(A)
существует и равна S
(т.е. A квадрируема)
тогда и только тогда, когда существует
интеграл
 .
.
Вопрос 45. Объем тел вращения.

Рассмотрим вращение произвольное тело вращения.
Пусть
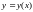 -
есть произвольная непрерывная функция,
причем
-
есть произвольная непрерывная функция,
причем
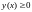 на отрезке
.
Будем вращать данную кривую на отрезке
вокруг оси
на отрезке
.
Будем вращать данную кривую на отрезке
вокруг оси
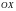 .
Получим тело вращения
.
Получим тело вращения
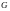 .
.
Разобьем
отрезок
:
![]() .
Пусть
.
Пусть
 ,
,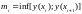 .
Рассмотрим два цилиндра
.
Рассмотрим два цилиндра
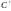 и
и
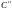 (см.
рис. )
(см.
рис. )
 ,
,
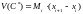 .
Теперь пусть
.
Теперь пусть
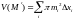 и
и
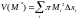 .
Нетрудно видеть , что
.
Нетрудно видеть , что
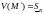
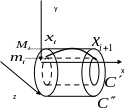 и
и
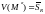 .
Это означает, что если функция
.
Это означает, что если функция
 интегрируема на отрезке
,
то
интегрируема на отрезке
,
то
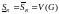 и
и
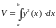 .
При вращении вокруг оси
.
При вращении вокруг оси
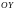 формула примет вид
формула примет вид
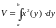 .
.
Пример: Рассмотрим вычисление объема тела вращения на примере шара:
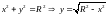 .
Значит объем шара равен:
.
Значит объем шара равен:
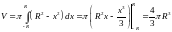 .
.
